A car took 5 hours to travel from town A to town B. A bus took 9 hrs to travel the same route. both the car and bus started at the same time. if the speed of the car was 90km/h, how much faster did the bus need to travel in order to reach town B 1hr and 36 min earlier than the expected arrival time. if it could only increase it's speed after 3/5 of the journey?
Since car takes 5 hours to reach B, @ 90 km/h, distance from A to B = 5(90) = 450 km
Since bus takes 5 hours to reach B, a distance of 450 km, the bus' speed = 
Travelling  of the distance, the bus must travel
of the distance, the bus must travel 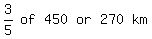 . This means that the bus needs to travel another 180 (450 - 270) km to get to B
. This means that the bus needs to travel another 180 (450 - 270) km to get to B
The bus traveled 270 km from A, in  . Therefore, it needed another
. Therefore, it needed another 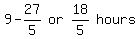 to get to B on time
to get to B on time
However, since it'd need to get to B  sooner, then it'd need to travel for
sooner, then it'd need to travel for 
Traveling the remaining 180 km to B, in 2 hours means that the bus would need to travel at a speed of 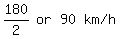
Hence, the bus would need to travel 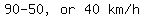 more to get to B, 1 hour and 36 minutes earlier than planned.
more to get to B, 1 hour and 36 minutes earlier than planned.