Question 1161622: A person plans to invest a total of $250,000 in a money market account, a bond fund, an international stock fund, and a domestic stock fund. She wants 60% of her investment to be conservative (money market and bonds). She wants the amount in domestic stocks to be 4 times the amount in international stocks. Finally, she needs an annual return of $10,000
Assuming she gets annual returns of 2.5% on the money market account, 3.5% on the bond fund, 4% on the international stock fund, and 6% on the domestic stock fund, how much should she put in each investment?
Answer by ikleyn(52818)   (Show Source):
You can put this solution on YOUR website! .
60% of $250000, i.e. $150000, go to the money market and bonds.
Hence, 40%, or $100000, go to the international and domestic funds.
These $100000 splits this way: $820000 go to the international and $80000 to the domestic.
Then these $100000 produce the annual interest of 0.04*20000 + 0.06*80000 = 5600 dollars.
Thus you reduce the problem to TWO funds ONLY: a money market account and the bond fund
with the total amount of $250000 - $100000 = $150000 and the annual interest of $1000 - $5600 = $4400.
It can be solved using one unknown x = bonds. You have then this equation
0.025*(150000-x) + 0.035*x = 4400
The solution to it is
x = 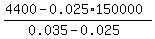 = 65000 dollars.
ANSWER. Bonds: $65000; money market: 150-65000 = 85000 dollars;
international: $20000; domestic: $80000.
Solved, answered, explained and completed.
|
|
|
