Question 1144732: The coordinates of points A, B, and C are A(-4,9), B(k,0), and C(8,3). What is the value of k, which causes the sum AB+BC to be as small as possible?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website! AB+BC is smallest when A, B, and C are collinear (lie on the same straight line).
Use any of a number of methods to find the value of k that makes the three points collinear.
I prefer logical reasoning, using an UNDERSTANDING of the slope of a line, along with simple arithmetic, over formal algebra where it is practical, as it is in this problem.
From A to C is 12 to the right and 6 down, for a ratio of 2 to the right and 1 down. (A slope of -1/2, if you prefer.) To get y from 3 at point C to 0, I need to go down 3, which means I need to go right 6; so the value of k is 8+6 = 14.
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
As the problem is formulated, it is not exactly clear what this sum, AB + BC, means.
I will interpret it as the sum of the lengths of segments AB and BC.
My solution is different from the solution by the tutor @greenestamps, and gives another answer.
It is a version of the classic Fermat's problem :
on the plane, a straight line L and two points A and C are given in the same of the two half-planes.
Find the shortest path from A to C under the imposed condition, that this path must touch the line L at some point B.
In our case the points are two given points A and C; the straight line L is the x-axis,
and we are searching for the point B on this line (on this x-axis)
The solution (very well and widely known) is THIS :
- take the point C; reflect it symmetrically about x-axis to get its mirror image C';
- then connect the point A with C' by a straight line (which is unique);
- its intersection with x-axis will be the point B, you are looking for.
So, everything is very easy.
- The mirror image of the pont C(8,3) is the point C'(8,-3);
- the straight line connecting A(-4,9) with C'(8,-3) has the slope m =  =  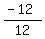= -1;
- the equation of this straight line is y = 9 - 1*(x-(-4) = 9 - (x+4) = -x + 5;
- its intersection with the x-aqxis is at x = 5 (x-intercept);
- therefore, the point B has coordinates B = (5,0);
- hence, k = 5 is the ANSWER to the problem's question.
Answered, solved, explained in all details and completed.
-----------------
As I presented here this solution for you, it is, usually, one full-scale session of a school Math circle.
So, it is as if you visited a first-class school Math circle today at a local University . . .
|
|
|
