Question 1139774: Colton's parents want to create a college fund that pays $2,600.00 paid at the end of each quarter for 5 years, if interest is earned at a rate of 5%, compounded quarterly, how much needs to be invested now for this to happen.
Colton's parents need to invest $________
Found 3 solutions by josmiceli, MathTherapy, greenestamps:
Answer by josmiceli(19441)   (Show Source):
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website!
Colton's parents want to create a college fund that pays $2,600.00 paid at the end of each quarter for 5 years, if interest is earned at a rate of 5%, compounded quarterly, how much needs to be invested now for this to happen.
Colton's parents need to invest $________
You're looking for the amount to invest "today" in order to receive $2,600 every quarter for 5 years, and compounded at 5% per year.
The other person's answer is WRONG!! Therefore, IGNORE his answer.
This works the same way as purchasing a property for a certain price and then making monthly payments. However, in this case, the periodic payments to you would be made every quarter.
You then use the formula for the present value of an ordinary annuity, or:  , where:  .
To realize your goal of receiving $2,600 per quarter for 5 years, @ an interest rate of 5% per annum, you need to invest  .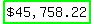
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
(1) The solution by the other tutor tells how much you need to invest at 5% compounded quarterly to have the lump sum of 20*$2600 = $52000 at the end of 5 years. Since the fund is supposed to provide distributions of $2600 each quarter for 20 quarters, that is clearly not the answer you are looking for.
(2) From the wording of the problem, it appears as though the parents want to make the lump sum investment at the beginning of the 5 years during which the distributions are to be made. That is not the usual way it is done; usually the investment is made long before the beginning of those 5 years.
Re-post the problem, making it clear in your statement of the problem when the initial investment is made.
|
|
|
