Question 1124483: An urn contains five red balls, two green balls, and three yellow balls. Three balls will be drawn from the urn, one at a time, at random.
If the balls are drawn without replacement (i.e. when a ball is drawn it is not placed back into the urn before the next draw), what is the probability the first is yellow, the second is green, and the third is red?
If the balls are drawn with replacement (i.e. when a ball is drawn it is placed back into the urn before the next draw), what is the probability the first is yellow, the second is green, and the third is red?
Enter your answers as whole numbers or fractions in lowest terms.
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! a)
1st draw: P(Y) = 3/(5+2+3) = 3/10
2nd draw: P(G) = 2/(5+2+2) = 2/9
3rd draw: P(R) = 5/(5+1+2) = 5/8
( each denominator is R+G+Y remaining in the urn )
P(Y, G, R) = (3/10)*(2/9)*(5/8) = 30/720 = 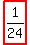
b)
In this case, the number of each color stays fixed (5,2,3 for R,G,Y, respectively), and the denominator obviously stays fixed at 10:
P(Y, G, R) = (3/10)*(2/10)*(5/10) = 30/1000 = 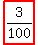
---
EDITED 9/27: Fixed the with-replacement calculation. I had 3*2*3/1000 when it should have been 3*2*5/1000. Sorry. Corrected version is above.
|
|
|