Question 1120925: The roots z1,z2 Nd z3 of the equation x^3+3ax^2+3bx+c=0 in which a,b and c are complex numbers, correspond to the points A,B and C on the Argand plane. Find the C.G. of ∆ABC and show that it will be equilateral if a^2=b
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the C.G. of ∆ABC
C.G. of a triangle is the center of gravity of the triangle.
The center of gravity of the triangle with the vertices A, B and C is the point with coordinates
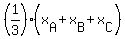 and and 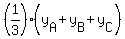 .
Geometrically, this point is nothing else as .
Geometrically, this point is nothing else as  .
According to Vieta's theorem, the sum .
According to Vieta's theorem, the sum 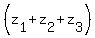 is the coefficient at x^2 of the given equation with the opposite sign, i.e. -3a.
Thus the center of gravity of the given triangle is the complex number -a. is the coefficient at x^2 of the given equation with the opposite sign, i.e. -3a.
Thus the center of gravity of the given triangle is the complex number -a.
Show that it will be equilateral if a^2 = b
If a^2 = b, then the given equation
x^3 + 3ax^2 + 3bx + c = 0
becomes
x^3 + 3ax^2 + 3a^2*x + c = 0, or, equivalently,
(x^3 + 3ax^3 + 3a^2*x + a^3) + (c-a^3) = 0,
(x+a)^3 = -(c-a^3),
x + a = 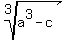 ,
x = - a + ,
x = - a + 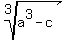 . (1)
If you are familiar with the basics of complex number theory, you will recognize that the formula (1)
describes the three complex numbers around the point "-a" (the center of gravity of the triangle ABC) turned at the angle 120 degrees
one relative the other.
So the triangle ABC is an equilateral triangle. . (1)
If you are familiar with the basics of complex number theory, you will recognize that the formula (1)
describes the three complex numbers around the point "-a" (the center of gravity of the triangle ABC) turned at the angle 120 degrees
one relative the other.
So the triangle ABC is an equilateral triangle.
Regarding the basics of complex number theory, you have the set of lessons
- Complex numbers and arithmetical operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Raising a complex number to an integer power
- How to take a root of a complex number
- Solution of the quadratic equation with real coefficients on complex domain
- How to take a square root of a complex number
- Solution of the quadratic equation with complex coefficients on complex domain
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Complex numbers".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|