Question 1065915: In ΔABC, m∠ACB = 90°,
CD ⊥ AB and m∠ACD = 45°. Find:
Find AC, if CD = 6(root)2 in.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  m∠ACB = 90° tells us that ABC is a right triangle.
CD ⊥ AB tells us that ACD and BCD are right triangles too.
In other words, m∠ADC = 90° and m∠BDC = 90°.
m∠ACD = 45°, together with m∠ADC = 90°,
tells us that m∠DAC = 90° - 45° = 45° .
So ADC is an isosceles right triangle,
with two congruent 45° base angles,
and two congruent legs, measuring  .
In every isosceles right triangle,
the ratio of hypotenuse to leg length is   ,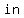
so I need not think much to know for triangle ADC the hypotenuse length is
 .
Alternative ways to get to the solution:
Knowing that ADC is an isosceles right triangle,
we could apply the Pythagorean theorem
to calculate the length hypotenuse AC, in inches, as
Otherwise, knowing that ADC is a right triangle with
m∠ACD = 45° ,
we can calculate the trigonometric ratio for angle ACD
cos(ACD)=(adjacent side)/hypotenuse
and substituting known values,
Dividing vt both sides of the equal sign,
 ,
and multiplying both sides times 
 .
NOTE:
BY the way, all those triangles are isosceles right triangles,
DCB is congruent with ACD, and ABC is similar, to DCB and DCA,
larger by a scale factor od , of course.
|
|
|
