Question 626330: Suppose that A, B, and C are positive constants and that x+y= C. Show that the minimum value of 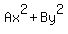 occurs when occurs when  and and 
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Suppose that A, B, and C are positive constants and that x + y = C. Show that the minimum value of Ax² + By² occurs when x =  and y = and y = 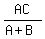
We know that if A > 0, the minimum value of y = Ax² + Bx + C
occurs when x = 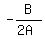 To avoid conflict of letters we re-write that as
We know that if P > 0, the minimum value of y = Px² + Qx + R
occurs when x =
To avoid conflict of letters we re-write that as
We know that if P > 0, the minimum value of y = Px² + Qx + R
occurs when x = 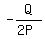 Since x + y = C, y = C - x, so
Minimum value of Ax² + By² =
Minimum value of Ax² + B(C - x)² =
Minimum value of Ax² + B(C - x)(C - x) =
Minimum value of Ax² + B(C² - 2Cx + x²) =
Minimum value of Ax² + BC² - 2BCx + Bx² =
Minimum value of Ax² + Bx² - 2BCx + BC² =
Minimum value of (A + B)x² - 2BCx + BC²
And by the rule above:
We know that if P > 0, the minimum value of y = Px² + Qx + R
occurs when x =
Since x + y = C, y = C - x, so
Minimum value of Ax² + By² =
Minimum value of Ax² + B(C - x)² =
Minimum value of Ax² + B(C - x)(C - x) =
Minimum value of Ax² + B(C² - 2Cx + x²) =
Minimum value of Ax² + BC² - 2BCx + Bx² =
Minimum value of Ax² + Bx² - 2BCx + BC² =
Minimum value of (A + B)x² - 2BCx + BC²
And by the rule above:
We know that if P > 0, the minimum value of y = Px² + Qx + R
occurs when x = 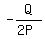 Let P = (A + B), Q = -2BC, and R = BC²
Minimum value of (A + B)x² - 2BCx + BC²
occurs when x =
Let P = (A + B), Q = -2BC, and R = BC²
Minimum value of (A + B)x² - 2BCx + BC²
occurs when x = 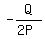 = = 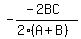 = =  and since y = C - x, the value of y when x =
and since y = C - x, the value of y when x =  is
y = C - is
y = C -  = =  - -  = =
 · ·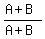 - -  = =  - -  = =
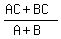 - -  = = 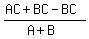 = =  .
Edwin .
Edwin
|
|
|