.
Find the number of ordered pairs (a,b) of integers such that
 =
=  .
.
~~~~~~~~~~~~~~~~~~~~~~~~~~
From  =
=  we have
we have
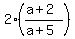 = b,
= b,
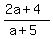 = b,
2 -
= b,
2 - 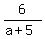 = b,
so if "b" is an integer number, then
= b,
so if "b" is an integer number, then 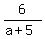 must be integer.
It means that a+5 must divide 6 with zero remainder.
Hence, possible values for a+5 are
a+5 = 6, a+5 = 3, a+5 = 2, a+5 = 1, a+5 = -1, a+5 = -2, a+5 = -3, a+5 = -6.
Thus we have 8 different integer values for "a" that satisfy the condition,
and, obviously, they produce 8 different ordered pairs of integer numbers (a,b).
So, the ANSWER to the problem's question is: there are 8 different pairs (a,b) of integer number such that
must be integer.
It means that a+5 must divide 6 with zero remainder.
Hence, possible values for a+5 are
a+5 = 6, a+5 = 3, a+5 = 2, a+5 = 1, a+5 = -1, a+5 = -2, a+5 = -3, a+5 = -6.
Thus we have 8 different integer values for "a" that satisfy the condition,
and, obviously, they produce 8 different ordered pairs of integer numbers (a,b).
So, the ANSWER to the problem's question is: there are 8 different pairs (a,b) of integer number such that  =
=  .
.
Solved.