Question 1171717: What is the maximum value of k, if the solutions for the two equations below are the same, and both x and y are integers?
(x+5)² + (y-1)² = 25
-2x + 3y = k
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Put the second in slope-intercept form:
Put the second in slope-intercept form:


 The first equation is a circle and the second represents a set of parallel lines with slope 2/3 and y-intercept k/3.
The first equation is a circle and the second represents a set of parallel lines with slope 2/3 and y-intercept k/3.
 We want to find the maximum value of k. k will be a maximum when k/3 is
a maximum. k/3 is the y-intercept and it will be a maximum when the y-intercept
is the largest. That will be when the line is the upper tangent to the circle.
Like this:
We want to find the maximum value of k. k will be a maximum when k/3 is
a maximum. k/3 is the y-intercept and it will be a maximum when the y-intercept
is the largest. That will be when the line is the upper tangent to the circle.
Like this:
 We know the distance from the center (-5,1) to the point of tangency is the
radius, which is 5. So we use the formula for the perpendicular distance
from a point to a line, which is
The perpendicular distance from the point (x1,y1) to the line Ax + By + C = 0
is given by the formula:
We know the distance from the center (-5,1) to the point of tangency is the
radius, which is 5. So we use the formula for the perpendicular distance
from a point to a line, which is
The perpendicular distance from the point (x1,y1) to the line Ax + By + C = 0
is given by the formula:
 So the perpendicular distance from the center (-5,1) to the line
-2x + 3y - k = 0 is equal to the radius 5, so
So the perpendicular distance from the center (-5,1) to the line
-2x + 3y - k = 0 is equal to the radius 5, so




 or or 
 or or 
 The first is the lower tangent line, so we
want the upper tangent line,
So the maximum value of k is
The first is the lower tangent line, so we
want the upper tangent line,
So the maximum value of k is
 which is approximately 31.02775638
The largest potential integer k is 31.
And it does turn out that when k=31 which is approximately 31.02775638
The largest potential integer k is 31.
And it does turn out that when k=31
 We get two solutions (x,y) = (-8,5) and (x,y) =
We get two solutions (x,y) = (-8,5) and (x,y) = 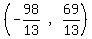 So x=-8, y=5, is an integer solution that allows k to be the maximum integer
value of 31.
Edwin
So x=-8, y=5, is an integer solution that allows k to be the maximum integer
value of 31.
Edwin
|
|
|