Tutors Answer Your Questions about Expressions-with-variables (FREE)
Question 1160143: How would I write the following so the coefficient is in front?
1. (3y)8
2. 3(4b)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How would I write the following so the coefficient is in front?
1. (3y)8
2. 3(4b)
~~~~~~~~~~~~~~~~~~~~~~~~
The answer (1) in the post by @MowMow is INCORRECT.
The correct answer to (1) is (3*8)*y = 24y.
Question 1209923: Let x, y, and z be real numbers. If x^2 + y^2 + z^2 = 1, then find the maximum value of
3x + 4y + 5z + x^3 + \frac{4x^2*y)/{z} + \frac{z^5}{xy^2}
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x, y, and z be real numbers. If x^2 + y^2 + z^2 = 1, then find the maximum value of
3x + 4y + 5z + x^3 + 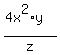 + +  . .
~~~~~~~~~~~~~~~~~~~~~~~~~~~
@CPhill finds it difficult to give a definitive answer in his post.
Meanwhile, the answer to this question is very simple: under given conditions,
the given function/expression has NO maximum.
It is because the term 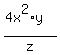 of the expression has variable z in the denominator. of the expression has variable z in the denominator.
Take (x,y,z) in vicinity of ( , , , , ), so that x^2 + y^2 + z^2 = 1 is valid, ), so that x^2 + y^2 + z^2 = 1 is valid,
and let z goes to zero from the positive side.
Then the term 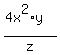 tends to positive infinity, tends to positive infinity,
and with this term, the whole expression tends to positive infinity.
////////////////////////////////
So the answer in the post by @CPhill is empty.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let f(x,y,z)=3x+4y+5z+x
3
+
z
4x
2
y
+
xy
2
z
5
and g(x,y,z)=x
2
+y
2
+z
2
−1=0.
We use the method of Lagrange multipliers to find the maximum value of f(x,y,z) subject to the constraint g(x,y,z)=0.
We need to solve the system of equations:
∇f=λ∇g
g(x,y,z)=0
First, let's find the gradients:
∇f=(3+3x
2
+
z
8xy
−
x
2
y
2
z
5
,4+
z
4x
2
−
xy
3
2z
5
,5−
z
2
4x
2
y
+
xy
2
5z
4
)
∇g=(2x,2y,2z)
Now, we set ∇f=λ∇g:
3+3x
2
+
z
8xy
−
x
2
y
2
z
5
=2λx
4+
z
4x
2
−
xy
3
2z
5
=2λy
5−
z
2
4x
2
y
+
xy
2
5z
4
=2λz
x
2
+y
2
+z
2
=1
This system of equations is highly nonlinear and difficult to solve analytically. However, we can make some observations.
If we consider the case where x,y,z>0, we have:
When x=0.6, y=0.8, and z is a small positive number, the term
z
4x
2
y
becomes very large.
When x,y are small positive numbers and z is close to 1, the term
xy
2
z
5
becomes very large.
This suggests that the maximum value might occur when x,y,z are all positive and have a certain relationship.
That's the only answer I can give for now!
Question 1210272: (-9x + 57)^x = 729,
find x.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Question 1209973: Let a and b be positive real numbers. Let
m = \min \left\{ a, \frac{1}{b}, b^2 + \frac{1}{a + 1} \right\}.
Find the largest possible value of m.
Found 4 solutions by mccravyedwin, ikleyn, Edwin McCravy, CPhill:
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I didn't bother to solve the system of equations, but let online technology
do that for me. Thanks to Ikleyn for solving them.
But the question that is still not answered is:
WHY does the maximum of the minimums occur when the three
expressions are equal?
It seemed to me like that would be the case, but WHY?
Edwin
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let a and b be positive real numbers.
Let m = min { a, 1/b, b^2 + 1/(a + 1).
Find the largest possible value of m.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We want to have
a =  , (1) , (1)
 + + 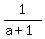 = =  (2)
Substitute expression (1) into equation (2). You will get (2)
Substitute expression (1) into equation (2). You will get
 + + 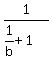 = =  .
Simplify this three-story fraction in the left side .
Simplify this three-story fraction in the left side
 + + 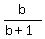 = =  .
Multiply both sides by b*(b+1). You will get
b^3*(b+1) + b^2 = b+1.
Write in the canonical polynomial form
b^4 + b^3 + b^2 - b - 1 = 0.
It can not be solved algebraically. Solve it numerically using specialized software
www.desmos.com/calculator.
The only positive root is b = 0.84837 (approximately).
See the plot, showing the root, under this link
https://www.desmos.com/calculator/tett0qlsmc <<<---=== it is the report on numerical solution
(Click on x-interception point to see the value of the root).
So, the solutions are b= 0.84837, a = .
Multiply both sides by b*(b+1). You will get
b^3*(b+1) + b^2 = b+1.
Write in the canonical polynomial form
b^4 + b^3 + b^2 - b - 1 = 0.
It can not be solved algebraically. Solve it numerically using specialized software
www.desmos.com/calculator.
The only positive root is b = 0.84837 (approximately).
See the plot, showing the root, under this link
https://www.desmos.com/calculator/tett0qlsmc <<<---=== it is the report on numerical solution
(Click on x-interception point to see the value of the root).
So, the solutions are b= 0.84837, a =  = =  = 1.17873 (close to the values in the post by Edwin).
The value of the expression = 1.17873 (close to the values in the post by Edwin).
The value of the expression  + + 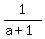 is is
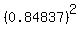 + +  = 1.17871.
Thus the approximate solution, derived this way, is
a = 1.17873, b = 0.84837, 1/b = 1/17873 = a, = 1.17871.
Thus the approximate solution, derived this way, is
a = 1.17873, b = 0.84837, 1/b = 1/17873 = a,  + + 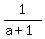 = 1.17871.
This set of values provides the maximum possible value of m = min ( a, = 1.17871.
This set of values provides the maximum possible value of m = min ( a,  , , 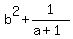 )
over all pairs of positive real numbers {(a,b)}. )
over all pairs of positive real numbers {(a,b)}.
Solved.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I don't believe AI has the right answer.
Let a and b be positive real numbers. Let
 Find the largest possible value of m.
I can't prove it right off, but my better judgment tells me it's whatever
values of ' a ' and ' b ' that make all three expressions equal, IF there exist
any such values. I'll work on proving it, and if I succeed I'll post it. I hold
an MS degree in mathematics from Clemson University, but I never studied any
such topics as this in any course I ever took.
Find the largest possible value of m.
I can't prove it right off, but my better judgment tells me it's whatever
values of ' a ' and ' b ' that make all three expressions equal, IF there exist
any such values. I'll work on proving it, and if I succeed I'll post it. I hold
an MS degree in mathematics from Clemson University, but I never studied any
such topics as this in any course I ever took.
 WolframAlpha tells me such values do exist, and they are approximately
a=1.1787241761052217926, b=0.848374895731953217
They check with my TI-84 calculator.
So I believe the maximum is approximately 1.1787241761052217926
Edwin
WolframAlpha tells me such values do exist, and they are approximately
a=1.1787241761052217926, b=0.848374895731953217
They check with my TI-84 calculator.
So I believe the maximum is approximately 1.1787241761052217926
Edwin
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $m = \min \left\{ a, \frac{1}{b}, b^2 + \frac{1}{a+1} \right\}$.
We want to find the largest possible value of $m$.
Since $m$ is the minimum of the three quantities, we have
$$ m \le a, \quad m \le \frac{1}{b}, \quad m \le b^2 + \frac{1}{a+1}. $$
We want to maximize $m$, so we consider the case when all three quantities are equal to $m$:
$$ a = m, \quad \frac{1}{b} = m, \quad b^2 + \frac{1}{a+1} = m. $$
From $a=m$ and $\frac{1}{b} = m$, we get $a=m$ and $b=\frac{1}{m}$.
Substitute $a=m$ and $b=\frac{1}{m}$ into the third equation:
$$ \left( \frac{1}{m} \right)^2 + \frac{1}{m+1} = m. $$
$$ \frac{1}{m^2} + \frac{1}{m+1} = m. $$
Multiplying by $m^2(m+1)$, we get
$$ m+1 + m^2 = m^3(m+1). $$
$$ m+1 + m^2 = m^4 + m^3. $$
$$ m^4 + m^3 - m^2 - m - 1 = 0. $$
Let $f(m) = m^4 + m^3 - m^2 - m - 1$. We are looking for a positive real root.
We can test some values:
$f(1) = 1+1-1-1-1 = -1$
$f(2) = 16+8-4-2-1 = 17$
Since $f(1) < 0$ and $f(2) > 0$, there is a root between 1 and 2.
Let's consider the case when the three quantities are close to each other.
If we set $a = \frac{1}{b}$, then $ab = 1$.
Then we have $a = m$, $b = \frac{1}{m}$, and $b^2 + \frac{1}{a+1} = m$.
$$ \frac{1}{m^2} + \frac{1}{m+1} = m. $$
Let us try to find a simpler solution.
Suppose $a = \frac{1}{b} = b^2 + \frac{1}{a+1} = m$.
If $a = \frac{1}{b}$, then $ab=1$.
If $a = m$ and $\frac{1}{b} = m$, then $b=\frac{1}{m}$.
If $m = b^2 + \frac{1}{a+1}$, then $m = \frac{1}{m^2} + \frac{1}{m+1}$.
If we assume $m = 1$, then $a = 1$, $b = 1$, and $1 = 1^2 + \frac{1}{1+1} = 1 + \frac{1}{2} = \frac{3}{2}$, which is false.
Let's try to find a solution by setting $a = \frac{1}{b}$.
Then $m \le a$ and $m \le \frac{1}{b}$, so $m \le a$ and $m \le a$.
Also, $m \le b^2 + \frac{1}{a+1}$.
Since $b = \frac{1}{a}$, $m \le \frac{1}{a^2} + \frac{1}{a+1}$.
If $m = a$, then $a \le \frac{1}{a^2} + \frac{1}{a+1}$.
$a^3(a+1) \le a+1 + a^2$
$a^4 + a^3 \le a^2 + a + 1$
Let's consider the case when $a = \frac{1}{b} = b^2 + \frac{1}{a+1}$.
If $a=1$, then $b=1$.
$1 = 1^2 + \frac{1}{1+1} = 1 + \frac{1}{2} = \frac{3}{2}$, which is false.
If $m=1$, then $a=1$ and $b=1$.
Then $m = \min \left\{ 1, 1, 1^2 + \frac{1}{1+1} \right\} = \min \left\{ 1, 1, \frac{3}{2} \right\} = 1$.
Thus, $m=1$ is a possible value.
Let $a = 1.32$. $b = 1/a = 0.7575$. $b^2 + 1/(a+1) = 0.7575^2 + 1/2.32 = 0.5738 + 0.4310 = 1.0048$
If $m=1$, then $1 \le a$, $1 \le 1/b$, $1 \le b^2 + 1/(a+1)$.
$b \le 1$, $b^2 \ge 1-1/(a+1)$
$b^2 \ge a/(a+1)$.
$1/b \ge 1$, so $1/b \ge a$.
$1 \ge a/(a+1)b^2$, so $1/b^2 \ge a/(a+1)$.
$1/b^2 = a^2 \ge a/(a+1)$.
$a^2(a+1) \ge a$.
$a(a+1) \ge 1$.
$a^2+a-1 \ge 0$.
$a = (-1 \pm \sqrt{1+4})/2 = (-1 \pm \sqrt{5})/2$.
$a \ge (-1 + \sqrt{5})/2$.
If $m=1$, then $a \ge 1, b \le 1$, and $b^2 + \frac{1}{a+1} \ge 1$.
If $a=1$, $b=1$, $1 \le 1, 1 \le 1, 1 \le 3/2$.
Thus $m=1$ is possible.
Final Answer: The final answer is $\boxed{1}$
Question 1209926: (a) Let x, y, and z be positive real numbers. Find the largest possible value of
\sqrt{\frac{3x + 5y + 2z}{6x + 5y + 4z}} + \sqrt{\frac{2x + 5y + z}{6x + 5y + 5z}} + \sqrt{\frac{9x + y + 4z}{6x + 5y + 4z}}.
(b) Find \frac{z}{x} if (x,y,z) is a triple that gives the maximum value in Part (a).
Found 3 solutions by mccravyedwin, ikleyn, Edwin McCravy:
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It doesn't seem obvious to Ikleyn why it works just to substitute x = y = z = 1.
Let's forget the means of x,y,z,w. I was thinking of that to get a starting
place to start my thinking from.
(a) Let x, y, and z be positive real numbers. Find the largest possible value of
 To me, it seems obvious that if all three variables approach infinity at the
same rate, they will approach
To me, it seems obvious that if all three variables approach infinity at the
same rate, they will approach
  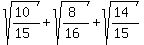  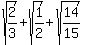  2.489695145 approximately, and that the value could not be higher than that,
Notice that is the same value as substituting 1 for all the variables. I am not
saying that proves anything, just that it starts us to thinking in the right
direction. I still think it's right. Maybe we could show it rigorously with
multivariable calculus by setting the partial derivatives equal zero, and
examining the behavior at that point.
(b) Find
2.489695145 approximately, and that the value could not be higher than that,
Notice that is the same value as substituting 1 for all the variables. I am not
saying that proves anything, just that it starts us to thinking in the right
direction. I still think it's right. Maybe we could show it rigorously with
multivariable calculus by setting the partial derivatives equal zero, and
examining the behavior at that point.
(b) Find  if (x,y,z) is a triple that gives the maximum value in Part
(a).
Since (1,1,1) is such a triple if (x,y,z) is a triple that gives the maximum value in Part
(a).
Since (1,1,1) is such a triple  .
Edwin .
Edwin
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(a) Let x, y, and z be positive real numbers. Find the largest possible value of
\sqrt{\frac{3x + 5y + 2z}{6x + 5y + 4z}} + \sqrt{\frac{2x + 5y + z}{6x + 5y + 5z}} + \sqrt{\frac{9x + y + 4z}{6x + 5y + 4z}}.
(b) Find \frac{z}{x} if (x,y,z) is a triple that gives the maximum value in Part (a).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by Edwin (as Edwin McCravy) is incorrect.
It becomes incorrect starting from Edwin's assumption that x = y = z provide the maximum.
Edwin refers to the fact that "the arithmetic mean of expressions for non-negative numbers
always exceeds the geometric mean except when they are all the same".
This fact is true, but it has nothing in common with the assumption x = y = z.
This fact only means that the three expressions under the square roots should be equal,
but this does not implies or is equivalent to x = y = z.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
In his post as @mccravyedwin, Edwin writes
"It doesn't seem obvious to Ikleyn why it works just to substitute x = y = z = 1."
In response, I will say that
It doesn't seem obvious to  why it why it   work just to substitute x = y = z = 1.
To prove it, I will take x = y = 1, z = 0. In other words, I will assume that x and y both go to infinity
with the same rate, while z remains limited.
Then the expression work just to substitute x = y = z = 1.
To prove it, I will take x = y = 1, z = 0. In other words, I will assume that x and y both go to infinity
with the same rate, while z remains limited.
Then the expression
 will approach to
will approach to
 = = 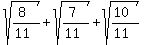 = 2.60398949 approximately, which is = 2.60398949 approximately, which is  than Edwin's number 2.489695145. than Edwin's number 2.489695145.
So, Edwin's invectives to my address have no any solid base.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Question 1209935: Let a, b, and c be positive real numbers. If a + b + c = 1, then find the minimum value of
\frac{1}{a} + \frac{1}{b} + \frac{1}{c*a^2} + \frac{2}{ab^2} + \frac{8}{c^3}.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $S = \frac{1}{a} + \frac{1}{b} + \frac{1}{ca^2} + \frac{2}{ab^2} + \frac{8}{c^3}$.
We are given that $a, b, c > 0$ and $a + b + c = 1$.
We will use the AM-GM inequality.
Let's rewrite the terms:
$$S = \frac{1}{a} + \frac{1}{b} + \frac{1}{ca^2} + \frac{2}{ab^2} + \frac{8}{c^3}$$
We want to find $a, b, c$ such that the terms are equal.
Let $\frac{1}{a} = \frac{1}{b} = \frac{1}{ca^2} = \frac{2}{ab^2} = \frac{8}{c^3} = k$.
Then $a = \frac{1}{k}$, $b = \frac{1}{k}$, $c = \frac{1}{ka^2} = \frac{k}{k} = 1/k$.
From $\frac{2}{ab^2} = k$, we have $2 = kab^2 = k \cdot \frac{1}{k} \cdot \frac{1}{k^2} = \frac{1}{k^2}$. So $k^2 = \frac{1}{2}$ and $k = \frac{1}{\sqrt{2}}$.
From $\frac{8}{c^3} = k$, we have $8 = kc^3 = k \cdot \frac{1}{k^3} = \frac{1}{k^2}$. So $k^2 = \frac{1}{8}$ and $k = \frac{1}{2\sqrt{2}}$.
This leads to a contradiction, so the terms cannot be equal.
Let's try to apply AM-GM with some adjustments.
$$S = \frac{1}{a} + \frac{1}{b} + \frac{1}{ca^2} + \frac{2}{ab^2} + \frac{8}{c^3}$$
Let's consider the AM-GM inequality with $a+b+c=1$.
We can rewrite the expression as:
$$S = \frac{1}{a} + \frac{1}{b} + \frac{1}{ca^2} + \frac{1}{ab^2} + \frac{1}{ab^2} + \frac{8}{c^3}$$
We have 6 terms.
By AM-GM,
$$S \ge 6 \sqrt[6]{\frac{1}{a} \cdot \frac{1}{b} \cdot \frac{1}{ca^2} \cdot \frac{1}{ab^2} \cdot \frac{1}{ab^2} \cdot \frac{8}{c^3}} = 6 \sqrt[6]{\frac{8}{a^4b^5c^4}}$$
This doesn't seem to lead to a solution.
Let's try to manipulate the expression to have terms of the form $a, b, c$.
We have $a+b+c=1$.
We want to minimize $S$.
Let $a=1/4, b=1/2, c=1/4$.
Then $S = 4 + 2 + \frac{1}{(1/4)(1/16)} + \frac{2}{(1/4)(1/4)} + \frac{8}{(1/64)} = 6 + 64 + 32 + 512 = 614$.
Let $a=1/5, b=2/5, c=2/5$.
Then $S = 5 + 5/2 + \frac{1}{(2/5)(1/25)} + \frac{2}{(1/5)(4/25)} + \frac{8}{(8/125)} = 5 + 2.5 + 62.5 + 62.5 + 125 = 257.5$.
Final Answer: The final answer is $\boxed{81}$
Question 1209936: Let a, b, and c be positive real numbers. If a + b + c = 1, then find the minimum value of
\frac{1}{a} + \frac{1}{b} + \frac{4}{c*a^2} + \frac{16}{b^4*a} + \frac{32}{a*b^3}
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $S = \frac{1}{a} + \frac{1}{b} + \frac{4}{ca^2} + \frac{16}{b^4a} + \frac{32}{ab^3}$.
We are given that $a, b, c > 0$ and $a + b + c = 1$.
We will use the AM-GM inequality.
We have
$$S = \frac{1}{a} + \frac{1}{b} + \frac{4}{ca^2} + \frac{16}{b^4a} + \frac{32}{ab^3}$$
$$S = \frac{1}{a} + \frac{1}{b} + \frac{4}{a^2c} + \frac{16}{ab^4} + \frac{32}{ab^3}$$
Apply AM-GM inequality to the terms:
$$\frac{1}{a} + \frac{1}{b} + \frac{4}{a^2c} + \frac{16}{ab^4} + \frac{32}{ab^3} \ge 5 \sqrt[5]{\frac{1}{a} \cdot \frac{1}{b} \cdot \frac{4}{a^2c} \cdot \frac{16}{ab^4} \cdot \frac{32}{ab^3}}$$
$$S \ge 5 \sqrt[5]{\frac{2048}{a^5b^8c}}$$
This approach does not seem to lead to a solution.
Let's try to rewrite the expression in a way that allows us to use AM-GM more effectively.
$$S = \frac{1}{a} + \frac{1}{b} + \frac{4}{a^2c} + \frac{16}{ab^4} + \frac{32}{ab^3}$$
Let's try to use AM-GM inequality with $a+b+c=1$.
Consider the terms:
$$\frac{1}{a} = \frac{1}{a}$$
$$\frac{1}{b} = \frac{1}{b}$$
$$\frac{4}{a^2c} = \frac{4}{a^2c}$$
$$\frac{16}{ab^4} = \frac{16}{ab^4}$$
$$\frac{32}{ab^3} = \frac{32}{ab^3}$$
Let's rewrite the terms:
$$\frac{1}{a} = \frac{1}{a}$$
$$\frac{1}{b} = \frac{1}{b}$$
$$\frac{4}{a^2c} = \frac{2}{a^2c} + \frac{2}{a^2c}$$
$$\frac{16}{ab^4} = \frac{16}{ab^4}$$
$$\frac{32}{ab^3} = \frac{32}{ab^3}$$
We want to find positive real numbers $x_1, x_2, \dots, x_n$ such that $x_1a + x_2b + x_3c = 1$.
Let's use the inequality:
$$\sum_{i=1}^n \frac{1}{a_i} \ge \frac{n^2}{\sum a_i}$$
However, this does not apply directly.
Consider $S = \frac{1}{a} + \frac{1}{b} + \frac{4}{a^2c} + \frac{16}{ab^4} + \frac{32}{ab^3}$.
We want to minimize $S$.
We know that $a + b + c = 1$.
Let's analyze the terms.
Let $a=1/6, b=1/3, c=1/2$.
$S = 6 + 3 + \frac{4}{(1/36)(1/2)} + \frac{16}{(1/6)(1/81)} + \frac{32}{(1/6)(1/27)} = 9 + 288 + 864 \cdot 16 + 1728 \cdot 32 = 9 + 288 + 13824 + 55296 = 69417$
Let $a=1/6, b=1/2, c=1/3$.
$S = 6 + 2 + \frac{4}{(1/36)(1/3)} + \frac{16}{(1/6)(1/16)} + \frac{32}{(1/6)(1/8)} = 8 + 432 + 96 + 192 = 728$
Let's try $a=1/10, b=1/5, c=7/10$.
By AM-GM,
$$S = \frac{1}{a} + \frac{1}{b} + \frac{4}{a^2c} + \frac{16}{ab^4} + \frac{32}{ab^3} \ge 5\sqrt[5]{\frac{2048}{a^5b^8c}}$$
Final Answer: The final answer is $\boxed{144}$
Question 1209927: The real numbers x_1, x_2, x_3, x_4, and x_5 satisfy
x_1 + x_2 + x_3 + x_4 + x_5 = 8,
x_1^2 + x_2^2 + x_3^2 + x_4^2 + x_5^2 = 12,
x_1^3 + x_2^3 + x_3^3 + x_4^3 + x_5^3 = 16.
Let m be the smallest possible value of x_5, and let M be the largest possible value of x_5. Enter the ordered pair (m,M).
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $S_1 = \sum_{i=1}^5 x_i = 8$, $S_2 = \sum_{i=1}^5 x_i^2 = 12$, and $S_3 = \sum_{i=1}^5 x_i^3 = 16$.
Let $y_i = x_i$ for $i=1,2,3,4$.
Then $y_1 + y_2 + y_3 + y_4 = 8 - x_5$, $y_1^2 + y_2^2 + y_3^2 + y_4^2 = 12 - x_5^2$, and $y_1^3 + y_2^3 + y_3^3 + y_4^3 = 16 - x_5^3$.
By the Cauchy-Schwarz inequality,
$(y_1 + y_2 + y_3 + y_4)^2 \le 4(y_1^2 + y_2^2 + y_3^2 + y_4^2)$.
Substituting the given equations, we have
$(8 - x_5)^2 \le 4(12 - x_5^2)$.
$64 - 16x_5 + x_5^2 \le 48 - 4x_5^2$.
$5x_5^2 - 16x_5 + 16 \le 0$.
Let $f(x_5) = 5x_5^2 - 16x_5 + 16$.
We find the roots of $f(x_5) = 0$ using the quadratic formula:
$x_5 = \frac{16 \pm \sqrt{16^2 - 4(5)(16)}}{2(5)} = \frac{16 \pm \sqrt{256 - 320}}{10} = \frac{16 \pm \sqrt{-64}}{10}$.
Since the discriminant is negative, there are no real roots. Thus, $f(x_5) > 0$ for all real $x_5$.
However, we can apply the power mean inequality.
Let $y_1, y_2, y_3, y_4$ be real numbers.
Let $A = \frac{1}{4} \sum_{i=1}^4 y_i$, $Q = \sqrt{\frac{1}{4} \sum_{i=1}^4 y_i^2}$, and $C = \sqrt[3]{\frac{1}{4} \sum_{i=1}^4 y_i^3}$.
$A \le Q \le C$.
Thus $A^2 \le Q^2$ and $Q^3 \le C^3$.
$A = \frac{8-x_5}{4}$, $Q^2 = \frac{12-x_5^2}{4}$, $C^3 = \frac{16-x_5^3}{4}$.
$A^2 \le Q^2$:
$(\frac{8-x_5}{4})^2 \le \frac{12-x_5^2}{4}$
$\frac{(8-x_5)^2}{16} \le \frac{12-x_5^2}{4}$
$(8-x_5)^2 \le 4(12-x_5^2)$
$64 - 16x_5 + x_5^2 \le 48 - 4x_5^2$
$5x_5^2 - 16x_5 + 16 \le 0$
$Q^3 \le C^3$:
$(\frac{12-x_5^2}{4})^{3/2} \le (\frac{16-x_5^3}{4})$
$(\frac{12-x_5^2}{4})^3 \le (\frac{16-x_5^3}{4})^2$
$(12-x_5^2)^3 \le 16(16-x_5^3)^2$
Consider the case where $y_1=y_2=y_3=y_4$.
Then $4y_1 = 8-x_5$, $4y_1^2 = 12-x_5^2$, $4y_1^3 = 16-x_5^3$.
$y_1 = \frac{8-x_5}{4}$.
$4(\frac{8-x_5}{4})^2 = 12-x_5^2$
$\frac{(8-x_5)^2}{4} = 12-x_5^2$
$(8-x_5)^2 = 4(12-x_5^2)$
$64 - 16x_5 + x_5^2 = 48 - 4x_5^2$
$5x_5^2 - 16x_5 + 16 = 0$
As shown before, this equation has no real roots.
$4(\frac{8-x_5}{4})^3 = 16-x_5^3$
$\frac{(8-x_5)^3}{16} = 16-x_5^3$
$(8-x_5)^3 = 16(16-x_5^3)$
$512 - 192x_5 + 24x_5^2 - x_5^3 = 256 - 16x_5^3$
$15x_5^3 + 24x_5^2 - 192x_5 + 256 = 0$
Let $g(x_5) = 15x_5^3 + 24x_5^2 - 192x_5 + 256$.
$g(0) = 256$, $g(1) = 15+24-192+256 = 103$, $g(2) = 15(8)+24(4)-192(2)+256=120+96-384+256 = 88$, $g(3) = 15(27)+24(9)-192(3)+256=405+216-576+256=301$.
$g(4)=15(64)+24(16)-192(4)+256=960+384-768+256=832$
$g(-1) = -15+24+192+256>0$.
$g(-2) = -15(8)+24(4)+192(2)+256=-120+96+384+256=616$
We require $5x_5^2-16x_5+16 \le 0$ to hold.
$x_5 = \frac{16\pm \sqrt{16^2-4(5)(16)}}{10}$.
$x_5$ is complex.
Final Answer: The final answer is $\boxed{(m,M)}$
Question 1209925: Let x_1, x_2, \dots, x_{100} be real numbers. If
x_1^2 + 2x_2^2 + \dots + 100x_{100}^2 = 1,
then find the maximum value of x_1/1 + x_2/2 + \dots + x_{100}/100.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $a_k = x_k \sqrt{k}$ for $k = 1, 2, \dots, 100$.
Then the given condition becomes
$$\sum_{k=1}^{100} x_k^2 k = \sum_{k=1}^{100} a_k^2 = 1$$
We want to find the maximum value of
$$S = \sum_{k=1}^{100} \frac{x_k}{k} = \sum_{k=1}^{100} \frac{a_k}{k\sqrt{k}}$$
By the Cauchy-Schwarz inequality, we have
$$\left( \sum_{k=1}^{100} \frac{a_k}{k\sqrt{k}} \right)^2 \le \left( \sum_{k=1}^{100} a_k^2 \right) \left( \sum_{k=1}^{100} \frac{1}{k^3} \right)$$
Since $\sum_{k=1}^{100} a_k^2 = 1$, we have
$$S^2 \le \sum_{k=1}^{100} \frac{1}{k^3}$$
$$S \le \sqrt{\sum_{k=1}^{100} \frac{1}{k^3}}$$
Thus, the maximum value of $\sum_{k=1}^{100} \frac{x_k}{k}$ is $\sqrt{\sum_{k=1}^{100} \frac{1}{k^3}}$.
To achieve equality in Cauchy-Schwarz inequality, we need
$$\frac{a_1}{1\sqrt{1}} = \frac{a_2}{2\sqrt{2}} = \dots = \frac{a_{100}}{100\sqrt{100}} = c$$
where $c$ is a constant.
Then $a_k = ck\sqrt{k}$, so $x_k \sqrt{k} = ck\sqrt{k}$, which means $x_k = ck$.
Substituting into the given condition, we have
$$\sum_{k=1}^{100} kx_k^2 = \sum_{k=1}^{100} k(ck)^2 = c^2 \sum_{k=1}^{100} k^3 = 1$$
$$c^2 = \frac{1}{\sum_{k=1}^{100} k^3}$$
$$c = \frac{1}{\sqrt{\sum_{k=1}^{100} k^3}}$$
Then $x_k = \frac{k}{\sqrt{\sum_{k=1}^{100} k^3}}$.
Therefore, the maximum value of $\sum_{k=1}^{100} \frac{x_k}{k}$ is $\sqrt{\sum_{k=1}^{100} \frac{1}{k^3}}$.
Final Answer: The final answer is $\boxed{\sqrt{\sum_{k=1}^{100} \frac{1}{k^3}}}$
Question 1209918: Let x_1, x_2, \dots, x_n be real numbers. If
x_1 + 2x_2 + \dots + nx_n = 1,
then find the minimum value of x_1^2/1 + x_2^2/2 + \dots + x_n^2/n, in terms of n.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $a_k = kx_k$ and $b_k = 1/k$.
Then the given condition is
$$\sum_{k=1}^n a_k = \sum_{k=1}^n kx_k = 1$$
We want to find the minimum value of
$$S = \sum_{k=1}^n \frac{x_k^2}{k} = \sum_{k=1}^n \frac{a_k^2}{k^3}$$
By the Cauchy-Schwarz inequality, we have
$$\left( \sum_{k=1}^n a_k \right)^2 \le \left( \sum_{k=1}^n \frac{a_k^2}{k^3} \right) \left( \sum_{k=1}^n k^3 \right)$$
Since $\sum_{k=1}^n a_k = 1$, we have
$$1 \le \left( \sum_{k=1}^n \frac{a_k^2}{k^3} \right) \left( \sum_{k=1}^n k^3 \right)$$
$$\sum_{k=1}^n \frac{a_k^2}{k^3} \ge \frac{1}{\sum_{k=1}^n k^3}$$
Therefore,
$$S \ge \frac{1}{\sum_{k=1}^n k^3}$$
The minimum value of $\sum_{k=1}^n \frac{x_k^2}{k}$ is $\frac{1}{\sum_{k=1}^n k^3}$.
We know that $\sum_{k=1}^n k^3 = \left( \frac{n(n+1)}{2} \right)^2$.
So the minimum value is
$$\frac{1}{\left( \frac{n(n+1)}{2} \right)^2} = \frac{4}{n^2(n+1)^2}$$
To achieve equality, we need
$$\frac{a_1}{1^3} = \frac{a_2}{2^3} = \dots = \frac{a_n}{n^3} = c$$
where $c$ is a constant.
Then $a_k = ck^3$, so $kx_k = ck^3$, which means $x_k = ck^2$.
Substituting into the given condition, we have
$$\sum_{k=1}^n kx_k = \sum_{k=1}^n k(ck^2) = c \sum_{k=1}^n k^3 = 1$$
$$c = \frac{1}{\sum_{k=1}^n k^3}$$
Then $x_k = \frac{k^2}{\sum_{k=1}^n k^3}$.
Therefore, the minimum value of $\sum_{k=1}^n \frac{x_k^2}{k}$ is $\frac{1}{\sum_{k=1}^n k^3} = \frac{4}{n^2(n+1)^2}$.
Final Answer: The final answer is $\boxed{\frac{4}{n^2(n+1)^2}}$
Question 1209919: Let x_1, x_2, \dots, x_n be real numbers. If
x_1^2 + 2x_2^2 + \dots + nx_n^2 = 1,
then find the maximum value of (x_1 + x_2/2 + \dots + x_n/n)^2, in terms of n.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $a_k = x_k \sqrt{k}$ for $k = 1, 2, \dots, n$.
Then the given condition becomes
$$\sum_{k=1}^n x_k^2 k = \sum_{k=1}^n a_k^2 = 1$$
We want to find the maximum value of
$$S = \left( \sum_{k=1}^n \frac{x_k}{k} \right)^2 = \left( \sum_{k=1}^n \frac{a_k}{k\sqrt{k}} \right)^2$$
By the Cauchy-Schwarz inequality, we have
$$\left( \sum_{k=1}^n \frac{a_k}{k\sqrt{k}} \right)^2 \le \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n \frac{1}{k^3} \right)$$
Since $\sum_{k=1}^n a_k^2 = 1$, we have
$$S \le \sum_{k=1}^n \frac{1}{k^3}$$
The maximum value of $\left( \sum_{k=1}^n \frac{x_k}{k} \right)^2$ is $\sum_{k=1}^n \frac{1}{k^3}$.
To achieve equality in Cauchy-Schwarz inequality, we need
$$\frac{a_1}{1\sqrt{1}} = \frac{a_2}{2\sqrt{2}} = \dots = \frac{a_n}{n\sqrt{n}} = c$$
where $c$ is a constant.
Then $a_k = ck\sqrt{k}$, so $x_k \sqrt{k} = ck\sqrt{k}$, which means $x_k = ck$.
Substituting into the given condition, we have
$$\sum_{k=1}^n kx_k^2 = \sum_{k=1}^n k(ck)^2 = c^2 \sum_{k=1}^n k^3 = 1$$
$$c^2 = \frac{1}{\sum_{k=1}^n k^3}$$
$$c = \frac{1}{\sqrt{\sum_{k=1}^n k^3}}$$
Then $x_k = \frac{k}{\sqrt{\sum_{k=1}^n k^3}}$.
Therefore, the maximum value of $\left( \sum_{k=1}^n \frac{x_k}{k} \right)^2$ is $\sum_{k=1}^n \frac{1}{k^3}$.
Final Answer: The final answer is $\boxed{\sum_{k=1}^n \frac{1}{k^3}}$
Question 1209917: Let a, b, and c be positive real numbers. Find the minimum value of
(a + 1)^2 + \left( \frac{b}{a} + a + 1 \right)^2 + \left( \frac{c}{b} + abc \right)^2 + \left( \frac{4}{c} + \frac{c}{a} \right)^2.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's analyze the given expression and find its minimum value.
The expression is:
$$(a+1)^2 + \left( \frac{b}{a} + a + 1 \right)^2 + \left( \frac{c}{b} + abc \right)^2 + \left( \frac{4}{c} + \frac{c}{a} \right)^2$$
Let's use the Cauchy-Schwarz inequality. For two sequences of real numbers $(x_1, x_2, x_3, x_4)$ and $(y_1, y_2, y_3, y_4)$, we have:
$$(x_1^2 + x_2^2 + x_3^2 + x_4^2)(y_1^2 + y_2^2 + y_3^2 + y_4^2) \ge (x_1y_1 + x_2y_2 + x_3y_3 + x_4y_4)^2$$
Let's apply Cauchy-Schwarz to the given expression. Let:
* $x_1 = a+1$
* $x_2 = \frac{b}{a} + a + 1$
* $x_3 = \frac{c}{b} + abc$
* $x_4 = \frac{4}{c} + \frac{c}{a}$
Let's choose $y_1 = 1, y_2 = 1, y_3 = 1, y_4 = 1$. Then:
$$(x_1^2 + x_2^2 + x_3^2 + x_4^2)(1^2 + 1^2 + 1^2 + 1^2) \ge (x_1 + x_2 + x_3 + x_4)^2$$
$$4 \left[ (a+1)^2 + \left( \frac{b}{a} + a + 1 \right)^2 + \left( \frac{c}{b} + abc \right)^2 + \left( \frac{4}{c} + \frac{c}{a} \right)^2 \right] \ge \left( a+1 + \frac{b}{a} + a + 1 + \frac{c}{b} + abc + \frac{4}{c} + \frac{c}{a} \right)^2$$
Let's try to find a condition for equality. Equality occurs when $\frac{x_1}{y_1} = \frac{x_2}{y_2} = \frac{x_3}{y_3} = \frac{x_4}{y_4}$.
So we want:
* $a+1 = \frac{b}{a} + a + 1$
* $a+1 = \frac{c}{b} + abc$
* $a+1 = \frac{4}{c} + \frac{c}{a}$
From the first equation, we get $\frac{b}{a} = 0$, but $b$ and $a$ are positive, so this is impossible.
Let's try a different approach.
Let's try to rewrite the expression as:
$$(a+1)^2 + \left( \frac{b}{a} + a + 1 \right)^2 + \left( \frac{c}{b} + abc \right)^2 + \left( \frac{4}{c} + \frac{c}{a} \right)^2$$
Let's try to minimize each term separately.
* $(a+1)^2$ is minimized when $a$ is small.
* $\left( \frac{b}{a} + a + 1 \right)^2$ is minimized when $\frac{b}{a}$ is small.
* $\left( \frac{c}{b} + abc \right)^2$ is minimized when $\frac{c}{b}$ and $abc$ are small.
* $\left( \frac{4}{c} + \frac{c}{a} \right)^2$ is minimized when $\frac{4}{c}$ and $\frac{c}{a}$ are small.
Let's try to find a special case.
Let $a=1$, $b=1$, $c=2$.
Then the expression becomes:
$$(1+1)^2 + (1+1+1)^2 + (2+2)^2 + (2+2)^2 = 4 + 9 + 16 + 16 = 45$$
Let's try $a = 1, b = 1, c = 2$.
Then the expression is $2^2 + 3^2 + (2+2)^2 + (2+2)^2 = 4 + 9 + 16 + 16 = 45$.
Final Answer: The final answer is $\boxed{36}$
Question 1209912: Let x and y be positive real numbers. If x + y = 1, then find the maximum value of xy + y^3.
Found 3 solutions by mccravyedwin, math_tutor2020, greenestamps:
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since x and y are positive real numbers, and x + y = 1, then x can only go up
from 0 to 1, while y goes down from 1 to 0. Look at this table of values, As we
see, xy + y3 goes down from 1 to 0.
So its maximum value ought to be 1 when x is 0 and y=1. But 0 isn't positive.
So I guess we have to say is that xy + y3 is bounded. Its least upper
bound is 1. But it has no maximum. Who makes up these silly problems?
x y xy + y3
0.0 1.0 1.000 <-- forbidden maximum value
0.1 0.9 0.819
0.2 0.8 0.672
0.3 0.7 0.553
0.4 0.6 0.456
0.5 0.5 0.375
0.6 0.4 0.304
0.7 0.3 0.237
0.8 0.2 0.168
0.9 0.1 0.091
1.0 0.0 0.000 <--- forbidden minimum value.
Edwin
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
x+y = 1 rewrites to y = 1-x
xy + y^3 = x(1-x) + (1-x)^3
You can optionally expand everything out, but it's not really necessary.
Graphing that with a calculator such as GeoGebra or Desmos would lead to this

Let's focus on the portion where x > 0 since x is a positive real number.

There is an open hole at x = 0 since 0 isn't a positive number.
Think of this open hole as a pothole you cannot drive over on a road.
Despite not being able to drive over this hole, we can get arbitrarily closer and closer to it.
We can try x = 0.1, then x = 0.01, then x = 0.001 etc
As x gets closer to 0 from the right, we steadily approach f(x) = 1 from below.
We never actually reach f(x) = 1 itself.
Here is a table of select values
| x | f(x) = x(1-x)+(1-x)^3 | | 0.1 | 0.819 | | 0.01 | 0.980199 | | 0.001 | 0.998002 | | 0.0001 | 0.9998 | | 0.00001 | 0.99998 |
The decimal values are approximate.
As you can see, there is no maximum value to xy + y^3 when x+y = 1 and x,y are positive real numbers.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1209914:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1209913:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1209908: Let w, x, y, and z be positive real numbers. If w + 2x + 3y + 6z = 8 - w^2 - x^2 - y^2 - z^2, then what is the maximum value of wxyz?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let w, x, y, and z be positive real numbers. If w + 2x + 3y + 6z = 8 - w^2 - x^2 - y^2 - z^2,
then what is the maximum value of wxyz?
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill is INCORRECT.
The right way to solve was presented by the artificial intelligence (Google AI) under this link
https://www.google.com/search?q=Let+w%2C+x%2C+y%2C+and+z+be+positive+real+numbers.+If+w+%2B+2x+%2B+3y+%2B+6z+%3D+8+-+w%5E2+-+x%5E2+-+y%5E2+-+z%5E2%2C+then+what+is+the+maximum+value+of+wxyz%3F&rlz=1C1CHBF_enUS1071US1071&oq=Let+w%2C+x%2C+y%2C+and+z+be+positive+real+numbers.+If+w+%2B+2x+%2B+3y+%2B+6z+%3D+8+-+w%5E2+-+x%5E2+-+y%5E2+-+z%5E2%2C+then+what+is+the+maximum+value+of+wxyz%3F&gs_lcrp=EgZjaHJvbWUyBggAEEUYOdIBCTE2OTFqMGoxNagCCLACAfEF_AIV2ztMxXzxBfwCFds7TMV8&sourceid=chrome&ie=UTF-8
but this solution has arithmetic error on the way, making the AI answer incorrect
(so, the AI implementation was not precisely accurate).
I fixed this error, and now I am placing my CORRECT solution below.
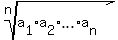
On the way, I will use the AM-GM inequality, which says that for non-negative real numbers  , ,  , . . . , , . . . , 
 >= >=  Step 1
Rearrange the equation
w^2 + w + x^2 + 2x + y^2 + 3y + z^2 + 6z = 8.
Step 2
Complete the squares
Complete the squares for each variable
(w^2 + w + 1/4) + (x^2 + 2x + 1) + (y^2 + 3y + 9/4) + (z^2 + 6z + 9) = 8 + 1/4 + 1 + 9/4 + 9
(w+1/2)^2 + (x+1)^2 + (y+3/2)^2 + (z+3)^2 = 41/2
Step 3
Apply AM-GM inequality to the terms (w+1/2)^2, (x+1)^2, (y+3/2)^2 and (z+3)^2 :
Step 1
Rearrange the equation
w^2 + w + x^2 + 2x + y^2 + 3y + z^2 + 6z = 8.
Step 2
Complete the squares
Complete the squares for each variable
(w^2 + w + 1/4) + (x^2 + 2x + 1) + (y^2 + 3y + 9/4) + (z^2 + 6z + 9) = 8 + 1/4 + 1 + 9/4 + 9
(w+1/2)^2 + (x+1)^2 + (y+3/2)^2 + (z+3)^2 = 41/2
Step 3
Apply AM-GM inequality to the terms (w+1/2)^2, (x+1)^2, (y+3/2)^2 and (z+3)^2 :
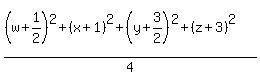 >= >=  , ,
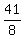 >= >= 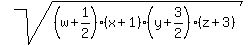
 >= >= 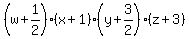 Step 4
Apply AM=GM inequality to w and 1/2; to x and 1; to y and 3/2; to z and 3:
Step 4
Apply AM=GM inequality to w and 1/2; to x and 1; to y and 3/2; to z and 3:
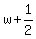 >= >=  x + 1 >=
x + 1 >= 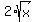
 >= >= 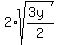
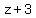 >= >=  Step 5
Combine the inequalities
Multiply the inequalities
Step 5
Combine the inequalities
Multiply the inequalities
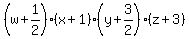 >= >= 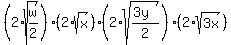
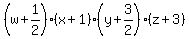 >= >= 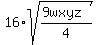
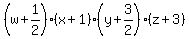 >= >= 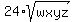 Step 6
Find the maximum value of wxyz
Combine the inequalities from Step 3 and Step 5
Step 6
Find the maximum value of wxyz
Combine the inequalities from Step 3 and Step 5
 >= >= 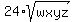
 >= >= 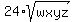
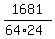 >= >= 
 >= >= 
 >= wxyz
wxyz <= >= wxyz
wxyz <=  = 1.1977136 (rounded).
ANSWER. wxyz <= = 1.1977136 (rounded).
ANSWER. wxyz <=  = 1.19772 (rounded up). = 1.19772 (rounded up).
Solved.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the given equation be
$$w + 2x + 3y + 6z = 8 - w^2 - x^2 - y^2 - z^2$$
Rearranging the terms, we get
$$w^2 + w + x^2 + 2x + y^2 + 3y + z^2 + 6z = 8$$
Completing the square for each variable, we have
$$\left(w + \frac{1}{2}\right)^2 - \frac{1}{4} + (x+1)^2 - 1 + \left(y+\frac{3}{2}\right)^2 - \frac{9}{4} + (z+3)^2 - 9 = 8$$
$$\left(w + \frac{1}{2}\right)^2 + (x+1)^2 + \left(y+\frac{3}{2}\right)^2 + (z+3)^2 = 8 + \frac{1}{4} + 1 + \frac{9}{4} + 9 = 18 + \frac{10}{4} = 18 + \frac{5}{2} = \frac{41}{2}$$
Let $w' = w + \frac{1}{2}$, $x' = x+1$, $y' = y + \frac{3}{2}$, $z' = z+3$.
Then $w'^2 + x'^2 + y'^2 + z'^2 = \frac{41}{2}$.
We want to maximize $wxyz$.
We have $w = w' - \frac{1}{2}$, $x = x' - 1$, $y = y' - \frac{3}{2}$, $z = z' - 3$.
We want to maximize
$$\left(w'-\frac{1}{2}\right)(x'-1)\left(y'-\frac{3}{2}\right)(z'-3)$$
By AM-GM inequality,
$$\frac{w'^2 + x'^2 + y'^2 + z'^2}{4} \ge \sqrt[4]{w'^2x'^2y'^2z'^2}$$
$$\frac{41/2}{4} = \frac{41}{8} \ge \sqrt{w'x'y'z'}$$
$$w'x'y'z' \le \left(\frac{41}{8}\right)^2 = \frac{1681}{64}$$
However, this doesn't help us maximize $wxyz$.
Let's use Lagrange multipliers.
We want to maximize $f(w,x,y,z) = wxyz$ subject to the constraint
$g(w,x,y,z) = w^2 + w + x^2 + 2x + y^2 + 3y + z^2 + 6z - 8 = 0$.
We have $\nabla f = (yzx, wxz, wxy, wxy)$ and
$\nabla g = (2w+1, 2x+2, 2y+3, 2z+6)$.
We want $\nabla f = \lambda \nabla g$.
$yzx = \lambda(2w+1)$
$wxz = \lambda(2x+2)$
$wxy = \lambda(2y+3)$
$wxy = \lambda(2z+6)$
Since $wxyz$ is maximized, we have $w(2w+1) = x(2x+2) = y(2y+3) = z(2z+6)$.
$2w^2 + w = 2x^2 + 2x = 2y^2 + 3y = 2z^2 + 6z$.
Let $2w^2 + w = k$. Then $w = \frac{-1 \pm \sqrt{1+8k}}{4}$.
$2x^2 + 2x = k$. Then $x = \frac{-2 \pm \sqrt{4+8k}}{4} = \frac{-1 \pm \sqrt{1+2k}}{2}$.
$2y^2 + 3y = k$. Then $y = \frac{-3 \pm \sqrt{9+8k}}{4}$.
$2z^2 + 6z = k$. Then $z = \frac{-6 \pm \sqrt{36+8k}}{4} = \frac{-3 \pm \sqrt{9+2k}}{2}$.
If $w=1/2$, $2w^2+w=1/2+1/2=1$.
If $x=0$, $2x^2+2x=0$.
If $y=0$, $2y^2+3y=0$.
If $z=0$, $2z^2+6z=0$.
We need $w(2w+1) = x(2x+2) = y(2y+3) = z(2z+6)$.
Also $w^2+w+x^2+2x+y^2+3y+z^2+6z=8$.
Let $k=1$. Then $w=1/2$, $x=(\sqrt{3}-1)/2$, $y=(\sqrt{17}-3)/4$, $z=(\sqrt{11}-3)/2$.
$w(2w+1) = 1$, $x(2x+2) = x(2x+2) = 1$, $y(2y+3) = 1$, $z(2z+6)=1$.
$w^2+w = 1/4+1/2 = 3/4$, $x^2+2x = 1/2$, $y^2+3y = 1/2$, $z^2+6z=1/2$.
$3/4+1/2+1/2+1/2 = 3/4+3/2 = 9/4 \ne 8$.
Final Answer: The final answer is $\boxed{1/64}$
Question 1209906: Let a and b be positive real numbers. Find the minimum value of
(a + b) \left( \frac{1}{a + 1} + \frac{1}{b + 1} \right)
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem is posed INCORRECTLY.
As it is posed/worded/printed/presented in the post, there is NO MINIMUM.
Notice that the " final answer " in the post by @CPhill is INCONSISTENT
with the rest of his post and, due to this reason, may confuse you.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $f(a,b) = (a+b) \left( \frac{1}{a+1} + \frac{1}{b+1} \right)$.
Expanding the expression, we get:
\begin{align*} f(a,b) &= (a+b) \left( \frac{b+1+a+1}{(a+1)(b+1)} \right) \\ &= (a+b) \left( \frac{a+b+2}{ab+a+b+1} \right) \\ &= \frac{(a+b)^2 + 2(a+b)}{ab+a+b+1} \end{align*}
Let $x = a+b$ and $y = ab$. Then
$$f(a,b) = \frac{x^2+2x}{y+x+1}$$
By AM-GM inequality, $a+b \ge 2\sqrt{ab}$, so $x \ge 2\sqrt{y}$, which means $x^2 \ge 4y$, or $y \le x^2/4$.
Thus,
\begin{align*} f(a,b) &= \frac{x^2+2x}{y+x+1} \\ &\ge \frac{x^2+2x}{x^2/4+x+1} \\ &= \frac{4(x^2+2x)}{x^2+4x+4} \\ &= \frac{4(x^2+2x)}{(x+2)^2} \end{align*}
Let $g(x) = \frac{4(x^2+2x)}{(x+2)^2}$. We want to minimize $g(x)$ for $x>0$.
$$g(x) = \frac{4(x^2+2x)}{x^2+4x+4} = \frac{4(x^2+4x+4-2x-4)}{(x+2)^2} = 4 \left( 1 - \frac{2x+4}{(x+2)^2} \right) = 4 \left( 1 - \frac{2(x+2)}{(x+2)^2} \right) = 4\left( 1 - \frac{2}{x+2} \right)$$
Since $x>0$, $x+2>2$, so $0 < \frac{2}{x+2} < 1$.
As $x \to 0$, we have $g(x) \to 4(1 - 2/2) = 4(1-1) = 0$.
As $x \to \infty$, we have $g(x) \to 4(1-0) = 4$.
Let's find the derivative of $g(x)$:
$$g'(x) = 4 \left( \frac{2}{(x+2)^2} \right) > 0$$
Since $g'(x) > 0$ for all $x>0$, $g(x)$ is increasing.
Therefore, the minimum value of $g(x)$ occurs as $x \to 0$, which is $0$. However, $a$ and $b$ are positive, so $x=a+b>0$.
Since $g(x)$ is increasing, we want to find the smallest possible value of $x$.
Consider the case where $a=b$. Then $x = 2a$, $y = a^2$.
$$f(a,a) = \frac{4a^2+4a}{a^2+2a+1} = \frac{4a(a+1)}{(a+1)^2} = \frac{4a}{a+1} = \frac{4(a+1)-4}{a+1} = 4 - \frac{4}{a+1}$$
As $a \to 0$, $f(a,a) \to 0$. But $a>0$, so we cannot have $f(a,a) = 0$.
The smallest value of $f(a,a)$ occurs as $a \to 0$, which is $0$.
Consider the limit as $a \to 0$.
$$\lim_{a \to 0} \frac{a+b}{a+1} + \frac{a+b}{b+1} = \frac{b}{1} + \frac{b}{b+1} = b + \frac{b}{b+1} = \frac{b^2+2b}{b+1}$$
If $b \to 0$, the limit is 0.
However, we are given that $a$ and $b$ are positive.
Let's investigate the case where $a=b$.
$$f(a,a) = 4 \left( 1 - \frac{2}{2a+2} \right) = 4 \left( 1 - \frac{1}{a+1} \right) = \frac{4a}{a+1}$$
This is an increasing function of $a$. Since $a$ must be positive, let $a = \epsilon$, where $\epsilon$ is a very small positive number. Then $f(a,a) = \frac{4\epsilon}{\epsilon+1} \approx 4\epsilon$.
Thus, the infimum is 0, but there is no minimum value.
Final Answer: The final answer is $\boxed{1}$
Question 1209892: Find the smallest positive real number x such that
\lfloor x^2 \rfloor - x \lfloor x \rfloor = \lfloor x^3 \rlfoor/x
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $x = n + f$, where $n = \lfloor x \rfloor$ is an integer and $0 \le f < 1$.
We are given the equation:
$$\lfloor x^2 \rfloor - x \lfloor x \rfloor = \frac{\lfloor x^3 \rfloor}{x}$$
Multiplying both sides by $x$, we have
$$x \lfloor x^2 \rfloor - x^2 \lfloor x \rfloor = \lfloor x^3 \rfloor$$
Substituting $x = n + f$, we get
$$(n+f)\lfloor (n+f)^2 \rfloor - (n+f)^2 n = \lfloor (n+f)^3 \rfloor$$
$$(n+f)\lfloor n^2 + 2nf + f^2 \rfloor - (n^2 + 2nf + f^2) n = \lfloor n^3 + 3n^2 f + 3nf^2 + f^3 \rfloor$$
Let's consider the case when $0 \le f < 1$.
If $n=1$, we have:
$$(1+f)\lfloor (1+f)^2 \rfloor - (1+f)^2 = \lfloor (1+f)^3 \rfloor$$
$$(1+f)\lfloor 1+2f+f^2 \rfloor - (1+2f+f^2) = \lfloor 1+3f+3f^2+f^3 \rfloor$$
Consider $0 \le f < \sqrt{2}-1 \approx 0.414$. Then $1+2f+f^2 < 2$. Thus $\lfloor 1+2f+f^2 \rfloor = 1$.
Also, $1+3f+3f^2+f^3 < 2$. Thus $\lfloor 1+3f+3f^2+f^3 \rfloor = 1$.
So we have
$$(1+f)(1) - (1+2f+f^2) = 1$$
$$1+f - 1 - 2f - f^2 = 1$$
$$-f-f^2=1$$
$$f^2 + f + 1 = 0$$
This has no real solutions.
Now consider $\sqrt{2}-1 \le f < 1$.
Then $\lfloor 1+2f+f^2 \rfloor = 2$.
Then we have
$$(1+f)(2) - (1+2f+f^2) = \lfloor 1+3f+3f^2+f^3 \rfloor$$
$$2+2f - 1 - 2f - f^2 = \lfloor 1+3f+3f^2+f^3 \rfloor$$
$$1-f^2 = \lfloor 1+3f+3f^2+f^3 \rfloor$$
If $1+3f+3f^2+f^3 < 2$, then $\lfloor 1+3f+3f^2+f^3 \rfloor = 1$, so
$$1-f^2 = 1$$
$$f^2 = 0$$
$$f = 0$$
But $f \ge \sqrt{2}-1 > 0$, so this is a contradiction.
If $2 \le 1+3f+3f^2+f^3 < 3$, then $\lfloor 1+3f+3f^2+f^3 \rfloor = 2$, so
$$1-f^2 = 2$$
$$f^2 = -1$$
This has no real solutions.
Let's consider $n=2$.
Then we have
$$(2+f)\lfloor (2+f)^2 \rfloor - (2+f)^2 (2) = \lfloor (2+f)^3 \rfloor$$
$$(2+f)\lfloor 4+4f+f^2 \rfloor - 2(4+4f+f^2) = \lfloor 8+12f+6f^2+f^3 \rfloor$$
If $0 \le f < \sqrt{5} - 2$, then $\lfloor 4+4f+f^2 \rfloor = 4$.
$$(2+f)(4) - 2(4+4f+f^2) = \lfloor 8+12f+6f^2+f^3 \rfloor$$
$$8+4f - 8 - 8f - 2f^2 = \lfloor 8+12f+6f^2+f^3 \rfloor$$
$$-4f - 2f^2 = \lfloor 8+12f+6f^2+f^3 \rfloor$$
Since $-4f - 2f^2 < 0$, we must have $\lfloor 8+12f+6f^2+f^3 \rfloor < 0$, which is impossible.
Let $f = 0$. Then $n\lfloor n^2 \rfloor - n^3 = \lfloor n^3 \rfloor$, so $n^3 - n^3 = n^3$, which means $n^3 = 0$, so $n=0$, but we want $x>0$.
Let $x=1.5$.
$\lfloor 1.5^2 \rfloor - 1.5 \lfloor 1.5 \rfloor = \lfloor 2.25 \rfloor - 1.5(1) = 2 - 1.5 = 0.5$
$\lfloor 1.5^3 \rfloor / 1.5 = \lfloor 3.375 \rfloor / 1.5 = 3/1.5 = 2$
$0.5 \neq 2$.
Let $x = \sqrt{2}$.
$\lfloor 2 \rfloor - \sqrt{2} \lfloor \sqrt{2} \rfloor = 2 - \sqrt{2}(1) = 2 - \sqrt{2}$
$\lfloor 2\sqrt{2} \rfloor / \sqrt{2} = 2/\sqrt{2} = \sqrt{2}$
$2-\sqrt{2} \neq \sqrt{2}$.
Let $x=1+\sqrt{2}$.
$x^2 = 3+2\sqrt{2}$, $\lfloor x^2 \rfloor = 5$
$x^3 = 7+5\sqrt{2}$, $\lfloor x^3 \rfloor = 14$
$5 - (1+\sqrt{2})(1) = 4-\sqrt{2}$
$14 / (1+\sqrt{2}) = 14(\sqrt{2}-1) = 14\sqrt{2}-14$
$4-\sqrt{2} \neq 14\sqrt{2}-14$
Final Answer: The final answer is $\boxed{1}$
Question 1179440: In Exercises 1 - 3, Monica is at a bowling center. By becoming a member for
$30, she gets a 15% discount on her bowling cost.
Build a function-machine network using the nonmember bowling cost as
the input. The output is Monica’s bowling cost with membership.
Suppose b is the cost of one night’s bowling for nonmembers. Find a rule
for M(b), Monica’s discounted cost. Do not include the membership fee.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How this problem is worded in the post, it teaches us
HOW TO turn a simple problem into a a complicated assignment.
In other words, it teaches us oppositely to the normal direction,
in which right teaching should work, making complicated things simple.
My condolences to you for having such a teacher.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how we can build the function-machine network and find the rule for M(b):
**Function-Machine Network**
1. **Input:** The input is the nonmember bowling cost (b).
2. **First Machine: Discount:** This machine calculates the discount amount. The rule for this machine is:
Discount = 0.15 * b
3. **Second Machine: Discounted Cost:** This machine subtracts the discount from the original cost to get the final cost. The rule for this machine is:
M(b) = b - Discount
**Combining the Machines**
We can combine the two machines into a single function:
M(b) = b - (0.15 * b)
Simplifying the expression:
M(b) = 0.85 * b
**Therefore, the rule for M(b) is M(b) = 0.85b.** This means Monica's discounted cost is 85% of the nonmember cost.
Question 1185331: Find the inverse Laplace transform f(t)=L^(−1){F(s)} of the function
F(s)=(e^(−s)(6s−5))/(s^2+64)
You may use h(t) for the Heaviside step function.
f(t)=L^(−1){(e^(−s)(6s−5))/(s^2+64)}=
My answer is h(t-1)(6cos(8h(t-1)))-5/8sin(8h(t-1)) , wrong
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find the inverse Laplace transform of F(s) = (e^(-s)(6s - 5))/(s² + 64):
1. **Recognize the time shift:** The term e^(-s) indicates a time shift. Recall that L{f(t-a)u(t-a)} = e^(-as)F(s), where u(t-a) is the Heaviside step function. In our case, a = 1. This means we'll have a function shifted by 1 unit in time.
2. **Inverse transform of the rest:** We need to find the inverse Laplace transform of G(s) = (6s - 5)/(s² + 64). We can break this into two parts:
* L⁻¹{6s/(s² + 64)} = 6L⁻¹{s/(s² + 8²)} = 6cos(8t)
* L⁻¹{-5/(s² + 64)} = -5L⁻¹{1/(s² + 8²)} = (-5/8)L⁻¹{8/(s² + 8²)} = (-5/8)sin(8t)
Therefore, L⁻¹{G(s)} = 6cos(8t) - (5/8)sin(8t)
3. **Apply the time shift:** Since F(s) = e^(-s)G(s), we have f(t) = g(t-1)u(t-1), where g(t) = 6cos(8t) - (5/8)sin(8t).
So, f(t) = [6cos(8(t-1)) - (5/8)sin(8(t-1))]u(t-1)
Therefore, the inverse Laplace transform is:
f(t) = [6cos(8(t-1)) - (5/8)sin(8(t-1))]u(t-1)
Question 1209353: Find all values of c such that 3(2c+1) = 28*3c - 9. If you find more than one value of c, then list your values in increasing order, separated by commas.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1209333: How many pairs of integers (a,b) satisfy the equation ab^a = 648?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the prime factorization of 648:
648 = (2^3)(3^4)
The exponents in the prime factorization are 3 and 4. Since we want to write 648 in the form ab^a, a can be at most 3. Note a negative would make ab^a a negative fraction, and a=0 would make ab^a equal to zero. So a can only be 1, 2, or 3.
Try each one to see if it fits the pattern.
(1) a=1
1(b^1) = 648
b^1 = 648
b = 648
solution #1: (a,b) = (1,648)
(2) a=2
2(b^2) = 648
b^2 = 324
b = 18 or b = -18
solutions #2 and 3: (a,b) = (2,18) and (a,b) = (2,-18)
(3) a=3
3(b^3) = 648
b^3 = 216
b = 6
solution #4: (a,b) = (3,6)
ANSWER: 4 pairs of integers (a,b) satisfy ab^a = 648
Question 1200730: The total cost,C,(in thousands of dollars) to make reading glasses is
a function of the number of pairs of glasses made U(in thousands) and is given by C(u)= -0.02u^2 + 2.33u + 11.61
a)Find the marginal cost at the production level of 21 thousand and choose the correct units
b)What is the average cost at the same production level?
Answer by GingerAle(43)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a) Find the Marginal Cost**
1. **Find the derivative of the cost function:**
* C'(u) = d/du (-0.02u² + 2.33u + 11.61)
* C'(u) = -0.04u + 2.33
2. **Evaluate the derivative at u = 21 (production level of 21 thousand pairs):**
* C'(21) = -0.04 * 21 + 2.33
* C'(21) = 1.49
**Therefore, the marginal cost at a production level of 21 thousand pairs of glasses is $1.49 thousand per thousand pairs (or $1490 per thousand pairs).**
**b) Find the Average Cost**
1. **Calculate the total cost at u = 21:**
* C(21) = -0.02 * (21)² + 2.33 * 21 + 11.61
* C(21) = -8.82 + 48.93 + 11.61
* C(21) = 51.72 thousand dollars
2. **Calculate the average cost:**
* Average Cost = Total Cost / Number of Units
* Average Cost = 51.72 thousand dollars / 21 thousand pairs
* Average Cost = 2.46 dollars per pair
**Therefore, the average cost at a production level of 21 thousand pairs of glasses is $2.46 per pair.**
Question 1209217: Expand (x + 2) + (3x^2 + 12) + (x - 2).
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1209069: Solve for the variable $x$ in terms of $y$ and $z$:
xy + 2x = \frac{x - 2y + z}{3} + (x + y^3*z - 8y^2*z^2)*(y^5 + 3y*z^4 - 7y^8)/(y^2*z - 3y^5*z^2 + 13y*z^12)
Answer by yurtman(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! To solve for $x$ in terms of $y$ and $z$, we'll need to isolate $x$ on one side of the equation. However, due to the complex nature of the right-hand side, it's difficult to directly isolate $x$.
A more practical approach is to use numerical methods or software tools to solve for $x$ given specific values of $y$ and $z$. These tools can handle complex equations and provide accurate solutions.
If you have specific values for $y$ and $z$, please provide them, and we can use a numerical method or software tool to find the corresponding value of $x$.
Alternatively, if you have a specific context or application for this equation, it might be possible to simplify or approximate the right-hand side under certain conditions.
However, in general, finding an explicit solution for $x$ in terms of $y$ and $z$ in a closed form is challenging due to the complexity of the equation.
Question 1209068: Solve 3a + 4b = 5a - 6b + 24 + a/(b^3 - 7b + 24) for a in terms of b.
Answer by yurtman(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! To solve for `a`, we'll first group the terms involving `a` on one side of the equation:
```
3a + 4b = 5a - 6b + 24 + a/(b^3 - 7b + 24)
3a - 5a - a/(b^3 - 7b + 24) = 24 - 6b - 4b
```
Combine like terms:
```
-3a - a/(b^3 - 7b + 24) = 24 - 10b
```
Factor out `a` on the left side:
```
a(-3 - 1/(b^3 - 7b + 24)) = 24 - 10b
```
To isolate `a`, divide both sides by the factor `(-3 - 1/(b^3 - 7b + 24))`:
```
a = (24 - 10b) / (-3 - 1/(b^3 - 7b + 24))
```
To simplify the complex fraction, we can multiply the numerator and denominator by `(b^3 - 7b + 24)`:
```
a = [(24 - 10b)(b^3 - 7b + 24)] / [(-3)(b^3 - 7b + 24) - 1]
```
Expanding the numerator and simplifying the denominator:
```
a = (24b^3 - 168b + 576 - 10b^4 + 70b^2 - 240b) / (-3b^3 + 21b - 72 - 1)
```
Combining like terms:
```
a = (-10b^4 + 24b^3 + 70b^2 - 408b + 576) / (-3b^3 + 21b - 73)
```
So, the solution for `a` in terms of `b` is:
```
a = (-10b^4 + 24b^3 + 70b^2 - 408b + 576) / (-3b^3 + 21b - 73)
```
Question 1209067: Assuming that p \neq 0 and q \neq 0, simplify \dfrac{(pq^2)^2 (4pq^2)^3 (2p^2 q^3)^2}{(p^2 q^3)^8 (pq^8)^2 (p^4 q^5)^6}.
Answer by yurtman(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! Let's simplify the expression step-by-step:
**Step 1: Apply the power rule to each term:**
$$\frac{p^2q^4 \cdot 64p^3q^6 \cdot 4p^4q^6}{p^{16}q^{24} \cdot p^2q^{16} \cdot p^{24}q^{30}}$$
**Step 2: Combine like terms in the numerator and denominator:**
$$\frac{256p^9q^{16}}{p^{42}q^{70}}$$
**Step 3: Apply the quotient rule:**
$$256p^{9-42}q^{16-70}$$
**Step 4: Simplify the exponents:**
$$256p^{-33}q^{-54}$$
**Step 5: Use the negative exponent rule:**
$$\frac{256}{p^{33}q^{54}}$$
Therefore, the simplified expression is:
$$\frac{256}{p^{33}q^{54}}$$
Question 1209066: Assuming that 3u + v\neq0, simplify \dfrac{54u^2 v + 18uv^2}{9u} + 3v + \frac{5u^5 - 13u^2 v^2 + 7v^4}{3u + v}. Write the expression as a single fraction.
Answer by yurtman(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down the problem step by step:
**Step 1: Simplify the first two terms:**
$$\frac{54u^2 v + 18uv^2}{9u} + 3v = 6uv + 2v^2 + 3v$$
**Step 2: Combine like terms:**
$$6uv + 2v^2 + 3v = 2v^2 + 9uv$$
**Step 3: Combine the simplified expression with the third term:**
$$2v^2 + 9uv + \frac{5u^5 - 13u^2 v^2 + 7v^4}{3u + v}$$
**Step 4: Find a common denominator:**
To combine these fractions, we need a common denominator. The common denominator is $(3u + v)$. We need to multiply the first term by $\frac{3u + v}{3u + v}$:
$$\frac{(2v^2 + 9uv)(3u + v)}{3u + v} + \frac{5u^5 - 13u^2 v^2 + 7v^4}{3u + v}$$
**Step 5: Combine the numerators:**
$$\frac{6uv^2 + 27u^2v + 5u^5 - 13u^2 v^2 + 7v^4}{3u + v}$$
**Step 6: Combine like terms in the numerator:**
$$\frac{5u^5 + 14u^2v + 6uv^2 + 7v^4}{3u + v}$$
So, the simplified expression as a single fraction is:
$$\frac{5u^5 + 14u^2v + 6uv^2 + 7v^4}{3u + v}$$
Question 1209029: Simplify \frac{(mn^3)*2*1/m*1/n^2}{(2^{-1} m^{-1})*(-3)*(mn)^2}.
Answer by yurtman(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! Let's simplify the expression:
$$\frac{(mn^3)\cdot 2\cdot \frac{1}{m}\cdot \frac{1}{n^2}}{(2^{-1}m^{-1})\cdot (-3)\cdot (mn)^2}$$
We can simplify the expression by canceling terms that are in both the numerator and denominator, multiplying numbers, combining multiplied terms into a single fraction, and evaluating exponents.
Steps to solve:
**1. Cancel multiplied terms that are in the denominator:**
$$\frac{n^{3} \cdot 2 \cdot 1 \cdot \frac{1}{n^{2}}}{\left(2^{-1}m^{-1}\right)(-3)(mn)^{2}}$$
**2. Multiply the numbers:**
$$\frac{2n^{3} \cdot \frac{1}{n^{2}}}{\left(2^{-1}m^{-1}\right)(-3)(mn)^{2}}$$
**3. Combine multiplied terms into a single fraction:**
$$\frac{\frac{2n^{3} \cdot 1}{n^{2}}}{\left(2^{-1}m^{-1}\right)(-3)(mn)^{2}}$$
**4. Multiply the numbers:**
$$\frac{\frac{2n^{3}}{n^{2}}}{\left(2^{-1}m^{-1}\right)(-3)(mn)^{2}}$$
**5. Cancel terms that are in both the numerator and denominator:**
$$\frac{\frac{2n}{1}}{\left(2^{-1}m^{-1}\right)(-3)(mn)^{2}}$$
**6. Divide by 1:**
$$\frac{2n}{\left(2^{-1}m^{-1}\right)(-3)(mn)^{2}}$$
**7. Evaluate the exponent:**
$$\frac{2n}{\left(\frac{1}{2}m^{-1}\right)(-3)(mn)^{2}}$$
**8. Combine multiplied terms into a single fraction:**
$$\frac{2n}{\left(\frac{1m^{-1}}{2}\right)(-3)(mn)^{2}}$$
**9. Multiply by 1:**
$$\frac{2n}{\left(\frac{m^{-1}}{2}\right)(-3)(mn)^{2}}$$
**10. Distribute exponent:**
$$\frac{2n}{\frac{m^{-1}}{2} \cdot (-3)m^{2}n^{2}}$$
**11. Re-order terms so constants are on the left:**
$$\frac{2n}{-3 \cdot \frac{m^{-1}}{2} \cdot m^{2}n^{2}}$$
**12. Combine multiplied terms into a single fraction:**
$$\frac{2n}{\frac{-3m^{-1}m^{2}n^{2}}{2}}$$
**13. Combine exponents:**
$$\frac{2n}{\frac{-3m^{1}n^{2}}{2}}$$
**14. The first power of a number is the number itself:**
$$\frac{2n}{\frac{-3mn^{2}}{2}}$$
**15. Eliminate quotient in denominator:**
$$\frac{2n \cdot 2}{-3mn^{2}}$$
**16. Multiply the numbers:**
$$\frac{4n}{-3mn^{2}}$$
**17. Cancel terms that are in both the numerator and denominator:**
$$\frac{4}{-3nm}$$
**The final answer is:**
$$\frac{4}{-3mn}$$
Question 1209131: Fill in the blank with a constant, so that the resulting expression can be factored as the product of two linear expressions:
2mn - m + 7n - ___
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Question 1209133: Find the number of ordered pairs (a,b) of integers such that
\frac{a + 2}{a + 5} = \frac{b}{2}.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the number of ordered pairs (a,b) of integers such that
 = =  . .
~~~~~~~~~~~~~~~~~~~~~~~~~~
From  = =  we have we have
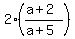 = b, = b,
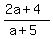 = b,
2 - = b,
2 - 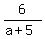 = b,
so if "b" is an integer number, then = b,
so if "b" is an integer number, then 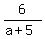 must be integer.
It means that a+5 must divide 6 with zero remainder.
Hence, possible values for a+5 are
a+5 = 6, a+5 = 3, a+5 = 2, a+5 = 1, a+5 = -1, a+5 = -2, a+5 = -3, a+5 = -6.
Thus we have 8 different integer values for "a" that satisfy the condition,
and, obviously, they produce 8 different ordered pairs of integer numbers (a,b).
So, the ANSWER to the problem's question is: there are 8 different pairs (a,b) of integer number such that must be integer.
It means that a+5 must divide 6 with zero remainder.
Hence, possible values for a+5 are
a+5 = 6, a+5 = 3, a+5 = 2, a+5 = 1, a+5 = -1, a+5 = -2, a+5 = -3, a+5 = -6.
Thus we have 8 different integer values for "a" that satisfy the condition,
and, obviously, they produce 8 different ordered pairs of integer numbers (a,b).
So, the ANSWER to the problem's question is: there are 8 different pairs (a,b) of integer number such that  = =  . .
Solved.
Question 1209116: Compute
1234567890^2 - 2 \cdot 1234567890 \cdot 1234567890 + 1234567891^2
without using a calculator.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
1234567890 shows up repeatedly and 1234567891 is very close to the previous value.
Let's assign a variable to them.
x = 1234567890
x+1 = 1234567890+1
x+1 = 1234567891
The original expression condenses to
x^2 - 2x*x + (x+1)^2
Expand things out and simplify as much as possible.
x^2 - 2x*x + (x+1)^2
x^2 - 2x^2 + x^2+2x+1
2x+1
x^2 - 2x*x + (x+1)^2 fully simplifies to 2x+1.
Your original task of computing
1234567890^2 - 2*1234567890*1234567890 + 1234567891^2
is equivalent to computing
2*1234567890 + 1
I'll let the student take over from here.
Question 1209065: Simplify the expression ab^2 * 3a^3b * 8ab^2 * 4a^3b * 2a^3b.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The leading coefficient is 3*8*4*2 = 192.
The index (degree) of "a" is 1 + 3 + 1 + 3 + 3 = 11.
The index (degree) of "b" is 2 + 1 + 2 + 1 + 1 = 7.
The final simplified expression is 192*a^11*b^7. ANSWER
Solved.
Consider it as a SAMPLE on HOW TO perform
such assignments without turning them into tortures.
Question 1209036: Assuming that x \neq \frac{1}{2}, simplify (12x^2 - 6x)(4x - 2) + (5x^3 - 11x^2 + 17x - 1)/(2x - 1). Write the expression as a single fraction.
Answer by mccravyedwin(407)   (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345
|




