SOLUTION: Find the last two digits in the decimal numeral for (3¹⁶⁷)⁹⁵ A) 27 B) 43 C) 81 D) 29 E) 07

(1)  First, let's find two last digits of the number  .


     It is clear, that looking for the last two digits of the number  ,  

     we should track last two digits of the number of 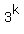  for k = 1, 2, 3, 4, . . . 


     This sequence of the last two digits of numbers {3^k mod 100}  is periodical.  
     The period starts from the first term and the period length is 20, 
     as it can be seen from this table below


     k            1  2  3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19 20 21
     3^k mod 100  3  9 27  81  43  29  87  61  83  49  47  41  23  69   7  21  63  89  67  1  3


     Since 167 = 8*20 + 7, the last two digits of the number  is the 7th term of this 
     cyclic sequence, i.e. the number 87.



(2)  So, now next goal is to determine the last two digits of the number  .


     Again, it is clear, that looking for the last two digits of the number  ,  

     we should track last two digits of the numbers  {{87^k}}}  for k = 1, 2, 3, 4, . . . 


     This sequence of the last two digits of numbers {87^k mod 100}  is periodical.
     The period starts from the first term and the period length is 20, 
     as it can be seen from this table below


     k              1  2  3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19 20 21
     87^k mod 100  87 69  3  61   7   9  83  21  27  49  63  81  47  89  43  21  67  29  23  1 87

     
     Since 95 = 4*20 + 15, the last two digits of the number  is the 15th term of this 
     cyclic sequence, i.e. the number 43.


ANSWER.  The last two digits in the decimal numeral for  (3¹⁶⁷)⁹⁵  are  43.