Question 1131704: Solve 6x⁴ - 35x³ + 62x² - 35x + 6 = 0
Found 4 solutions by rothauserc, MathLover1, ikleyn, MathTherapy:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! 6x^4 - 35x^3 + 62x^2 - 35x + 6 = 0
:
check for the factors of 6(this is the constant and also the leading coefficient in the above equation)
:
use the Rational Zeros Theorem
:
factors for 6 are 1, 2, 3, 6
:
the possible zeros are
:
(+ or - 1, 2, 3, 6)/(1, 2, 3, 6) = + or - 1, 2, 3, 6, 1/2, 1, 3/2, 3, 1/3, 2/3, 1, 2, 1/6, 1/3, 1/2, 1 =
:
-6, -3, -2, -3/2, -1, -1/2, -2/3, -1/3, -1/6, 1/6, 1/3, 2/3, 1/2, 1, 3/2, 2, 3, 6
:
look at the graph to see if we can eliminate any of the possible zeros
:

:
from the graph we see that there are no negative roots and 4 positive roots
:
we can eliminate 1/6, 2/3, 1, 3/2, 6
:
*******************************************************
the roots are 1/3, 1/2, 2, 3
:
to check this substitute for x in the equation
*******************************************************
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This equation of the degree 4 is VERY SPECIAL.
It relates to the class of so named palindromic equations of the degree 4, which means that its coefficients
form a palindromic sequence.
See this Wikipedia article https://en.wikipedia.org/wiki/Reciprocal_polynomial#Palindromic_polynomial
There is a SPECIAL PROCEDURE in algebra to solve such equations. It is presented below.
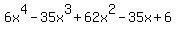 = 0 (1)
It follows from the equation that x= 0 IS NOT the root.
So, we can divide both sides by = 0 (1)
It follows from the equation that x= 0 IS NOT the root.
So, we can divide both sides by  without loosing the roots. In this way, you will get an equivalent equation without loosing the roots. In this way, you will get an equivalent equation
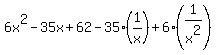 = 0.
Group and re-write it equivalently in the form = 0.
Group and re-write it equivalently in the form
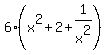 - - 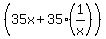 + 50 = 0, or + 50 = 0, or
 - - 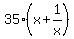 + 50 = 0. (2)
Introduce new variable u = + 50 = 0. (2)
Introduce new variable u =  + +  . Then equation (2) takes a form . Then equation (2) takes a form
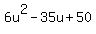 = 0.
Solve this quadratic equation using the quadratic formula = 0.
Solve this quadratic equation using the quadratic formula
 = =  = = 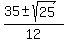 .
The two roots are .
The two roots are
 = = 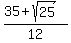 = = 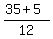 = = 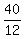 = =  and and
 = = 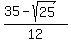 = = 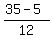 = = 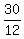 = =  .
Now, to find x, we need to solve two equations
a) .
Now, to find x, we need to solve two equations
a)  + +  = =  and b) and b)  + +  = =  .
Case a). .
Case a).  + +  = = 
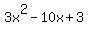 = 0 = 0
 = = 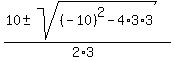 = =  = =  .
So, the two roots are .
So, the two roots are  = =  = 3 and = 3 and  = = 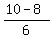 = =  .
Case b). .
Case b).  + +  = = 
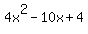 = 0 = 0
 = = 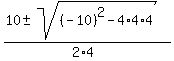 = = 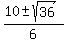 = = 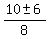 .
So, the two roots are .
So, the two roots are  = =  = 2 and = 2 and  = = 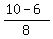 = =  .
ANSWER. The four roots are .
ANSWER. The four roots are  , ,  , 2 and 3. , 2 and 3.
Solved.
The lesson to learn
From this post learn on how to solve palindromic equations.
Every palindromic equation of the degree 4 can be solved in this way.
The major steps of the solution are :
a) Divide both sides by  ;
b) Introduce new variable u = x + ;
b) Introduce new variable u = x +  ;
c) Reduce the equation to a quadratic equation relative new variable u and solve it getting two roots ;
c) Reduce the equation to a quadratic equation relative new variable u and solve it getting two roots  and and  ;
d) Then find x by solving two equations ;
d) Then find x by solving two equations 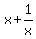 = =  and and 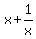 = =  . .
Again :
Every palindromic equation of the degree 4 can be solved in this way.
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Solve 6x⁴ - 35x³ + 62x² - 35x + 6 = 0
RATIONAL ROOT THEOREM produces 2 zeroes: 2 and 3. Therefore, 2 of the expression's factors are: (x - 2) and (x - 3).
FOILing these 2 factors results in trinomial: x2 - 5x + 6
Now, when 6x4 - 35x3 + 62x2 - 35x + 6 is divided by x2 - 5x + 6, we get: 6x2 - 5x + 1. Factoring 6x2 - 5x + 1 gives us: (3x - 1)(2x - 1).
Therefore, 6x4 - 35x3 + 62x2 - 35x + 6 = 0 becomes: (3x - 1)(2x - 1)(x - 2)(x - 3) = 0 and the solutions are: 
|
|
|