Questions on Algebra: Exponents and operations on exponents answered by real tutors!

Tutors Answer Your Questions about Exponents (FREE)

Question 1198080: Find the periodic payments PMT necessary to accumulate the given amount in an annuity account. (Assume end-of-period deposits and compounding at the same intervals as deposits. Round your answer to the nearest cent.)
$50,000 in a fund paying 5% per year, with monthly payments for 5 years, if the fund contains $10,000 at the start
Found 2 solutions by ikleyn, ElectricPavlov:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
The periodic payments PMT necessary to accumulate the given amount in an annuity account.
(Assume end-of-period deposits and compounding at the same intervals as deposits).
$50,000 in a fund paying 5% per year, with monthly payments for 5 years, if the fund contains $10,000 at the start.
~~~~~~~~~~~~~~~~~~~~~~~~~~~

Let solve the problem in 2 steps. Step 1 The future value of the initial amount of $10,000 in 5 years will be 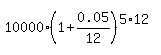= = 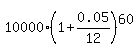12,833.59 dollars. Thus, making monthly deposits of X dollars, we should accrue the rest 50000 - 12833.59 = 37166.41 dollars in 5 years, with compounding. Step 2 Now we write the future value equation for an ordinary annuity with the monthly deposits of X dollars, compounded monthly at 5% annual interest 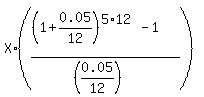= 37166.41, We calculate the factor/multiplier at X separately, and we get this equation X*68.00608284 = 37166.41. Solve for X and get the ANSWER X = 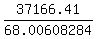= 546.52. At this point, the problem is solved completely. The necessary monthly deposit is 546.52 dollars.

Hip-hip, hurray !

Answer by ElectricPavlov(122)   (Show Source):
You can put this solution on YOUR website!
The periodic payment required to accumulate $50,000 in a fund paying 5% per year with monthly payments for 5 years, starting with an initial balance of $10,000, is approximately **$546.52**.

Question 1046030: Please help me solving
If then the value of
is given by?
Answer by MathTherapy(10551)   (Show Source):
You can put this solution on YOUR website!

Please help me solving If then the value of is given by? --- Applying -- Rationalizing denominator by multiplying numerator and denominator by , the CONJUGATE of the denominator, ===> ===> ===> --- Multiplying numerator and denominator by - 1 --- Applying ----- Substituting for a ====> =====> ===> = 2 <=== , IF

Question 1209868: If 2^{16^x} = 128*4^x, then find 2^x.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
If 2^{16^x} = 128*4^x, then find 2^x.
~~~~~~~~~~~~~~~~~~~~~

Your starting equation is 2^{16^x} = 128*4^x. Notice that 2^(16^x) = 2^(2^(4x)). So, the original equation is equivalent to 2^(2^(4x)) = 2^7 * 2^(2x). It implies for indexes 2^(4x) = 2x + 7. This equation can not be solved algebraically, but it can be solved approximately with reasonable precision using numerical methods and special solvers in the Internet. I used online solver at the site www.desmos.com/calculator. The calculator produced two approximate solutions = -3.49997 (approximately), and = 0.77389 (approximately)             As the reference to the solver' solution, see this link             https://www.desmos.com/calculator/tmxp2wpqt3 Therefore, may have two values = 0.08839 (approx.) and = 1.709874 (approx.) These values, = 0.08838 and = 1.709874, are your ANSWER to the problem's question.

Solved.

Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!

Edwin

Question 1171449: ``The value of function -10000e^(-0.03x)-120x+10000 at its critical points is

Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
To find the value of the function at its critical points, we need to:
1. **Find the derivative of the function.**
2. **Set the derivative equal to zero and solve for x.** This will give us the critical points.
3. **Plug the critical points back into the original function to find the function's value.**
Let's do this step-by-step:
**1. Find the derivative:**
The given function is:
f(x) = -10000e^(-0.03x) - 120x + 10000
The derivative, f'(x), is:
f'(x) = -10000 * (-0.03) * e^(-0.03x) - 120
f'(x) = 300e^(-0.03x) - 120
**2. Set the derivative to zero and solve for x:**
300e^(-0.03x) - 120 = 0
300e^(-0.03x) = 120
e^(-0.03x) = 120 / 300
e^(-0.03x) = 0.4
Take the natural logarithm of both sides:
ln(e^(-0.03x)) = ln(0.4)
-0.03x = ln(0.4)
x = ln(0.4) / -0.03
x ≈ 30.543
**3. Plug the critical point back into the original function:**
f(x) = -10000e^(-0.03x) - 120x + 10000
f(30.543) = -10000e^(-0.03 * 30.543) - 120 * 30.543 + 10000
f(30.543) = -10000e^(-0.91629) - 3665.16 + 10000
f(30.543) = -10000 * 0.4 + 6334.84
f(30.543) = -4000 + 6334.84
f(30.543) = 2334.84
**Therefore, the value of the function at its critical point is approximately 2334.84.**

Question 1209332: For the equation (a-b)^2 + a^2 = 625, a and b are integers and a≥0. List the ordered pairs that occur.
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

The (unordered) pairs of non-negative integers m and n that satisfy the equation m^2+n^2 = 625 are (0,25), (7,24), and (15,20).

In this problem we need to have (a-b)^2+a^2 = 625, with a greater than or equal to 0.

So a can be any of the six numbers in those unordered pairs; and, since (a-b) is squared, (a-b) can be positive or negative.
a (a-b) b ordered pair (a,b) ---------------------------------- 0 25 -25 (0,-25) 0 -25 25 (0,25) 7 24 -17 (7,-17) 7 -24 31 (7,31) 15 20 -5 (15,-5) 15 -20 35 (15,35) 20 15 5 (20,5) 20 -15 35 (20,35) 24 7 17 (24,17) 24 -7 31 (24,31) 25 0 25 (25,0)

Question 1198081: The following table shows the average life expectancies in several countries. Assume that all premiums you calculate are based on end-of-month deposits in a fund yielding 6.8% annual interest compounded monthly to be paid out when a person reaches the life expectancy. HINT [See Example 2.]
Country Japan Canada U.K. U.S. Mexico China India
Life
Expectancy:
Male 80 80 79 76 73 74 64
Life
Expectancy:
Female 87 84 83 81 79 77 68
Calculate the life insurance monthly premium that a 50-year-old female in Japan would pay for a $10,000,000 policy. (Round your answer to the nearest cent.)
Answer by onyulee(41)   (Show Source):
You can put this solution on YOUR website!
**1. Determine the Number of Months**
* Life expectancy for a 50-year-old female in Japan: 87 years
* Years to live: 87 years - 50 years = 37 years
* Number of months to live: 37 years * 12 months/year = 444 months
**2. Calculate the Monthly Interest Rate**
* Annual interest rate: 6.8%
* Monthly interest rate: 6.8% / 12 = 0.5667%
**3. Calculate the Future Value of a Single Deposit**
* We need to find the future value of a single deposit that will grow to $10,000,000 in 444 months.
* Use the future value of an ordinary annuity formula:
* FV = P * [(1 + r)^n - 1] / r
* Where:
* FV = Future Value ($10,000,000)
* P = Monthly Premium (unknown)
* r = Monthly interest rate (0.005667)
* n = Number of months (444)
**4. Solve for the Monthly Premium (P)**
* Rearrange the formula to solve for P:
* P = FV * [r / ((1 + r)^n - 1)]
* Substitute the values:
* P = $10,000,000 * [0.005667 / ((1 + 0.005667)^444 - 1)]
* Calculate P:
* P ≈ $10,000,000 * [0.005667 / (15.236 - 1)]
* P ≈ $10,000,000 * [0.005667 / 14.236]
* P ≈ $10,000,000 * 0.000398
* P ≈ $3,980
**Therefore, the monthly premium for a 50-year-old female in Japan for a $10,000,000 life insurance policy would be approximately $3,980.**
**Note:**
* This calculation assumes that the interest rate remains constant over the entire 37-year period, which may not be the case in reality.
* This calculation also assumes that the individual lives exactly to the life expectancy.
* This is a simplified model and actual life insurance premiums are determined by various factors, including health, lifestyle, and other risk factors.
This information is for illustrative purposes only and does not constitute financial advice. Please consult with a qualified financial advisor for personalized guidance.

Question 1209210: 10 to the power of -11
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.

is = = 0.0000000001.

Question 1208443: 8x10 exponent -4 in standard notation

Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!

Question 1208239: A sugar ant is approximately 2 × 10^−3 meters long. If you put 10 million sugar
ants in a line, what is the distance from end to end?
 200 meters
 2,000 meters
 20,000 meters
 200,000 meters
Found 3 solutions by MathTherapy, math_tutor2020, josgarithmetic:
Answer by MathTherapy(10551)   (Show Source):
You can put this solution on YOUR website!

A sugar ant is approximately 2 × 10^−3 meters long. If you put 10 million sugar ants in a line, what is the distance from end to end?  200 meters  2,000 meters  20,000 meters  200,000 meters 2 x 10^{- 3} x 10,000,000 2 x 10^{- 3} x 10⁷ --- Converting 10,000,000 to EXPONENT with base 10 2 x 10^{(- 3 + 7)} ----- Adding EXPONENTS, when multiplying same base 2 x 10⁴ = 2 x 10,000 = 20,000 meters

Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Answer: 20,000 meters

Work Shown

10 million = 10*(1 million)
= 10*10^6
= 10^1*10^6
= 10^(1+6)
= 10^7
In short, 10 million = 10^7.
Or put another way, 10 million = 10,000,000 = 1 followed by 7 zeros. The exponent tells us how many zeros are tacked onto the 1.

a = 2*10^(-3) = length of one ant in meters
b = 10^7 = number of ants
c = a*b = total length, in meters, of that number of ants assuming no gaps or overlaps.
We also assume the ants form a straight line.

c = a*b
c = 2*10^(-3)*10^7
c = 2*10^(-3+7)
c = 2*10^(4)
c = 2*10,000
c = 20,000 meters

Notes:
I used the exponent rule a^b*a^c = a^(b+c).
20,000 meters = 20 kilometers
20 kilometers = 12.4274 miles approximately
20 kilometers = 6,5616.7979 feet approximately
2*10^(-3) meters = 0.002 meters = 2 mm

Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!
MULTIPLY!

---- and I'll let you finish that.

Question 1208304: (6x^2)^-1/6 all divided by (32x^5/2)^-2/5
Answer by mccravyedwin(406)   (Show Source):
You can put this solution on YOUR website!

Edwin

Question 1208150: Given the following table, determine if the function is linear, or nonlinear. If linear, find the slope.

Table

x............f(x)
-2...........1/4
-1...........1/2
0............1
1............2
2............4

Thanks.

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.

Let's calculate values of the slope in two intervals. In the interval [0,1] of x-axis, the slope is p = = = = 1. In the interval [1,2] of x-axis, the slope is q = = = = 2. We see that the slopes are different. Since the slopes at two intervals are different, it is just enough for us to conclude that the given function is nonlinear.

At this point, the problem is solved in full, with complete explanations.

Question 1207521: please evaluate the expression 3a+4b3 when a=6 and 6=2

Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Replace 'a' with 6 and b with 2.
Then use the order of operations PEMDAS to simplify.

=

=

=

=

Therefore, when a = 6 and b = 2

Question 1207258: Simplify
20^10/40^5 20 to the 10th divided by 40 to the 5th
Found 2 solutions by greenestamps, Theo:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

Break the denominator into two parts:

Simplify the powers of 20 in the numerator and denominator:

ANSWER: 10^5, or 100,000

Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website!
20^10 / 40^5 equals:

2^10 * 10^10) / (2^5 * 2^5 * 10^5) equals:

(2^10 * 10^10) / (2^10 * 10^5) equals:

2^10 / 2^10 * 10^10 / 10^5 equals:

10^5 which is equal to 100,000.

you can use your calculator to confirm.

calculator tells you (20^10) / 40^5 = 100,000.

the concepts used are:

(a * b)^x = a^x * b^x

(a^x * b^x) / (a^y * b^y) = (a^x / a^y) * (b^x / b^y)

you can see the first concept in 20^10 = (2 * 10) ^ 10 = 2^10 * 10^20.

you can see the second concept in (2^10 * 10^10) / (2^10 * 10^5) = 2^10 / 2^10 * 10^10 / 10^5.

Question 1206763: Why does a base number to the exponent of zero equals 1?
When a number is multiplied zero times, shouldn't it be zero?
Example: 10 (exponent zero) = 1.

Found 2 solutions by MathTherapy, math_tutor2020:
Answer by MathTherapy(10551)   (Show Source):
You can put this solution on YOUR website!

Why does a base number to the exponent of zero equals 1? When a number is multiplied zero times, shouldn't it be zero? Example: 10 (exponent zero) = 1. Anything DIVIDED by ITSELF, equals 1. SAME result for all other numbers, variables, etc., EXCEPT 0.

Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Use the ^ key to indicate exponents.
Something like 10^2 means "10 squared" aka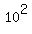
On the keyboard, you find this symbol by holding "shift" then pressing the "6".

If 10^0 = 0 was the case, then multiplying both sides by 10 would get us the following:
10^0 = 0
10*10^0 = 10*0
10^1*10^0 = 0
10^(1+0) = 0 ............ use rule a^b*a^c = a^(b+c)
10^1 = 0
10 = 0
We run into a problem.
The two sides don't agree on the same number, in which we consider the last equation to be false.
The last equation being false makes 10^0 = 0 false.

But if 10^0 = 1 was the case, then we don't have any issues.
10^0 = 1
10*10^0 = 10*1
10^1*10^0 = 10
10^(1+0) = 10
10^1 = 10
10 = 10
The two sides match up to form a true equation at the end.
The true equation at the end leads to a domino effect to make the first equation true.

When going from something like 10^2 to 10^3 we multiply by 10.
Going in reverse from 10^3 to 10^2 we divide by 10.
10^2 to 10^1 is also "divide by 10".
And so on.

Here's a chart of select values.

10^3 1000
10^2 100
10^1 10
10^0 1
10^(-1) 1/10 = 0.1
10^(-2) 1/(10^2) = 1/100 = 0.01
10^(-3) 1/(10^3) = 1/1000 = 0.001

Multiply by 10 to move up the chart.
Divide by 10 to move down the chart.

--------------------------------------------------------------------------

Here is the more general approach using any base b, where b is nonzero.
b^0 = 1
b*b^0 = b*1
b^1*b^0 = b
b^(1+0) = b
b^1 = b
b = b

Once again, b is nonzero.
If b = 0 was the case, then weird things start to happen and that's a very lengthy discussion for another day (and another class).

Question 1206831: Simplyfiy p2-3b
Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!
Already is simplified.
mistyped the exponent?

Question 1206397: Find the value of a/(b^3xc^2) in index form if a = (2/5)^4, b=(-1/3)^3 and c= (3/5)^2
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.

The correct answer is   -.

Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

----------------------

Final answer corrected....

Question 1206369: (16x to the -4 power) to the 2nd power

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.

One of possible interpretations is THIS

= = .

Question 1205815: (-3yx^3)^4

Found 2 solutions by josgarithmetic, MathLover1:
Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!

or

Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website!

=
=
=

Question 1205144: A bacteria culture is started with 100 bacteria. After 7 hours, the population has grown to 600 bacteria. If the population grows exponentially, find the rate of growth in percent
Found 2 solutions by greenestamps, Edwin McCravy:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

Since the problem doesn't specify, I will assume that the percent growth PER HOUR is what the problem is asking for.

In 7 hours the population increases by a factor of 600/100 = 6:

= 1.2917 to 4 decimal places

x = 1.2917-1 = 0.2917

ANSWER: growth rate per hour = 0.2917, or 29.17%

-------------------------------------------------------------------

NOTE: My solution and Edwin's solution are equivalent -- using different definitions of "growth rate":

e^0.2559656385 = 1.291708342

Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!

, or whatever letters your teacher/book uses.
A bacteria culture is started with 100 bacteria.
So A₀ = 100
After 7 hours, the population has grown to 600 bacteria.
A_f = 600 when t = 7
find the rate of growth in percent
About 25.6% Edwin

Question 1204752: If 6^(2x+1) = k, then 6^(4x+3) equals
A 12k
B k^2 + 6
C 6k^2
D 2k + 6
E 36k^2
Found 4 solutions by MathTherapy, math_tutor2020, Edwin McCravy, ikleyn:
Answer by MathTherapy(10551)   (Show Source):
You can put this solution on YOUR website!

If 6^(2x+1) = k, then 6^(4x+3) equals A 12k B k^2 + 6 C 6k^2 D 2k + 6 E 36k^2 , then ----- Substituting

Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Answer: Choice C) 6k^2

-------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------

Work Shown

Method 1

I reached this independently of ikleyn, so there's no citation needed.

---------------------------

Method 2

---------------------------

Method 3

Let
Use graphing software like Desmos or GeoGebra to graph each of the five answer choices A through E as separate functions.
Some teachers will allow graphing tech like that during exams, so it depends on the teacher. Often the app is set to exam mode to be for limited cases. Meaning you won't have access to the CAS feature for instance.

Anyways, set up f(x) = 6^(2x+1) in the first box.
12k for instance would be 12*f(x), k^2+6 would be (f(x))^2 + 6, and so on.
There would be 6 functions defined so far.
As the seventh function, plot 6^(4x+3) to see what curve perfectly aligns to it.
It should be 6*( f(x) )^2

Here's an example comparing answer choice B to 6^(4x+3)
https://www.desmos.com/calculator/kivtpkjz6r
The curves do not overlap, so we can rule choice B out.

However, if we plot choice C and 6^(4x+3) together, then we get this perfect overlap
https://www.desmos.com/calculator/xbdq1rhx20
Click the round button for graph 7 to turn it off, then click it back on. Repeatedly do this to have the curve blink two different colors to show the overlap.

---------------------------

Method 4

We'll use graphing software similar to method 3.
Define f(x) = 6^(2x+1)
Then
A(x) = 12*f(x)
B(x) = (f(x))^2+6
C(x) = 6*(f(x))^2
D(x) = 2*f(x)+6
E(x) = 36*(f(x))^2
are the five answer choices, and we want to check against
G(x) = 6^(4x+3)
To see if two function curves are the same, we can subtract them and see which produces a horizontal flat line over the x axis.

Through trial-and-error, you should find that C(x) - G(x) will produce that flat line we're after.
It means C(x) - G(x) = 0 for all x in the domain, which leads to C(x) = G(x)

It's the same idea as saying something like 2+3 = 5, so 2+3-5 = 0.

---------------------------

Method 5

Use the route that tutor Edwin took.
It's a useful strategy for exams involving multiple choice (when in a time crunch and/or when completely stumped).
x = 0 is a common easy value to work with. It leads to 6^(4x+3) = 216 and k = 6.
You can then plug that k value into each answer choice to see which gives you 216.
If you had more than one answer choice produce 216, then pick something else for x.

Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!

Here's what to do in an EMERGENCY, but only in an EMERGENCY, and only on a multiple-choice test where you don't have to show your work. If you run into a problem like this on a multiple-choice test and don't know what to do, and are completely stuck, then here is a trick that works a lot of the time. Some other tutors here will frown on me for telling you this, but it works sometimes on certain problems. Substitute x=0. Then 6^(2*0+1) = 6 = k, then 6^(4*0+3) = 6^3 = 216 Then substitute 6 for k in every one of the choices: A) 12k = 12(6) = 72 That's not 216, so that eliminates A B) k^2 + 6 = (6)^2 + 6 = 42 That's not 216, so that eliminates B C) 6k^2 = 6(6)^2 = 6(36) = 216 That IS 216, but that only means it's POSSIBLY the right choice. For it happens sometimes that one of the others will also be 216. D) 2k + 6 = 2(6) + 6 = 18. That's not 216, so that eliminates D E) 36k^2 = 36(6)^2 = 1296 That's not 216, so that eliminates E So we know the correct choice is C. If another one of them had also come out 216, then you could do it again by substituting x=1 or x=-1. But if you're short on time, you still have a better chance of guessing correctly. Also sometimes, on some problems, substituting 0 in what's given and then in all the choices is the easiest method! Sometimes you can do it in your head! I have actually used it myself to save time even though I knew how to get the solution the regular way! As I mentioned above, sometimes substituting 1 or -1 is better than 0. Sometimes substituting 0 causes a denominator to be 0. Other times other numbers work better. So you can improvise on this method. But I'd better warn you, you'd better not rely on this method! It won't save you if you don't understand the material! Edwin

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
If 6^(2x+1) = k, then 6^(4x+3) equals
A 12k
B k^2 + 6
C 6k^2
D 2k + 6
E 36k^2
~~~~~~~~~~~~~~~~~~~~

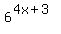= trace/watch attentively each and every my step = = 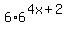= = 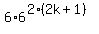= 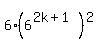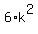. ANSWER. Option (C).

Solved.

Is everything clear to you from my solution ?

--------------------

In this problem, we have a given basic equation 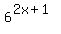   = k   and an expression to evaluate   .

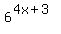An idea of the method is to transform the given "expression to evaluate" step by step to get the given basic expression
in it somewhere on the way, and then to replace one side of the given basic expression by its other side.

Then a miracle will happen literally in front of your eyes and you will get the required proof
(or evaluation, or reduction) in minutes ( ! )

If you will solve such problem once in your life (or if somebody will show you this trick
once in your life, as I do it here for you), you will MEMORIZE it and will be able to repeat it
in hundreds other similar problems/cases in your life.

It is worth to memorize HOW it works - then you will have a wonderful mathematical weapon in your possessions ( ! )

In his post, tutor @math_tutor2020 repeated my solution practically with no change - thanks to him for it,
even although he did not mention about it. Probably, he forgot to mention, or couldn't find the right/appropriate words.

---------------------

Dear tutor @math_tutor2020, when I tell about mentioning, I worry not about my rights.
I worry about a reader / (a student): what he will think by seeing
two identical texts in one post ? - At least, he will have mess in his/her mind.

It is what I'd like to avoid.

Question 1204836: If 6^(2x+1)=k , then 6^(4x+3) equals:
A) 12k
B) k^2 + 6
C) 6k^2
D) 2k+6
E) 36k^2
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
if 6^(2x+1) =k, then 6^(4x+3) equals
~~~~~~~~~~~~~

= trace/watch attentively each and every my step = = = = = . ANSWER. If 6^(2x+1) =k, then 6^(4x+3) equals .

Solved.

Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!

This was already done. Paste this in your browser: http://www.algebra.com/tutors/students/your-answer.mpl?question=1204752 Edwin

Question 1204808: if 6^(2x+1) =k, then 6^(4x+3 ) equals
Found 3 solutions by greenestamps, ikleyn, Edwin McCravy:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

Observe that 4k+3 = 2(2k+1)+1. Then

= = = =

ANSWER:

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.
if 6^(2x+1) =k, then 6^(4x+3) equals
~~~~~~~~~~~~~

= trace/watch attentively each and every my step = = = = = . ANSWER. If 6^(2x+1) =k, then 6^(4x+3) equals .

Solved.

Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!

This was already done http://www.algebra.com/tutors/students/your-answer.mpl?question=1204752 Edwin

Question 1204549: a uranium atom has a mass of 3.95 x 10^-22 grams. A sample of uranium has a mass of 9.085 x 10^-1 grams. Determine how many atoms are in the sample using scientific notation
please help I have a math test tomorrow
Found 2 solutions by josgarithmetic, math_tutor2020:
Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!
Number of atoms per gram

Sample of grams uranium

2.30*10^21 atoms

The given information limits to number to three significant figures.

Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

For the sake of a simple example, let's say that one single atom of uranium has a mass of 2 grams.
Of course this is way too large but it's for illustrative purposes only.

If we had a sample of 12 grams of uranium total, then we'd have 12/2 = 6 atoms.

Or in terms of algebra
2n = 12
n = 12/2
n = 6

-------------------------------------

Let's return back to real-world figures now.

We'll have n still represent the number of atoms.

We multiply this value n with the mass of one atom of uranium.
The expression (3.95x10^(-22))*n represents the total amount of mass, when we have n atoms of uranium.
The x refers to multiplication and it's not a variable.

Set this equal to the stated total amount 9.085x10^(-1) and let's isolate n.
(3.95x10^(-22))*n = 9.085x10^(-1)
n = 9.085x10^(-1) divide (3.95x10^(-22))
n = (9.085/3.95) x 10^(-1 - (-22) )
n = 2.3 x 10^21

This number is really massive. We write 23 and then have 20 zeros after the number.
The massive number is: n = 2,300,000,000,000,000,000,000
I started with 2.3 and then moved the decimal point 21 spots to the right to arrive at the large number shown above.

Scientific notation is best suited for massive numbers like this.

Answer: 2.3 x 10^21 atoms

Question 1204458: A uranium atom has a mass of 3.95× 10^−22 grams. A sample of uranium
has a mass of 9.085×10^−1 grams. Determine how many atoms are in
the sample using scientific notation?
Ⓐ 2.3× 10^−23
Ⓑ 2.3 × 10^21
Ⓒ 3.6 × 10^−22
Ⓓ 3.6 × 10^20
Found 2 solutions by mananth, Alan3354:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!
(9.085*10^(−1))/ (3.95* 10^(−22))
9.085/3.95)*(10^22/10^1)

2.303797*10^21

Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website!
A uranium atom has a mass of 3.95× 10^−22 grams. A sample of uranium
has a mass of 9.085×10^−1 grams. Determine how many atoms are in
the sample using scientific notation?
--------------------
n = 9.085e-1/3.95e-22 = (9.085/3.95)e21
= 2.3e21 or 2.3*10^21
-------------
= 2,300,000,000,000,000,000,000 atoms

Question 1204295: What can you say about the functions graphed below? Explain your reasoning: Is it a log or an exponential? For an exponential, is the exponent x or -x? What is the equation for the asymptote? Which direction and how many units is it shifted?
Graph A) https://app.gemoo.com/share/image-annotation/572889363786969088?codeId=Ml2kEYAjRgoXb&origin=imageurlgenerator
Graph B) https://app.gemoo.com/share/image-annotation/572889769845932032?codeId=v6gK8ZKQR0YZa&origin=imageurlgenerator
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Graph A represents a log function.

This particular curve passes through (3,3) and (12,6).

Consider the log equation template
y = a + b*log(x)
If we plugged in x = 1, then we get y = a.
This is because log(1) = 0 regardless of the base.

Unfortunately x = 1 isn't defined on your log graph.
But let's shift (3,3) and (12,6) two units to the left so that x = 1 would be defined.

(3,3) moves to (1,3)
(12,6) moves to (10,6)

If we plugged the coordinates of (1,3) into y = a+b*log(x), then we'd find that a = 3.

So y = a+b*log(x) updates to y = 3+b*log(x)

Now try the coordinates of (10,6) to determine b.
y = 3+b*log(x)
6 = 3+b*log(10)
6 = 3+b*1 ...... I'm using log base 10
6 = 3+b
b = 6-3
b = 3

We have y = 3 + b*log(x) update to y = 3 + 3*log(x)

This would be the answer if (1,3) and (10,6) were points on the curve.
However, recall we shifted things over 2 units to the left.
Shift 2 units to the right to undo that previous shift.

This means we'll replace x with x-2 to apply this shift we need.

The function that represents graph A is y = 3 + 3*log(x-2) where the log is base 10.

The vertical asymptote is x = 2 because this x value makes the stuff inside the log, the x-2 portion, equal to zero.
Recall that log(x) has the domain x > 0

Therefore the domain of y = 3 + 3*log(x-2) is x > 2.

The curve looks like it touches x = 2, but it never actually gets there. Think of it like an electric fence.

-------------------------------------------------------------------------------------------------------------------------

Now onto graph B. It appears this curve goes through (1,8) and (3,2).

This is an exponential decay curve.
This is due to the fact it decreases as we move to the right.
A real world example would be a half-life function.
The exponent is -x to indicate this decay.

The horizontal asymptote of the function y = a*b^(-x) is y = 0.

This curve shows the horizontal asymptote is y = 1.

Let's shift everything down by 1 so the horizontal asymptote y = 1 overlaps with the x axis (aka y = 0).

(1,8) moves to (1,7)
(3,2) moves to (3,1)

Let's look at the template
y = a*b^(-x)

To make the b term go away, we would plug in x = 0. But it's not clear what x = 0 leads to based on the graph you've provided (even after the vertical shift downward).

Let's move those points over 1 spot to the left.
(1,7) moves to (0,7)
(3,1) moves to (2,1)

Plug in the coordinates of (0,7) to find y = a*b^(-x) leads to a = 7.
So we now have y = 7*b^(-x)

Plug in (2,1) and solve for b
y = 7*b^(-x)
1 = 7*b^(-2)
1 = 7/(b^2)
1*b^2 = 7
b^2 = 7
b = sqrt(7)
b = 7^(1/2)
b = 7^(0.5)

So,
y = 7*b^(-x)
y = 7*(7^(0.5))^(-x)
y = 7*7^(-0.5x)

Next we'll shift 1 unit up and 1 unit right to undo those previous two shifts we did earlier.
y = 7*7^(-0.5x)
becomes
y = 7*7^(-0.5(x-1))+1
I'll let you simplify if needed.

There is probably a much more elegant, clever, and efficient way to determine this function.
I'll let another tutor provide that route. Feel free to explore other methods.

I recommend using a tool like GeoGebra or Desmos to confirm we have the correct functions.

Here is a link to the interactive Desmos graph
https://www.desmos.com/calculator/wc4mvapjx7

Question 1204273: 3 to the -7th power times 2 to the -4th power
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website!
(1/2187)((1/16)=1/34992=2.8578*10^(-5)
or by logs
-7 log3+-4log2=-4.54397
raise 10 to that power=0.000028578 or 2.8578 x 10^(-5)

Question 1203032: Determine the value of k such that the trinomial 4x^2-kx+81 is a perfect square (such as (ax+b)^2.
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.

We write 4x^2 - kx + 81 = . It gives us 4x^2 - kx + 81 = a^2*x^2 + 2abx + b^2. From this, we conclude that either (a) a = 2, b = 9, or (b) a = -2, b = 9, or (c) a = 2, b = -9 or (d) a = -2, b = -9. It gives for "k" two and only two opportunities: either k = 2ab = 36 or k = 2ab = -36.

Solved.

/////////////////////

Be attentive: the problem INCORRECTLY asks about "the value of k",
while a correct question must be "find all possible values of k".

So, the problem's formulation has a huge underwater stone (is a trap),
expecting you will fall in it.

Question 1053349: Prove That:
(tan^2 A + 1)Cos2A= 2-Sec^2A
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!

(tan^2 A + 1)Cos2A= 2-Sec^2A

(tan^2A+1)(cos^2A-sin^2A)

sec^2A *(cos^2A-(1-cos^2A)

sec^2A *(cos^2A-1+cos^2A)

1/cos^2A *2cos^2A -1/cos^2A

=2-sec^2A