Question 1175054: Assume there is a certain population of fish in a pond whose growth is described by the logistic equation. It is estimated that the carrying capacity for the pond is 1500 fish. Absent constraints, the population would grow by 200% a year.
If the population is given by po=600, then after one breeding season the population of the pond is given by
p1=
After two breeding seasons the population of the pond is given by
p2=
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if the growth is 200% per year, then the growth rate is 2 per year.
the formula for future value is f = p * (1 + r) ^ n
f is the future value
p is the present value
r is the rat4e of growth per year.
n is the number of years.
in your problem, the formula becomes f = 600 * (1 + 2) ^ n
p1 is the number at the end of 1 year.
p2 is the number at the end of 2 years.
p1 = 600 * 3^1 = 1800
p2 = 600 * 3^2 = 5400
how does this work?
the population is 600 in p0.
the growth is 200% per year, meaning the growth is 1200 from p0 to p1.
the population is 600 + 1200 = 1800 in p1.
the growth is 200% per year, meaning the growth is 3600 from p1 to p2.
the population is 1800 + 3600 = 5400 in p2.
since the carrying capacity of the pond is 1500 fish, it's pretty clear that there's not a lot of room for growth.
at the given growth rate of 200% per year, the pond is over capacity at the end of 1 year.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Assume there is a certain population of fish in a pond whose growth is described
by the logistic equation. It is estimated that the carrying capacity for the pond is 1500 fish.
Absent constraints, the population would grow by 200% a year.
If the initial population is given by po= 600, then estimate the fish population in the pond
after one and two years
~~~~~~~~~~~~~~~~~~~~~~~~~~~
One good Internet source for a beginner to read and to learn about a logistic equation is Libre text
https://math.libretexts.org/Bookshelves/Calculus/Calculus_(OpenStax)/08%3A_Introduction_to_Differential_Equations/8.04%3A_The_Logistic_Equation
This my post is to overlay calculations by the other tutor, that are irrelevant.
The general solution for the standard logistic differential equation is so called logistic function
P(t) = 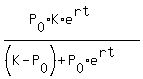 .
Here .
Here 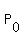 is the initial population, P(t) is current population, K is the carrying capacity
and "r" is growth rate. Number "e" = 2.71828 is the base of natural logarithm
(shown here as an approximate value).
In this current problem in the post, we are given is the initial population, P(t) is current population, K is the carrying capacity
and "r" is growth rate. Number "e" = 2.71828 is the base of natural logarithm
(shown here as an approximate value).
In this current problem in the post, we are given
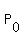 = 600, K = 1500, r = 2.0.
They want you determine P(1) and P(2), the population after 1 and 2 years.
(a) For t = 1 year
P(1) = = 600, K = 1500, r = 2.0.
They want you determine P(1) and P(2), the population after 1 and 2 years.
(a) For t = 1 year
P(1) = 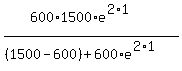 = 1246.879478, or 1247 (rounded).
(b) For t = 2 years
P(2) = = 1246.879478, or 1247 (rounded).
(b) For t = 2 years
P(2) = 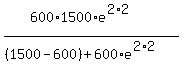 = 1459.89162, or 1460 (rounded). = 1459.89162, or 1460 (rounded).
Solved.
-------------------
Post-solution notice
In my opinion, the question in the post is posed/worded INCORRECTLY.
It asks about the breeding season, but we are not given information
for a breeding season - we are given information, related to years - so,
the question should be about the times of years, not the breeding seasons.
The life of fish includes not only breeding - it includes also struggle for food,
survival from predators and diseases, natural death, that is, processes with a period of a year.
|
|
|