Tutors Answer Your Questions about Exponents-negative-and-fractional (FREE)
Question 1209817: Let
P = 3^{1/3} \cdot 9^{1/9} \cdot 27^{1/27} \cdot 81^{1/81}.
Then P can be expressed in the form \sqrt[a]{b}, where $a$ and $b$ are positive integers. Find the smallest possible value of $a + b.$
Found 3 solutions by ikleyn, Edwin McCravy, CPhill:
Answer by ikleyn(52873)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
@CPhill writes in his post
8. **Calculate 3^58:**
* 3^58 = 4710128697246244834921603770
It is totally wrong.
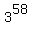 can not end by the "0" digit. can not end by the "0" digit.
Last digit of 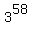 is 9. is 9.
So, the answer in the post by @CPhill is INCORRECT.
Answer by Edwin McCravy(20063)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There's that notation again that I have not completely figured out which is
not compatible with the HTML this site is written in. Maybe this the correct
interpretation. [If this was posted by a human, I would appreciate it if you
post again, to use standard notation.]
 a=81, b=358.
So the smallest possible value of 81+358 = 4710128697246244834921603770
Edwin
a=81, b=358.
So the smallest possible value of 81+358 = 4710128697246244834921603770
Edwin
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down the problem step by step:
1. **Express all terms with the same base:**
* P = 3^(1/3) * (3^2)^(1/9) * (3^3)^(1/27) * (3^4)^(1/81)
* P = 3^(1/3) * 3^(2/9) * 3^(3/27) * 3^(4/81)
2. **Combine the exponents:**
* P = 3^(1/3 + 2/9 + 3/27 + 4/81)
3. **Find a common denominator:**
* The least common denominator is 81.
* P = 3^(27/81 + 18/81 + 9/81 + 4/81)
4. **Add the fractions:**
* P = 3^(58/81)
5. **Express in radical form:**
* P = (3^58)^(1/81)
* P = ⁸¹√(3^58)
6. **Identify a and b:**
* a = 81
* b = 3^58
7. **Calculate a + b:**
* a + b = 81 + 3^58
8. **Calculate 3^58:**
* 3^58 = 4710128697246244834921603770
9. **Calculate a+b**
* a + b = 81 + 4710128697246244834921603770 = 47101286972462448349216037751
Therefore, the smallest possible value of a + b is 81 + 3^58.
Question 1209816: Let
P = 2^{1/2} \cdot 4^{1/4} \cdot 8^{1/8} \cdot 16^{1/16}
Then P can be expressed in the form \sqrt[a]{b}, where $a$ and $b$ are positive integers. Find the smallest possible value of $a + b.$
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's rewrite the expression for $P$ using powers of 2:
$$P = 2^{1/2} \cdot (2^2)^{1/4} \cdot (2^3)^{1/8} \cdot (2^4)^{1/16}$$
$$P = 2^{1/2} \cdot 2^{2/4} \cdot 2^{3/8} \cdot 2^{4/16}$$
$$P = 2^{1/2} \cdot 2^{1/2} \cdot 2^{3/8} \cdot 2^{1/4}$$
Now, let's add the exponents:
$$P = 2^{1/2 + 1/2 + 3/8 + 1/4} = 2^{1 + 3/8 + 2/8} = 2^{1 + 5/8} = 2^{13/8}$$
We want to express $P$ in the form $\sqrt[a]{b}$, which means $P = b^{1/a}$.
So we have $P = 2^{13/8} = (2^{13})^{1/8}$.
Thus, we can write $P = \sqrt[8]{2^{13}}$.
In this case, $a = 8$ and $b = 2^{13} = 8192$.
Then $a + b = 8 + 8192 = 8200$.
We want to find the smallest possible value of $a + b$.
Let $P = 2^{13/8}$. We can write this as $P = (2^{13k})^{1/(8k)}$ for any positive integer $k$.
When $k=1$, $a=8$ and $b=2^{13} = 8192$, so $a+b = 8200$.
When $k=2$, $a=16$ and $b=2^{26}$, so $a+b = 16 + 2^{26} = 16 + 67108864 = 67108880$.
Since $2^{13/8}$ is already in its simplest form, we cannot reduce the fraction 13/8 further. So the smallest possible value for $a$ is 8.
Thus, the smallest possible value of $a + b$ is $8 + 2^{13} = 8 + 8192 = 8200$.
Final Answer: The final answer is $\boxed{8200}$
Question 1200305: Let’s say you are remodeling your room. You want to determine various measurements using
polynomial expressions. Your room is
8x
feet by
3x
feet.
1. How much border should you purchase is you are putting border around the edge of the top of
your walls? (Assume there is wall space above the opening for the door).
2. On the floor, you will need to purchase wood floor panels. How much should you buy to
cover the entire floor of your bedroom?
3. Your mom just told you that she will give you your sister’s bedroom which as 3 more feet of
length and 2 less feet of width. What is the new amount of border you will need to purchase?
4. In the new room, what is the new amount of flooring you will need to purchase?
5. What is the difference in the size of the new bedroom and the original bedroom?
Answer by GingerAle(43)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, let's figure out the measurements for your room remodel!
**1. Border for the top of the walls:**
* **Find the perimeter:**
* Perimeter = 2 * (Length + Width)
* Perimeter = 2 * (8x + 3x) = 2 * 11x = 22x feet
* **You should purchase 22x feet of border.**
**2. Flooring for the original room:**
* **Find the area:**
* Area = Length * Width
* Area = 8x * 3x = 24x² square feet
* **You should purchase 24x² square feet of flooring.**
**3. Border for the new room:**
* **New room dimensions:**
* Length = 8x + 3 = (8x + 3) feet
* Width = 3x - 2 = (3x - 2) feet
* **Find the new perimeter:**
* Perimeter = 2 * (Length + Width)
* Perimeter = 2 * [(8x + 3) + (3x - 2)] = 2 * (11x + 1) = 22x + 2 feet
* **You should purchase 22x + 2 feet of border for the new room.**
**4. Flooring for the new room:**
* **Find the new area:**
* Area = Length * Width
* Area = (8x + 3) * (3x - 2)
* Area = 24x² - 16x + 9x - 6
* Area = 24x² - 7x - 6 square feet
* **You should purchase 24x² - 7x - 6 square feet of flooring for the new room.**
**5. Difference in size between the new and original bedrooms:**
* **Find the difference in area:**
* Difference = New Room Area - Original Room Area
* Difference = (24x² - 7x - 6) - 24x²
* Difference = -7x - 6 square feet
* **The new bedroom is 7x + 6 square feet smaller than the original bedroom.**
I hope this helps! Let me know if you have any other questions.
Question 1209202: To solve for -6(-2+n)=102, I know -6x-2=12, but when I solve for -6 times positive n would the equation then be -6n+12 or 12-6n?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
-6n+12 is the same as 12 + (-6n) or simply 12-6n
Think of the template a+b = b+a which says we can add two numbers in any order.
In this case a = -6n and b = 12.
To solve -6(-2+n) = 102, you could distribute to get 12-6n = 102
Or
You could divide both sides by -6 to get -2+n = -17
I'll let the student finish up.
Answer by ikleyn(52873)   (Show Source): (Show Source):
Question 1208146: Simplify each expression. Express the answer so that all exponents are positive. Whenever an exponent is 0 or negative, we assume that the base is NOT 0.
1. [(4x^(-2)(yz)^(-1)]/[(2^3)(x^4)y]
2. [(5x^(-2))/(6y^(-2)]^(-3)
Answer by josgarithmetic(39629)  (Show Source): (Show Source):
Question 1175054: Assume there is a certain population of fish in a pond whose growth is described by the logistic equation. It is estimated that the carrying capacity for the pond is 1500 fish. Absent constraints, the population would grow by 200% a year.
If the population is given by po=600, then after one breeding season the population of the pond is given by
p1=
After two breeding seasons the population of the pond is given by
p2=
Answer by ikleyn(52873)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Assume there is a certain population of fish in a pond whose growth is described
by the logistic equation. It is estimated that the carrying capacity for the pond is 1500 fish.
Absent constraints, the population would grow by 200% a year.
If the initial population is given by po= 600, then estimate the fish population in the pond
after one and two years
~~~~~~~~~~~~~~~~~~~~~~~~~~~
One good Internet source for a beginner to read and to learn about a logistic equation is Libre text
https://math.libretexts.org/Bookshelves/Calculus/Calculus_(OpenStax)/08%3A_Introduction_to_Differential_Equations/8.04%3A_The_Logistic_Equation
This my post is to overlay calculations by the other tutor, that are irrelevant.
The general solution for the standard logistic differential equation is so called logistic function
P(t) = 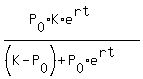 .
Here .
Here 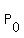 is the initial population, P(t) is current population, K is the carrying capacity
and "r" is growth rate. Number "e" = 2.71828 is the base of natural logarithm
(shown here as an approximate value).
In this current problem in the post, we are given is the initial population, P(t) is current population, K is the carrying capacity
and "r" is growth rate. Number "e" = 2.71828 is the base of natural logarithm
(shown here as an approximate value).
In this current problem in the post, we are given
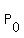 = 600, K = 1500, r = 2.0.
They want you determine P(1) and P(2), the population after 1 and 2 years.
(a) For t = 1 year
P(1) = = 600, K = 1500, r = 2.0.
They want you determine P(1) and P(2), the population after 1 and 2 years.
(a) For t = 1 year
P(1) = 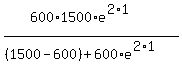 = 1246.879478, or 1247 (rounded).
(b) For t = 2 years
P(2) = = 1246.879478, or 1247 (rounded).
(b) For t = 2 years
P(2) = 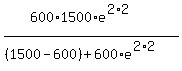 = 1459.89162, or 1460 (rounded). = 1459.89162, or 1460 (rounded).
Solved.
-------------------
Post-solution notice
In my opinion, the question in the post is posed/worded INCORRECTLY.
It asks about the breeding season, but we are not given information
for a breeding season - we are given information, related to years - so,
the question should be about the times of years, not the breeding seasons.
The life of fish includes not only breeding - it includes also struggle for food,
survival from predators and diseases, natural death, that is, processes with a period of a year.
Question 1206141: Assume there is a certain population of fish in a pond whose growth is described by the logistic equation. It is estimated that the carrying capacity for the pond is 1600 fish. Absent constraints, the population would grow by 120% per year.
If the starting population is given by ,p0=200 then after one breeding season the population of the pond is given by
P1=
after two breeding seasons the population of the pond is given by
P2=
Answer by ikleyn(52873)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Assume there is a certain population of fish in a pond whose growth is described by the logistic equation.
It is estimated that the carrying capacity for the pond is 1600 fish. Absent constraints,
the population would grow by 120% per year.
If the starting population is given by p0=200, then estimate population of fish in the pond
after one and two years.
~~~~~~~~~~~~~~~~~~~~~
One good Internet source to read and to learn about a logistic equation is Libre text
https://math.libretexts.org/Bookshelves/Calculus/Calculus_(OpenStax)/08%3A_Introduction_to_Differential_Equations/8.04%3A_The_Logistic_Equation
The general solution for the standard logistic differential equation is so called logistic function
P(t) = 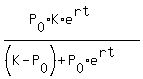 .
Here .
Here 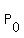 is the initial population, P(t) is current population, K is the carrying capacity
and "r" is growth rate. Number "e" = 2.71828 is the base of natural logarithm
(shown here as an approximate value).
In this current problem in the post, we are given is the initial population, P(t) is current population, K is the carrying capacity
and "r" is growth rate. Number "e" = 2.71828 is the base of natural logarithm
(shown here as an approximate value).
In this current problem in the post, we are given
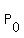 = 200, K = 1600, r = 1.2.
They want you determine P(1) and P(2), the population after 1 and 2 years.
(a) For t = 1 year
P(1) = = 200, K = 1600, r = 1.2.
They want you determine P(1) and P(2), the population after 1 and 2 years.
(a) For t = 1 year
P(1) =  = 514.74, or 514 (rounded).
(b) For t = 2 years
P(2) = = 514.74, or 514 (rounded).
(b) For t = 2 years
P(2) =  = 978.58, or 979 (rounded). = 978.58, or 979 (rounded).
Solved.
-------------------
Post-solution notice
In my opinion, the question in the post is posed/worded INCORRECTLY.
It asks about the breeding season, but we are not given information
for a breading season - we are given information, related to years - so,
the question should be about the times of years, not the breeding seasons.
The life of fish includes not only breeding - it includes also struggle for food,
survival from predators and diseases, natural death, that is, processes with a period of a year.
Question 1204152: +21y3negative 3 y to the fifth power minus 9 y to the fourth power plus 21 y cubed\(-3y^{5}-9y^{4}+21y^{3}\)
simplified
Found 2 solutions by ikleyn, mananth:
Answer by ikleyn(52873)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In Math, it is commonly accepted to write formulas using mathematical transcription
as a standard mathematical language, and is not accepted to re-tell the formulas using words.
When somebody tries to retell a Math formula using words, it is a sign of a common deep and total mathematical illiteracy.
Answer by mananth(16946)   (Show Source): (Show Source):
Question 1203449: 7(2x-4)-(10-3x)
Answer by mccravyedwin(408)   (Show Source): (Show Source):
Question 1202579: Use the properties of exponents to create an equivalent expression for the given expression
shown below with no variables in the denominator.
(64𝑥^2)^−1/6 * (32𝑥^5)^-2/5
Answer by mananth(16946)   (Show Source): (Show Source):
Question 1202091: why -2 to the power of 4 = -16?
Found 4 solutions by greenestamps, math_tutor2020, MathTherapy, ikleyn:
Answer by greenestamps(13208)   (Show Source): (Show Source):
You can put this solution on YOUR website!
When the expression is written in words, instead of with formal mathematical symbols, there are two different interpretations that give different answers.
(-2) to the power of 4 = (-2)^4 = 16
-(2 to the power of 4) = -(2^4) = -16
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
It's a matter of order of operations (PEMDAS)
If we write (-2)^4, then
(-2)^4 = (-2)*(-2)*(-2)*(-2) = 16
The (-2)^4 means "multiply four copies of (-2) together to get 16"
The four negatives pair up and cancel out
negative * negative = positive
If on the other hand we have -(2^4), then,
-(2)^4 = -(2)*(2)*(2)*(2) = -16
The key difference this time is the negative doesn't get copied four times
We evaluate 2^4 first, then stick a negative at the front, to end up with -16.
Recall that PEMDAS has us do the parenthesis part first, then multiplication later. Think of -(2^4) as -1*(2^4)
Side note: many calculators will interpret -2^4 as -(2^4) and not as (-2)^4
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
why -2 to the power of 4 = - 16?
- 24 = (- 2)4 is NOT equal to - 16
However, it CAN BE if it's written a certain way. Can you determine that way?
Answer by ikleyn(52873)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
why -2 to the power of 4 = -16?
~~~~~~~~~~~~~~~~
-2 to the power of 4 is not -16.
-2 to the power of 4 is 16.
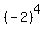 = (-2)*(-2)*(-2)*(-2) = 16. ANSWER = (-2)*(-2)*(-2)*(-2) = 16. ANSWER
Question 1201491: Assume there is a certain population of fish in a pond whose growth is described by the logistic equation. It is estimated that the carrying capacity for the pond is 1900 fish. Absent constraints, the population would grow by 210% per year.
If the starting population is given by p0=600
, then after one breeding season the population of the pond is given by
p1=
After two breeding seasons the population of the pond is given by
p2=
Answer by Glaviolette(140)   (Show Source): (Show Source):
Question 1201316: What is halfway between -2 and -5
Found 2 solutions by math_helper, ikleyn:
Answer by math_helper(2461)   (Show Source): (Show Source):
Answer by ikleyn(52873)   (Show Source): (Show Source):
Question 1199795: can you help me on this hehe i need 3 examples of every law of exponents(FIRST TO FOURTH LAW) thank you so much
The Product rule for radicals
root(xy, n) = root(x, n) * root(y, n)
where x and y are nonnegative numbers and n is a counting number.
The Quotient Rule for Radicals:
root(x/y, n) = (root(x, n)/(root(y, n)
where x and y are nonnegative numbers and y=0.
Additional Rule:
root(m) root(n) x = root(mn)x
Laws of Radicals
First Law of Exponents: xm. xn = xm+n
Second Law of Exponents: xm/xn = xm-n; if x = 0 and m>n
Third Law of Exponents: (xm)n = xmn
Fourth Law of Exponents: (xy)m = xmym
Extension of the Second Law of Exponents:
1. The Zero Exponent: x0 = 1; where x = 0.
2. Definition of Negative Exponent: x-n= 1/xn where x = 0 and n is a counting number.
Answer by Solver92311(821)   (Show Source): (Show Source):
Question 1199813: what is 1/8 to the power of 4
Answer by josgarithmetic(39629)  (Show Source): (Show Source):
Question 1199265: Solve for x.
2x^(2/3) - 5x^(1/3) - 3 = 0
Using the Diamond Method, I got the following:
2x^(2/3) - 6x^(1/3) + x^(1/3) - 3 = 0
I then applied factoring by group.
2x^(1/3)[x^(1/3) - 3]
Setting each factor to 0 and solving for x, I got the following
values: 0, 27
According to the textbook, x = 27 is one of the solutions.
The second value of x should be -1/8.
I did everything I could think of to find the second value of x but to no avail.
How do I find x = -1/8?
Answer by ikleyn(52873)   (Show Source): (Show Source):
Question 1197601: The half life of a certain isotope is 8.5. If we we have a sample of 10 ounces of isotope show much of it will remain after one full day. One of 4 choices is the answer. 0.28 ounces, 0
14 ounces, 1.41 ounces, or 2.83 ounces. Which answer is correct?
Found 4 solutions by ewatrrr, greenestamps, ikleyn, josgarithmetic:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
Answer by greenestamps(13208)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Obviously the post is made carelessly, without a time unit on the half life. But given the answer choices, we can determine logically what those units are.
We start with 10 ounces, and the answer choices for the amounts remaining after 1 day (24 hours) are between 0.28 and 2.83 ounces. Since the amount of the isotope decreases by 1/2 every half life, 24 hours has to be approximately 3 to 4 half lives; that means the given half life of "8.5" is in fact 8.5 hours.
So the number of half lives is 24/8.5, and the amount remaining after 24 hours is, to 2 decimal places, is

Answer by ikleyn(52873)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Without pointing half-life dimension (year, day, hour, minute etc.) this problem MAKES no SENSE,
and the question can not be answered properly.
Answer by josgarithmetic(39629)  (Show Source): (Show Source):
You can put this solution on YOUR website! Half life of 8.5, what? Time unit needed. Either days or hours most likely
8.5 HOURS, the half life.
1.41 ounces after 24 hours.
Question 1197001: 2 to the power of -5 =
Answer by Theo(13342)   (Show Source): (Show Source):
Question 1196955: Which number has the greatest value?
-4
-3 1/2
-5 1/2
-4 1/2
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1196410: The most common roach in the United States is the German cockroach. In a
year, a home can be infested with about 30,000 cockroaches. About how many
cockroaches would infest a home in one month?
a 2.5 × 10^3
b 2.5 × 10^4
c 3.6 × 10^4
d 3.6 × 10^5
Found 2 solutions by MathTherapy, ikleyn:
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The most common roach in the United States is the German cockroach. In a
year, a home can be infested with about 30,000 cockroaches. About how many
cockroaches would infest a home in one month?
a 2.5 × 10^3
b 2.5 × 10^4
c 3.6 × 10^4
d 3.6 × 10^5
Number in a year: 30,000
Number in a month: 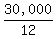 Looking at the answers, you now need to convert
Looking at the answers, you now need to convert 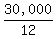 into SCIENTIFIC NOTATION form. into SCIENTIFIC NOTATION form.
Answer by ikleyn(52873)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To answer this question, an appropriate mathematical model is needed.
Without an adequate model, your question makes no sense.
What I want to say is that an exponential growth model will give different answer than a linear model.
Since the model is not specified in the post, the question makes no sense.
Question 1195505: A box contains 5 white and 4 blue marbles. Two marbles are drawn from the box in succession without replacement. What is the probability of getting a white on the second draw given that it is white on the first draw?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
"given that it is white on the first draw" is important phrasing. We know 100% that the first marble is white.
Since the marble isn't replaced, we drop to 5-1 = 4 white marbles remaining out of 5+4-1 = 8 total marbles left.
The probability of getting another white marble is 4/8 = 1/2
Answer: 1/2
Answer by ikleyn(52873)   (Show Source): (Show Source):
Question 1191665: Determine a function, I(t), that determines Jennifer’s investment account balance after t
years. For the exponential growth function, what are the “a” and “b” values? What do those values represent? (5 points for the explanation of “a” and “b” and 5 points for the function)
2. Calculate how much money Jennifer will have after 10 years. (10 points)
3. What is Jennifer was able to deposit $100,000 as her initial investment, instead of $50,000.
Write a new function, N(t), to show this change. (3 points) Calculate how much money Jennifer would have after 8 years. (2 points)
Using complete sentences, compare the differences in the functions and the amount of money after 8 years for the two different functions. (5 points)
University of Texas at Austin UT High School 1
4. Graph the function I(t) and identify the y-intercept and the equation of the asymptote. (5 pts)
5. Graph the function N(t) and identify the y-intercept and the equation of the asymptote. (5 pts)
6. What does the asymptote mean in terms of Jennifer’s investment account? Be sure to explain your reasoning for credit. (5 pt)
7. Due to a worldwide recession, Jennifer’s financial advisor informs her the account is no longer growing after 4 years. He recommends she move her money to an account that is more conservative and earns only 4% annually. Determine the amount in Jennifer’s investment account after 4 years(using the $50,000 investment), rounding to the nearest dollar. It may be helpful to create a table. (10 points)
8. Write a new function, N(t), that represents the amount of money in Jennifer’s new account after t years. Be sure to use correct notation. (5 pts)
9. Did the asymptote of the new function change due to Jennifer moving her investment? Explain your reasoning. (5 pts)
Answer by ikleyn(52873)   (Show Source): (Show Source):
Question 1187099: (8/7)^-2 Rewrite the following without an exponent.
Answer by Alan3354(69443)   (Show Source): (Show Source):
Question 1185915:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Question 1185916: (-3) to the -2 power
Answer by Alan3354(69443)   (Show Source): (Show Source):
Question 1184034: If x is not equal to 0, then
x-2y/2y-x + 2y-x/x-2y
The correct answer is -2 but I don't know how that the answer.
Found 2 solutions by greenestamps, Theo:
Answer by greenestamps(13208)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Curiously, the expression you show is indeed equal to -2; and the expression you undoubtedly INTENDED to show is also equal to -2.
Here is the expression you show: "x-2y/2y-x + 2y-x/x-2y"

Here, on the other hand, is the expression you most probably meant: "(x-2y)/(2y-x)+(2y-x)/(x-2y)"

If you are working problems like this, your math knowledge should be great enough to know that proper use of parentheses is important...!
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! it looks like the correct answer really is -2.
the expression is:
(x-2y) / (2y-x) + (2y-x) / (x-2y)
(x-2y) is equal to -1 * (2y-x)
(2y-x) is equal to -1 * (x-2y)
the expression becomes:
-(2y-x)/(2y-x) + -(x-2y)/(x-2y) which is equal to:
-1 + -1 which is equal to:
-2
Question 1183428: Assume there is a certain population of fish in a pond whose growth is described by the logistic equation. It is estimated that the carrying capacity for the pond is 2000 fish. Absent constraints, the population would grow by 210% per year.
If the starting population is given by p0=500, then after one breeding season the population of the pond is given by
p1 =
After two breeding seasons the population of the pond is given by
p2 =
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Logistic equation is y=L/(1+be^(-kt)) and dP/dT=kP(1- (P/L))
L=2000, the carrying capacity.
k=constant of proportionality, or 2.1
Using the first,
t=0; 500=2000/(1+be^0)
500(1+b)=2000
b=3
t=1 season
y(1)=2000/(1+3e^(-2.1)=1462.66 or 1463
y(2)=2000/(1+3e^(-4.2))=1913.90 or 1914

Question 1183330: The container that holds the water for the football team is 1/2 full. After pouring out 5 gallons of water, it is 3/10 full. How many gallons can the container hold?
Answer by josgarithmetic(39629)  (Show Source): (Show Source):
You can put this solution on YOUR website! From 1/2 full to 3/10 full is 5 gallons.
From 5/10 full to 3/10 full is 5 gallons.
2/10 of container is 5 gallons.
1/5 of the container is 5 gallons.
Make your reasoning from  of the container is 5 gallons. of the container is 5 gallons.
Question 1183275: If 800g of a radioactive substance are present initially and 8 years later only 450g remain, how much of the substance will be present after 16 years?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52873)   (Show Source): (Show Source):
Answer by greenestamps(13208)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Over the space of 8 years, the amount remaining decreases by a factor of 450/800 = 9/16.
After another 8 years, the amount will again decrease by the same factor.
ANSWER: (9/16)*450 = 253 1/8
Since radioactive decay is a statistical process, it should be okay to round the answer to 253g.
Question 1180899: Given that :3x power 4 *(2x) power 3 over 12x power-2 =Ax power n where A and n are integers. Find the value of A and n.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330
|







