Question 1199250: The half-life of a radioactive substance is one hundred twenty-five days. How many days will it take for eighty-two percent of the substance to decay?
A. 180
B. 367
C. 275
D. 310
E. 532
F. 426
Found 5 solutions by Theo, Edwin McCravy, ikleyn, greenestamps, MathTherapy:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! half life is 125 days.
formula becomes .5 = g ^ 125
g is the growth rate per day.
take the 125th root of both sides of the equation to get:
.5 ^ (1/125) = g
solve for g to get:
g = .9944701687
that's the daily growth rate.
if the radioactive substance starts at 1 and you want 82% to decay, then the remainder would be 1 - .82 * 1 = .18.
the formula decays from 1 to .18 in x days.
the formula becomes .18 = 1 * .9944701687 ^ x
simplify to get .18 = .9944701687 ^ x
take the log of both sides of the equation to get:
log(.18) = log(.9944701687 ^ x)
this becomes log(.18) = x * log(.9944701687)
solve for x to get:
x = log(.18) / log(.9944701687) = 309.2413985 days.
that's pretty close to 310, so selection D should be your answer.
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The formula is
 , where Ao is the beginning amount, A is the final amount,
t is time required to reach the final amount, and k is a constant.
If we start with quantity P, then when t = 25, the final amount A is half
the starting amount P, so , where Ao is the beginning amount, A is the final amount,
t is time required to reach the final amount, and k is a constant.
If we start with quantity P, then when t = 25, the final amount A is half
the starting amount P, so  . .
 Cancel the P's
Cancel the P's

 Take natural logs of both sides:
Take natural logs of both sides:



 Now we go back to
Now we go back to
 and replace k by -0.0055451774
and replace k by -0.0055451774
 Now we must find how many days it will take for eighty-two percent
of the substance to decay?
Remember, A is how much is left, not how much decaying has been
done, so when 82% of the stuff decays, what's left is 100%-82% = 18%.
So we substitute 0.18P for A
Now we must find how many days it will take for eighty-two percent
of the substance to decay?
Remember, A is how much is left, not how much decaying has been
done, so when 82% of the stuff decays, what's left is 100%-82% = 18%.
So we substitute 0.18P for A
 Cancel P's
Cancel P's





 Not quite all 82% will have decayed on the 309th day,
but it will all will be decayed on the 310th day.
Edwin
Not quite all 82% will have decayed on the 309th day,
but it will all will be decayed on the 310th day.
Edwin
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The half-life of a radioactive substance is one hundred twenty-five days. How many days will it take for eighty-two percent of the substance to decay?
A. 180
B. 367
C. 275
D. 310
E. 532
F. 426
~~~~~~~~~~~~~~~~~
The half-life is given, so I write the exponential decay function
in the base  in terms of half-lives (in a way as it in terms of half-lives (in a way as it  be done based on given info)
m(t) = be done based on given info)
m(t) = 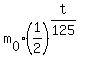 , (1)
where m(t) is the current remaining mass, , (1)
where m(t) is the current remaining mass, 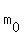 is the starting mass and t is the time, in days.
We are given that m(t) = is the starting mass and t is the time, in days.
We are given that m(t) = 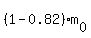 = =  , so , so 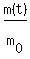 = 0.18.
Therefore, equation (1) takes the form = 0.18.
Therefore, equation (1) takes the form
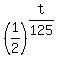 = 0.18.
We want to find "t" from this equation. For it, transform it step by step.
First step is to take logarithm base 10 of both sides = 0.18.
We want to find "t" from this equation. For it, transform it step by step.
First step is to take logarithm base 10 of both sides
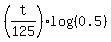 = log(0.18)
From it, express t and calculate
t = = log(0.18)
From it, express t and calculate
t = 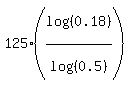 = 309.24 days.
309.24 days is the required "continuous" time (real value).
If you want to get the answer as an integer number of days with a necessary margin,
round it to the closest greater integer number, which is 310. = 309.24 days.
309.24 days is the required "continuous" time (real value).
If you want to get the answer as an integer number of days with a necessary margin,
round it to the closest greater integer number, which is 310.
Solved.
-----------------
Post-solution note :
when the half-life is given, write the exponential decay function in terms of half-life
with the base  . It is the commonly accepted traditional GOOD STYLE. . It is the commonly accepted traditional GOOD STYLE.
Writing in other form (ekt-form), as Edwin makes it, IS NOT a good style when half-life is given.
Writing equation in the right form is not only the choice of the style.
Doing this way as I did, you perform only those calculations,
that are REALLY necessary, and do not make UNNECESSARY calculations.
It is the major reason of choosing that or the other style/approach.
///////////////
On radioactive decay, see the lesson
- Radioactive decay problems
in this site.
You will find many similar (and different) solved problems there.
Use this lesson as your handbook, textbook, guide, tutorials, and (free of charge) home teacher.
Learn the subject from there once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|