|
Tutors Answer Your Questions about Evaluation Word Problems (FREE)
Question 1185401: Shreya is very interested in cryogenics (the science of very low temperatures). With the help of her science teacher she is doing an experiment on the effect of low temperatures on bacteria. She cools one sample of bacteria to a temperature of -51°C, another to -45oC, a third to -81oC, and finally another to -76°C. What was the temperature difference in the two coldest experiments? Each experiment began with 12 individual bacteria, and the strain of cold resistant bacteria she was testing stopped growing at -47oC, and they doubled each minute. Further, the bacteria started to die off at 75oC, losing ⅓ of the colony each minute. How many bacteria will Shreya have at the end of the third experiment if she began the experiment at 13oC, and it takes 15 seconds to increase or decrease the temperature by 1 degree?
Answer by CPhill(1987)   (Show Source):
You can put this solution on YOUR website! Here's how to break down this problem:
1. **Temperature Difference:** The two coldest temperatures are -81°C and -76°C. The difference between them is |-81 - (-76)| = |-81 + 76| = |-5| = 5°C.
2. **Bacteria Growth (Irrelevant to the question asked):** The information about the bacteria doubling and dying off, and the temperature at which they stop growing or start dying is extra information and not needed to answer the temperature difference question.
3. **Bacteria in the third experiment:**
* **Initial Temperature:** 13°C
* **Target Temperature:** -81°C
* **Temperature Difference:** 13 - (-81) = 94°C
* **Time to cool:** 94°C * 15 seconds/°C = 1410 seconds
* **Minutes to cool:** 1410 seconds / 60 seconds/minute = 23.5 minutes
Since the bacteria stop growing at -47°C, we need to determine how long it takes to reach that temperature:
* Temperature difference to reach -47°C: 13 - (-47) = 60°C
* Time to reach -47°C: 60°C * 15 seconds/°C = 900 seconds = 15 minutes.
For the first 15 minutes, the bacteria doubles every minute. So, after 15 minutes, the number of bacteria will be 12 * 2^15 = 393216.
The bacteria stops growing at -47°C. The experiment cools to -81°C, which is much lower, so the bacteria will not grow beyond that point. The time to reach -81°C is 23.5 minutes, but the bacteria count will be the same as after 15 minutes because the bacteria stop growing at -47°C.
Therefore, Shreya will have 393,216 bacteria at the end of the third experiment.
Question 1196669: DATA LINK: https://imagizer.imageshack.com/img924/7537/If85YO.png
https://imagizer.imageshack.com/img922/9241/hUOEdV.png
Is economic growth in the developing world related to growth in the industrialized countries? A scatterplot of the growth (in % of Gross Domestic Product) of the least developed countries (as classified by the UN) vs. the growth of a number of industrialized countries is provided. Each point represents a year from the past few decades. The output of a regression analysis is also provided. Complete parts a through c below.
Answer by ElectricPavlov(122) (Show Source):
You can put this solution on YOUR website! **a) Describe the relationship between economic growth in the least developed countries and the growth in industrialized countries.**
* **Examine the Scatterplot:**
* **Positive Relationship:** If the scatterplot shows a general upward trend (points sloping upwards from left to right), it suggests that economic growth in industrialized countries tends to be associated with economic growth in the least developed countries.
* **Negative Relationship:** If the scatterplot shows a downward trend, it indicates that growth in industrialized countries is associated with slower growth in the least developed countries.
* **No Relationship:** If the points are scattered randomly with no clear trend, it suggests little or no relationship between the two.
* **Consider the Regression Analysis Output:**
* **Coefficient of the Industrialized Country Growth:**
* A positive coefficient suggests a positive relationship.
* A negative coefficient suggests a negative relationship.
* **Significance of the Coefficient:**
* A statistically significant coefficient (usually indicated by a low p-value) provides evidence that the relationship between the two growth rates is not due to random chance.
**b) Interpret the slope of the regression line.**
* **Slope:** The slope of the regression line represents the estimated change in the growth rate of the least developed countries for each 1% increase in the growth rate of industrialized countries.
* **Example:** If the slope is 0.5, it suggests that for every 1% increase in the growth rate of industrialized countries, the growth rate of the least developed countries is estimated to increase by 0.5%.
**c) Discuss the limitations of using this analysis to predict the growth of the least developed countries.**
* **Correlation does not imply causation:** Even if a strong relationship is found, it doesn't necessarily mean that growth in industrialized countries directly causes growth in the least developed countries. Other factors could be influencing both.
* **External factors:** Global economic shocks, political instability, natural disasters, and other external factors can significantly impact growth in both developed and developing countries, which may not be fully captured by the model.
* **Heterogeneity among countries:** The analysis treats all least developed countries as a single group, ignoring the significant diversity within this group in terms of economic structure, resources, and development levels.
* **Time-varying relationships:** The relationship between the growth rates of developed and developing countries may not be constant over time. Factors like globalization, technological advancements, and changing trade patterns can alter the nature of this relationship.
**In summary:**
* The scatterplot and regression analysis can provide insights into the potential relationship between economic growth in industrialized and least developed countries.
* However, it's crucial to interpret the results cautiously and consider the limitations of the analysis.
**Note:** To provide more specific answers, I would need to see the actual scatterplot and the regression analysis output.
Question 1205323: Siti has RM450000 in her ASB. She wants to invest in Gading Mutual deposit, Maju
Makmur bar gold, Indah certificate deposit and Selamat Maju bar gold which pay
simple annual interest of 9%, 6%, 10% and 15%, respectively. Moreover, she wants
to combine annual return of 8% and want to have only one-third of investment in
Indah certificate deposit and Selamat Maju bar gold.
a. Write the linear model system equation for the whole investment.
c. Use elimination method to find each of the investment
Answer by CPhill(1987) (Show Source):
You can put this solution on YOUR website! ## Setting up the Linear Model
**Let's denote:**
* **G:** Amount invested in Gading Mutual Deposit
* **M:** Amount invested in Maju Makmur Bar Gold
* **I:** Amount invested in Indah Certificate Deposit
* **S:** Amount invested in Selamat Maju Bar Gold
**Based on the given information, we can set up the following system of linear equations:**
1. **Total Investment:** G + M + I + S = 450000
2. **Total Annual Return:** 0.09G + 0.06M + 0.10I + 0.15S = 0.08 * 450000
3. **Indah and Selamat Maju Investment:** I + S = (1/3) * 450000
## Solving the System Using Elimination Method
**Step 1: Simplify the Equations**
* Equation 2: 9G + 6M + 10I + 15S = 360000
* Equation 3: I + S = 150000
**Step 2: Eliminate a Variable**
* Let's eliminate S. From Equation 3, we can express S as:
* S = 150000 - I
* Substitute S in Equations 1 and 2:
* Equation 1: G + M + I + (150000 - I) = 450000
=> G + M + 150000 = 450000
* Equation 2: 9G + 6M + 10I + 15(150000 - I) = 360000
=> 9G + 6M - 5I = -750000
**Step 3: Simplify the Equations Further**
* Equation 1: G + M = 300000
* Equation 2: 9G + 6M - 5I = -750000
**Step 4: Eliminate Another Variable**
* Let's eliminate M. Multiply Equation 1 by -6 and add it to Equation 2:
* -6G - 6M = -1800000
* 9G + 6M - 5I = -750000
* -------------------------
* 3G - 5I = -2550000
**Step 5: Solve for G and I**
* From Equation 1, we can express M as:
* M = 300000 - G
* Substitute M in the simplified Equation 2:
* 3G - 5I = -2550000
* 3G - 5(150000 - G) = -2550000
* 8G = 1200000
* G = 150000
* Substitute G in M = 300000 - G:
* M = 300000 - 150000 = 150000
* Substitute G in I + S = 150000:
* I + S = 150000
* I + (150000 - I) = 150000
* S = 0
Therefore, the investments are:
* Gading Mutual Deposit: RM150,000
* Maju Makmur Bar Gold: RM150,000
* Indah Certificate Deposit: RM150,000
* Selamat Maju Bar Gold: RM0
Question 1209141: Carly just opened her own nail salon. Based on experience, she knows that her daily profit, P, in dollars, can be modelled by the relation P=-15x^2+240x-640, where x is number of clients per day. How many clients should she book each day to maximize her profit?
Answer by ikleyn(52858)  (Show Source):
You can put this solution on YOUR website! .
Carly just opened her own nail salon. Based on experience, she knows that her daily profit, P,
in dollars, can be modelled by the relation P=-15x^2+240x-640, where x is number of clients
per day. How many clients should she book each day to maximize her profit?
~~~~~~~~~~~~~~~~~~~~
The given function is a quadratic function.
Since the coefficient at x^2 is negative, the parabola is downward and has a maximum.
The maximum value is achieved a 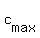 =  , where "a" is the coefficient at x^2
and "b" is the coefficient at x. In your case,
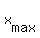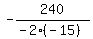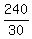 =  =  = 8.
Hence, the profit is maximum if Carly books 8 clients per day. ANSWER
Solved.
--------------------
On finding the maximum/minimum of a quadratic function see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Learn the subject from there once and for all.
Question 1208966: the numbers on the houses on the north side of carlito street are consecutive odd starting with 1. The plastic digits used to label each house are $0.04 per digit. If it costs $58.12 to label all the houses on the north side of Carlito street, how many houses are there?
Found 3 solutions by Alan3354, mccravyedwin, ikleyn:
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! Not a solution the this problem, but:
-------------
Our address at work is 910 Industrial Blvd.
A guy game in, asked for help finding his customer.
Asked me where 909 Industrial was.
Obviously, it was directly across the street.
I told him that, went out front and pointed to it.
He was grateful.
He was driving a "big rig," 18 wheeler.
===============
How can a person making deliveries for living not know about odd and even addresses?
I considered explaining that to him, but decided not to.
Probably then, "How do you know if an address is odd or even?"
There is no lower limit to intelligence.
Answer by mccravyedwin(408)  (Show Source):
You can put this solution on YOUR website!
Let's pretend they put plastic digits on ALL the houses on both sides of the
street. and that there are the same number of houses on both sides of the
street.
The number of digits in all the even integers 0,2,...,2n is the same as the
number of digits in all the odd integers 1,3,...,2n+1
It would have cost twice as much, $58.12x2 = $116.24, to put plastic digits on
all the houses on both the north and south sides of the street, that is, IF the
first even-numbered house were numbered 0.
[Even though 0 is not normally used as a house number, let's pretend it is
on this street anyway.]
If we consider 0 as a 1-digit number, then
there are 10 1-digit numbers which would cost $0.04x10=$0.40,
there are 100-10=90 2-digit numbers which would cost $0.04x2x90=$7.20,
and there are 1000-100=900 3-digit numbers which would cost $0.04x3x900=$108.
That would cost $0.40+$7.20+$108=$115.60
Since $116.24-115.60=$0.64, that means they placed $0.64/$0.04 = 16 more
plastic digits than they placed on houses numbered with 3 or fewer digits.
So 16 plastic digits were placed on 4 houses with 4-digit numbers.
These are the houses numbered 1000, 1001, 1002, and 1003.
So the even house numbers are 0,2,4,...,1002 and there are 1002/2=501 of them.
The odd house numbers are 1,3,5,...,1003 and there are also 501 of them.
Answer: There are 501 odd numbered houses on the north side of the street.
Edwin
Answer by ikleyn(52858) (Show Source):
You can put this solution on YOUR website! .
The numbers on the houses on the north side of Carlito street are consecutive odd starting with 1.
The plastic digits used to label each house are $0.04 per digit. If it costs $58.12 to label
all the houses on the north side of Carlito street, how many houses are there?
~~~~~~~~~~~~~~~~~~~
The number of the digits bought is 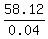 = 1453.
Of them, 5*1 = 5 digits are for five 1-digit odd numbers from 1 to 9; 1453-5 = 1448 digits left.
45*2 = 90 digits are for 45 2-digit odd numbers from 11 to 99; 1448-90 = 1358 digits left.
450*3 = 1350 digits are for 450 3-digit odd numbers from 101 to 999; 1358-1350 = 8 digits left.
These 8 digits are for two the 4-digit odd numbers 1001 and 1003 on the north side of Carlito street.
The total number of houses on the north side of Carlito street is 5 + 45 + 450 + 2 = 502. ANSWER
Solved.
////////////////////
Below is my comment regarding Edwin' solution to this problem.
The solution by Edwin, giving the answer 501 for the number of houses
with odd plates on them - is INCORRECT.
The Edwin's error is in the last two sentences in his post before the word Answer :
he incorrectly counted even numbers from 0 to 1002, inclusively,
and incorrectly counted odd numbers from 1 to 1003, inclusively.
The correct count for even numbers/plates from 0 to 1002, inclusively, is 502,
as well as the correct count for odd numbers/plates from 1 to 1003, inclusively, is 502.
Question 1207297: Xavier works in an amusement park and is helping decorate it with strands of lights. This morning, he used a total of 28 strands of lights to decorate 4 bushes and 1 tree. This afternoon, he strung lights on 3 bushes and 1 tree, using a total of 24 strands. Assuming that all bushes are decorated one way and all trees are decorated another, how many strands did Xavier use on each
Answer by ikleyn(52858) (Show Source):
You can put this solution on YOUR website! .
Xavier works in an amusement park and is helping decorate it with strands of lights.
This morning, he used a total of 28 strands of lights to decorate 4 bushes and 1 tree.
This afternoon, he strung lights on 3 bushes and 1 tree, using a total of 24 strands.
Assuming that all bushes are decorated one way and all trees are decorated another,
how many strands did Xavier use on each
~~~~~~~~~~~~~~~~
This problem ideally suits to solve it MENTALLY.
As you read the problem, you should notice in your mind, that the difference
between work done in the morning and in the afternoon is 4-3 = 1 bush and 28-24=4 strands of lights.
So, you conclude that Xavier uses 4 strands of lights to decorate each bush.
Thus this morning he used 4*4 = 16 strands of lights to decorate 4 bushes,
and the rest 28-16 = 12 strands of lights to decorate one tree.
ANSWER. 4 strands of lights for each bush and 12 strands of lights for each tree.
CHECK the number of strands of lights used in the afternoon: 4*3+12 = 24. ! correct !
Solved.
Question 1207277: DR stein bought 30 notebooks 60 pencils and 300 erasers to make identical packages with some notebooks some pencils and some erasers for his students he used everything bought and every student got a package. what is the greatest number of students in Dr stein can have in his class?
Answer by MathLover1(20850)  (Show Source):
Question 1206208: Given the following equality:
g(x) + g(x + 3) = 2x + 5
And:
g(2) + g(8) = 12
Find:
g(5)
Thanks
Answer by ikleyn(52858) (Show Source):
You can put this solution on YOUR website! .
Given the following equality:
g(x) + g(x + 3) = 2x + 5
And:
g(2) + g(8) = 12
Find g(5).
~~~~~~~~~~~~~~~~~~~~~
Take x= 2. Then from the formula g(x) + g(x + 3) = 2x + 5 you have
g(2) + g(5) = 9. (1)
Take x= 5. Then from the formula g(x) + g(x + 3) = 2x + 5 you have
g(5) + g(8) = 15. (2)
Add equations (1) and (2). You will get
g(2) + 2*g(5) + g(8) = 24.
Replace here g(2) + g(8) by 12 (since it is given in the problem). You will get
12 + 2*g(5) = 24 ---> 2*g(5) = 24-12 = 12 ---> g(5) = 12/2 = 6.
ANSWER. g(5) = 6.
Solved.
Question 1206112: In a mixture of copper, tin, and lead, one half of the whole, minus 16 lb, was copper; one third of the whole, minus 12 lb, was tin, and one fourth of the whole, plus 4 lb, was lead: how much did the whole mixture weigh?
Answer by josgarithmetic(39626) (Show Source):
You can put this solution on YOUR website! One can transcribe the description exactly as written,
here using w for the whole quantity of mixture.
Copper (w/2)-16
Tin (w/3)-12
Lead (w/4)+4
WHOLE w
.
.
Another way, the whole mixture is some 12 equal parts, so 12M is this mixture quantity.
Copper 6M-16
Tin 4M-12
Lead 3M+4
WHOLE 12M
Remember M here is a factor.
Equation to solve can be  .
.
.
Question 1205729: A cruise ship had 3 times as many adult passengers as child passengers when it left its first port. At a new port, 116 adults and 50 children boarded the ship. There are now 1,216 more adults than children on the ship. How many children were on the ship at first?
Found 3 solutions by josgarithmetic, greenestamps, MathLover1:
Answer by josgarithmetic(39626) (Show Source):
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Let x = number of children at first
Then 3x = number of adults at first
x+50 = number of children after the new port
3x+116 = number of adults after the new port
The number of adults is now 1216 more than the number of children:
Solve using basic algebra; I leave the work to you. (Re-post, showing your work, if you don't get the answer below.)
ANSWER: 575 children and 1725 adults at first
Answer by MathLover1(20850) (Show Source):
Question 1205480: if a + b = -3 and b - c = 6, find the value of 
Found 3 solutions by ikleyn, math_tutor2020, greenestamps:
Answer by ikleyn(52858) (Show Source):
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
This is a system of 2 equations with 3 unknowns.
The fact we have more unknowns than equations leads to "infinitely many solutions" for this system.
It turns out that each solution is of the form (a,b,c) = (-9-c,6+c,c) which I explain in a later section below.
Let's say c = 0
b-c = 6
b-0 = 6
b = 6
Then,
a+b = -3
a+6 = -3
a = -3-6
a = -9
Or you could say
(a,b,c) = (-9-c,6+c,c)
(a,b,c) = (-9-0,6+0,0)
(a,b,c) = (-9,6,0)
Therefore,
------------------------------------------------------------
Another example
Let c = 1
b-c = 6
b-1 = 6
b = 6+1
b = 7
Then,
a+b = -3
a+7 = -3
a = -3-7
a = -10
Or
(a,b,c) = (-9-c,6+c,c)
(a,b,c) = (-9-1,6+1,1)
(a,b,c) = (-10,7,1)
Therefore,
------------------------------------------------------------
One more example
Let's say c = 2
b-c = 6
b-2 = 6
b = 6+2
b = 8
Then,
a+b = -3
a+8 = -3
a = -3-8
a = -11
Or
(a,b,c) = (-9-c,6+c,c)
(a,b,c) = (-9-2,6+2,2)
(a,b,c) = (-11,8,2)
Therefore,
It appears we keep landing on 54.
Is this a coincidence? Or is this always going to happen?
The next section will shed light on that.
------------------------------------------------------------
A more generalized approach.
b-c = 6
b = 6+c
a+b = -3
a+(6+c) = -3
a = -3-6-c
a = -9-c
We have
a = -9-c
b = 6+c
c = c
in which we can say
(a,b,c) = (-9-c,6+c,c)
This confirms that the system a+b = -3 and b-c = 6 has infinitely many solutions.
So,
This proves that if a+b = -3 and b-c = 6, then will always land on 54.
--------------------------------------------------------------------------
--------------------------------------------------------------------------
Answer: 54
Answer by greenestamps(13203) (Show Source):
Question 1205373: The perimeter of a rectangle is 48cm. The length of a rectangle is 3cm longer than twice its width. Find the dimensions of the rectangle.
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
Answer: 17 cm by 7 cm
Work Shown
w = width
2w+3 = length
2*(length + width) = perimeter of rectangle
2*(2w+3 + w) = 48
2*(3w+3) = 48
6w+6 = 48
6w = 48-6
6w = 42
w = 42/6
w = 7 cm is the width
2w+3 = 2*7+3 = 17 cm is the length
Check:
perimeter = 2*(length+width) = 2*(17+7) = 2*24 = 48 cm
We have confirmed the answers.
Question 1205305: A farmer has fenced off his trapezoidal housing area, which is shown in the diagram. There is a post at each of the point A and B, to which the farmer sometimes attaches a 30m rope that is tied to his donkey. This provides the donkey either one of two grazing areas outside the housing area. Find the difference in the areas available for grazing in square meters (m^2)
Found 2 solutions by math_tutor2020, Edwin McCravy:
Answer by math_tutor2020(3817) (Show Source):
Answer by Edwin McCravy(20060)  (Show Source):
Question 1205272: Abu compares package postpaid mobile plans between Remaja Hebat Plan and
Unlimited Plan. Remaja Hebat Plan charges RM0.05 per minutes plus a basic
monthly fee for RM 7.50. Unlimited Plan charges RM 0.075 per minute plus a basic
monthly fee of RM4.25
a. Write the model for package postpaid mobile plans for Remaja Hebat Plan
and Unlimited Plan.
b. Identify the best mobile plan.
c. Sketch the graph for package postpaid mobile plans between Remaja Hebat
Plan and Unlimited Plan
. Alia rows a boat upstream from one point on a river to another point 4 km away in 1.5 hours.
The return trip, traveling with the current, takes only 45 min.
a. Identify the variables involve in algebra.
b. Find the speed of the current flowing by using back-substitution method
Answer by ikleyn(52858) (Show Source):
You can put this solution on YOUR website! .
Do not pack more than 1 (one) problem per post.
It is against the rules of this forum; against the common sense,
perpendicular to the rules of good behavior and against your own interests.
For the rules of this forum, read at this web-page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you post your problems. Read it attentively and find many useful instructions there.
Become a civilized user / visitor . . .
Question 1204788: There were 1200 persons at a crusade, 8004 of them were women of the remaining persons persons,there were 3 times as many children as men. How many children were there?
Found 2 solutions by mananth, MathLover1:
Answer by mananth(16946)  (Show Source):
You can put this solution on YOUR website! There were 1200 persons at a crusade, 8004 of them were women of the remaining persons,there were 3 times as many children as men. How many children were there?
There is a typing error check and repost
Answer by MathLover1(20850) (Show Source):
Question 1204616: For a cylinder with a surface area of 10
, what is the maximum volume that it can have? Round your answer to the nearest 4 decimal places.
Recall that the volume of a cylinder is πr2h
and the surface area is 2πrh+2πr2
where r
is the radius and h
is the height.
Answer by math_tutor2020(3817) (Show Source):
Question 1204598: System of equations:
-7x+3y=-65
-7x+10y=-135
Write an equation that results from subtracting two equations
Answer by ikleyn(52858) (Show Source):
You can put this solution on YOUR website! .
System of equations:
-7x+3y=-65
-7x+10y=-135
Write an equation that results from subtracting two equations
~~~~~~~~~~~~~~~~~~~~~~~~~
If you subtract first equation from the second equation, the resulting equation will be
10y - 3y = -135 - (-65),
or
7y = -135 + 65,
or
7y = -70 <<<---=== final
Subtracted and explained.
Question 1204043: The sum of two numbers is -22. The difference of the two numbers is 8. What are the  numbers?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13203) (Show Source):
You can put this solution on YOUR website!
The solution shown by tutor @ikleyn is probably the easiest, most straightforward way to solve the problem using formal algebra.
Of the many other ways to solve the problem that she mentions, there is one that I find to be a quick and easy informal method, using logical reasoning and simple mental arithmetic.
We are given that the sum of two numbers is -22 and the difference is 8.
If we picture that on a number line, then we start at the first number and go a distance equal to the second number in one direction to end up at -22, and we start at the first number and go a distance equal to the second number in the other direction to end up at 8.
That means the first number is halfway between -22 and 8.
So the first number is the average of -22 and 8; and then the second number is the difference between that average and either -22 or +8.
First number: (-22+8)/2 = -7
Second number: (-22)-(-7) = -15 (or (-7)-(8) = -15)
ANSWERS: -7 and -15
Answer by ikleyn(52858) (Show Source):
You can put this solution on YOUR website! .
x + y = -22
x - y = 8
------------------- Add these equations to get
2x = -22 + 8 = -14 ---> x = -14/2 = -7; y = -22 - x = -22 - (-7) = -22 + 7 = -15.
ANSWER. The numbers are -7 and -15.
Solved.
There are other ways to solve, but this one is the most educative (in my view).
Question 1204044: The sum of two numbers is -22. The difference of the two numbers is 8. What are the two numbers?
Answer by ikleyn(52858) (Show Source):
You can put this solution on YOUR website! .
x + y = -22
x - y = 8
------------------- Add these equations to get
2x = -22 + 8 = -14 ---> x = -14/2 = -7; y = -22 - x = -22 - (-7) = -22 + 7 = -15.
ANSWER. The numbers are -7 and -15.
Solved.
There are other ways to solve, but this one is the most educative (in my view).
Question 1202975: A wire 80 cm in length is cut into two parts and each part is bent to form a square. If the sum of the areas of the squares is 300 cm?, find the lengths of the sides of the two squares
Answer by math_helper(2461)  (Show Source):
Question 1202774: In what ways can you change a $100 bill using $10 bills, $5 bills, and $1 bills?
Answer by greenestamps(13203) (Show Source):
You can put this solution on YOUR website!
Whether you really want a list of all the different ways, or whether you only want to know HOW MANY ways there are, I will show you HOW to solve the problem and leave the details to you.
(1) Since the $10 bills and $5 bills together make a total number of dollars that is a multiple of 5, and since the total $100 is a multiple of 5, the total value of the $1 bills must be a multiple of 5.
(2) For each number of $1 bills that is a multiple of 5, the number of ways to make change for $100 is determined by the number of $10 bills you can have. For example, if there are 55 $1 bills, then the remaining amount is $45, and you can use 0, 1, 2, 3, or 4 $10 bills, making up the rest with $5 bills. That makes 5 ways to make change for $100 if the number of $1 bills is 55.
To outline the complete solution, then....
column 1: # of $1 bills
column 2: remaining amount
column 3: # of choices for the number of $10 bills
0 100 11 (0 to a maximum of 10)
5 95 10 (0 to a maximum of 9)
10 90 10 (0 to a maximum of 9)
...
...
85 15 2 (0 to a maximum of 1)
90 10 2 (0 to a maximum of 1)
95 5 1 (only 0)
100 0 1 (only 0)
Add the numbers in column 3 to find the total number of ways of making change for $100 using $10, $5, and $1 bills.
Note there is a nice pattern in the numbers in column 3 that makes it possible to find the total without adding the numbers one at a time....
Question 1202599: Write an exponential model for the following situation. The drug dosage is 375 mg. The drug is eliminated at a rate of 11.3% per hour. Use D=the amount of the drug in milligrams and t=time in hours. Enter your model in the simplified form y=asup(bracket(b),x), and be mindful about the case of your variables.
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52858) (Show Source):
You can put this solution on YOUR website! .
Write an exponential model for the following situation.
The drug dosage is 375 mg. The drug is eliminated at a rate of 11.3% per hour.
Use D=the amount of the drug in milligrams and t=time in hours.
Enter your model in the simplified form y=asup(bracket(b),x),
and be mindful about the case of your variables.
~~~~~~~~~~~~~~~~~~
Below I present for you a STANDARD mantra on how to solve such problems.
The starting amount of the drug is 375 mg, and the exponential rate of eliminating the drug
is 11.3% per hour. It means that in terms of (D,t) the exponential model is
D = 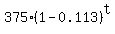 =  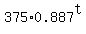. (1)
Here 375 is the initial/starting amount, given in this problem;
1-0.113 = 0.887 is the reducing factor per hour; t is the time, in hours.
+-----------------------------------------------------------------+
| Again, knowing the starting amount and the exponential rate |
| is just ENOUGH to write an exponential model (1) in whole. |
+-----------------------------------------------------------------+
In (y,x) form, formula (1) becomes
y =  .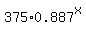
That is all the mantra.
You do not need to pronounce any more words, because excessive words are UNNECESSARY and IRRELEVANT.
Moreover, if you will pronounce excessive words, everybody around will understand immediately
that you do not know the subject and that nobody and never did explain the subject to you in a right way.
-------------------
To see many other similar and different solved problems, look into the lesson
- A medication decay in a human's body
in this site.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! the drug dose is 375 milligrams.
the drug is eliminated at a rate of 11.3% per hour.\
D = amount of drug in milligrams.
t = time in hours.
the equation i use most for these if f = p * (1 + r) ^ n
f is the future value
p is the present value
r is the growth rate per time period
(1 + r) is the growth factor per time period.
n is the number of time periods.
in your problem:
p would be equal to 375 milligrams.
r would be -.113 per hour.
(1 + r) would be (1 - .113) = .887 per hour.
n would be the number of hours.
the formula would be simplified to f = 375 * .887 ^ n
replacing f with D and n with t, the formula would becomes D = 375 * .887 ^ t.
this would be you solution to this problem.
if i graph that formula, i would replace D with y and t with x to get y = 375 * .887 ^ x
here's what the graph would look like.
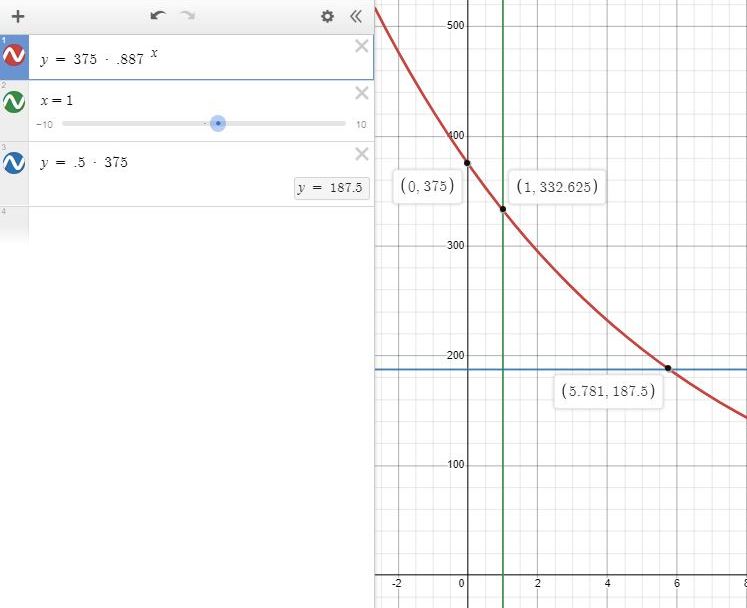
the amount of drug after 1 hours would be D = 375 * .887 ^ 1 = 332.675, as shown in the graph.
the half life of the drug would be calculated as follows:
D = 375 * .887 ^ t becomes 187.5 = 375 * .887 ^ t.
divide both sides of the equation by 187.5 to get .5 = .887 ^ t.
take the log of both sides of the equation to get:
log(.5) = log(.887 ^ t)
by log rule that says log(x^t) equals t * log(x), the formula becomes log(.5) = t * log(.887).
divide both sides of the equation by log(.887) to get log(.5) / log(.887) = t
solve for t to get t = 5.780547624.
round to 3 decimal placdes to get t = 5.781
this agrees with what's on the graph.
don't forget that D is the same as y on the graph and t is the same as x on the graph.
i don't know what y=asup(bracket(b),x), stands for.
a form of the exponential equation would be y = ab^x
if that's the case, then a would be 375 and b would be .887.
y = ab^x would then be y = 375 * .887 ^ x
this is the same as D = 375 * .887 ^ t, with y representing D and x representing t.
let me know if you have any questions.
theo
Question 1202419: There was $2900 in the pot. If there were 293 more $1 bills than $10 bills, how many bills of each kind were there?
Found 4 solutions by josgarithmetic, greenestamps, mananth, math_tutor2020:
Answer by josgarithmetic(39626) (Show Source):
Answer by greenestamps(13203) (Show Source):
You can put this solution on YOUR website!
Here is an informal solution using logical reasoning and simple arithmetic. Compare it to the solution from tutor @math_tutor2020 to see that the formal algebra does exactly what the informal solution does.
Subtract the "extra" 293 $1 bills from the total, leaving equal numbers of $1 and $10 bills with a total value of $2900-$293 = $2607.
The total value of one $1 bill and one $10 bill is $11.
So the number of bills of each kind remaining is $2607/$11 = 237.
ANSWERS:
$10 bills: 237
$1 bills: 237+293 = 530
CHECK: 237(10)+530(1) = 2370+530 = 2900
Answer by mananth(16946) (Show Source):
You can put this solution on YOUR website! There was $2900 in the pot. If there were 293 more $1 bills than $10 bills, how many bills of each kind were there?
Let number of $ 10 be x
Number of $ 1 bills = x+293
Total amout = $2900
Equation of amount
10x+1$(x+293) = 2900
10x+x+293 =2900
11x = 2607
x = 237
complete it
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
x = number of ten dollar bills
x+293 = number of one dollar bills
1*(x+293) = x+293 = total value of all the $1 bills only
10x = total value of all the $10 bills only
(x+293)+(10x) = 11x+293 = total value in dollars of both type of bills combined
total = $2900
11x+293 = 2900
11x = 2900-293
11x = 2607
x = 2607/11
x = 237 is the number of $10 bills
x+293 = 530 is the number of $1 bills
Check:
A = 530 one dollar bills = 530*1 = $530
B = 237 ten dollar bills = 237*10 = $2370
A+B = $530+$2370 = $2900
Solution is verified.
Answer:
530 one dollar bills
237 ten dollar bills
Question 1202283: Peaches were $7 a bushel and apples were $6 a bushel. Harry sold $346 worth and sold 29 more bushels of peaches than apples. How many bushels of each did he sell?
Found 3 solutions by josgarithmetic, greenestamps, ikleyn:
Answer by josgarithmetic(39626) (Show Source):
Answer by greenestamps(13203) (Show Source):
You can put this solution on YOUR website!
While the problem was probably supposed to be solved using formal algebra, note that you can get good mental exercise by solving the problem informally, using logical reasoning and mental arithmetic.
The 29 "extra" bushels of peaches cost 29($7) = $203.
The remaining $346-$203 = $143 was the cost of equal numbers of bushes of peaches and apples.
The cost of one bushel each of peaches and apples was $13.
$143/$13 = 11, so the purchase after the "extra" bushels of peaches consisted of 11 bushels each of peaches and apples.
So the number of bushels of apples he sold was 11, and the number of bushels of peaches he sold was 11+29 = 40.
ANSWER: 11 bushels of apples and 40 bushels of peaches
CHECK: 11($6)+40($7) = $66+$280 = $346
Answer by ikleyn(52858) (Show Source):
You can put this solution on YOUR website! .
Peaches were $7 a bushel and apples were $6 a bushel.
Harry sold $346 worth and sold 29 more bushels of peaches than apples.
How many bushels of each did he sell?
~~~~~~~~~~~~~~
Let x be the number of bushels of apples.
Then the number of bushels of peaches is (x+29).
Write the total money equation
7(x+29) + 6x = 346.
Simplify and find x
7x + 7*29 + 6x = 346
7x + 6x = 346 - 7*29
13x = 143
x = 143/13 = 11.
ANSWER. 11 bushels of apples and (11+29) = 40 bushels of peaches.
CHECK the total revenue 7*40 + 6*11 = 280 + 66 = 346 dollars. ! correct !
Solved.
Question 1201889: Two data sets have the same range, can you assume the interquartile ranges are about the same? Please include an example to justify your answer.
Also, I'm sorry I don't know what the topic would be "(
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
Consider this seven element list
{1,2,3,4,5,6,7}
The median is 4 because it's the middle most value.
This can be seen fairly quickly, or we could cross off the first and last terms (1 and 7) to get {2,3,4,5,6}
Then repeat again to get {3,4,5} and at this point it's more clear 4 is at the very middle.
What's another way to find the median?
We have n = 7 items.
The midpoint is at slot 4 because (n+1)/2 = (7+1)/2 = 8/2 = 4
Or you could say n/2 = 7/2 = 3.5 which rounds to 4.
Either formula only works when n is odd.
We'll use the median to split the data into two halves
Split the data into a lower set L and upper set U
L = lower set
L = stuff smaller than the median
L = {1,2,3}
U = upper set
U = stuff larger than the median
U = {5,6,7}
The median is not part of either subset.
The median of set L is 2, which is the first quartile Q1.
The median of set U is 6, which is the third quartile Q3.
Q1 = 2
Q3 = 6
IQR = interquartile range
IQR = Q3 - Q1
IQR = 6-2
IQR = 4
And,
range = max - min
range = 7 - 1
range = 6
Summary: The data set {1,2,3,4,5,6,7} has range = 6 and IQR = 4.
-----------------------
We can add some constant to each item of that set to shift things over.
I'll add 10 to each value
{1,2,3,4,5,6,7} turns into {11,12,13,14,15,16,17}
The range is still 6 because max-min = 17-11 = 6
The IQR is still 4 because Q3 - Q1 = 16-12 = 4
This demonstrates that shifting the values the same amount won't affect the range, and won't change the IQR either.
But what if we replaced 12 and 16 with say 12.5 and 15.5 respectively?
What if we had {11,12.5,13,14,15,15.5,17}
Again the range is still 6 because max-min = 17-11 = 6
But the IQR is now different
IQR = Q3 - Q1 = 15.5-12.5 = 3
The IQR is smaller since I moved Q1 and Q3 closer together.
Earlier we had IQR = 4.
Here is a box plot, aka box-and-whisker plot, of {11,12,13,14,15,16,17} in blue
Compared to a box plot of {11,12.5,13,14,15,15.5,17} in red.
The distance from left whisker (11) to right whisker (17) is the same for both box plots.
That distance is the range 6.
However, the width of the boxes themselves aren't the same.
The red box at the bottom is slightly more skinny compared to the blue box up top.
Q1 = left edge of the box
Q3 = right edge of the box
IQR = Q3 - Q1 = distance from Q1 to Q3 = width of the box (ignore whiskers)
Conclusion: Two data sets having the same range does NOT guarantee the IQR's will be the same.
Question 1201657: A farmer can plow a field in 24 hours. His son, with a larger plow, can plow it in 12 hours. The farmer asked that they work together so they could finish before the rain started. It rained 7 hours later. Had they finished plowing before the rain?
Answer by ikleyn(52858) (Show Source):
Question 1201636: One conveyor belt can move 1000 boxes in 11 minutes. Another can move 1000 boxes in 3 minutes. If another conveyor belt is added and all three are used, the boxes are moved in 3 minutes. How long would it take the third conveyor belt alone to do the same job?
Found 2 solutions by josgarithmetic, greenestamps:
Answer by josgarithmetic(39626) (Show Source):
Answer by greenestamps(13203) (Show Source):
You can put this solution on YOUR website!
No calculations are necessary; the problem is clearly faulty.
The second conveyor belt alone can move all the boxes in 3 minutes. The first conveyor belt is not needed; and there is certainly no need to add a third.
Question 1201249: Jodi is paid by commission as a salesperson. She earns 5% commission for each laptop computer she sells and 8% commission for each DVD player she sells. Suppose that the average price of a laptop is $600 and the average price of a DVD player is $200.
a) What is the average amount Jodi earns for selling each item?
b) Jodi wants to earn a minimum commission this month of $1000. Write an inequality to represent this situation.
Answer by greenestamps(13203) (Show Source):
You can put this solution on YOUR website!
Earnings for selling a laptop: 5% of $600 = .05($600) = $30
Earnings for selling a DVD player: 8% of $200 = .08($200) = $16
x = # of laptops sold
y = # of DVD players sold
Question 1201379: Patty takes two hours to ice a cake alone, whereas Bob takes three hours to ice a cake alone. The number of hours it would take Patty and Bob working together to ice a cake is
a) 1 1/5 b) 1 1/4 c) 1 1/3 d) 2 1/2 e) 5
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
Let's say the cake's surface area is 60 square inches.
I picked a value that is a common multiple between 2 and 3 (since 2*3 = 6).
It turns out that the surface area doesn't matter since we'll get the same answer for other surface area values.
Feel free to pick some other positive number.
Patty takes 2 hours to cover 60 square inches when working alone.
Her rate is 60/2 = 30 sq in per hour.
The formula I used is:
rate = (amount done)/(time)
Bob takes 3 hours to cover 60 square inches when working alone.
His rate is 60/3 = 20 sq in per hour.
Their combined rate is 30+20 = 50 sq in per hour.
If the two team up, and don't get in each other's way, then their combined rate is 50 sq in per hour.
Let's determine how long they take when working together.
rate = (amount done)/(time)
rate*time = amount done
time = (amount done)/(rate)
time = (60 sq in)/(50 sq in per hr)
time = (60/50) hr
time = (6/5) hr
time = ( (5+1)/5 ) hr
time = ( 5/5 + 1/5 ) hr
time = ( 1 + 1/5 ) hr
Side notes:
1 hr + 1/5 hr = 1 hr + 0.2 hr = 1.2 hr
or
1 hr + 1/5 hr = 60 min + (1/5)*(60) min = 60 min + 12 min = 72 min
or
1 hr + 1/5 hr = 1 hr + 12 min
Answer: Choice A) 1 1/5
This is the mixed number 1 & 1/5
whole part = 1
fractional part = 1/5
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915
|
| |
