Question 920749: 12x^2-29x+15=0 ( Factor)
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39615)   (Show Source): (Show Source):
You can put this solution on YOUR website! Try thinking of the quadratic trinomial this way.

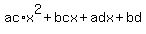
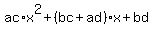
Compare the coefficients to form the equations:
ac=12, -29=bc+ad, bd=15
Three equations but FOUR unknown variables. You at least expect a,b,c,d to all be integers, and be nonzero.
You can make logical trials and test them.
a and c not relying on order nor sign, would be one of 1 & 12; 2 &6, 3 & 4.
b and d similarly would be one of 1 & 15, or 3 & 5.
Do what you are able with those facts.
A more advanced way to factorize is to use the discriminant:
 , ,
 ; ;
This means that the ROOTS for x are 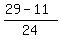 and and 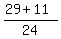 ; ;
or,  and and  ; ;
This then means you can choose a form for your quadratic expression,
 , which you could refactor if you want to. , which you could refactor if you want to.
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website! 12x^2-29x+15=0 ( Factor)Using the "ac" method to factor the left-side trinomial, we need to find 2 factors with a
PRODUCT of + 180 (+ 12 * + 15), and a sum of - 29 (b). These 2 factors are: - 20 and - 9
12x2 - 29x + 15 = 0 becomes:
12x2 - 20x - 9x + 15 = 0 ------- Replacing - 29x with - 20x - 9x
4x(3x - 5) - 3(3x - 5) = 0 ------ Factoring out the GCF of the 1st 2 terms, and the 2nd 2 terms
(4x - 3)(3x - 5) = 0 ------------- Factored form of the trinomial
4x - 3 = 0 OR 3x - 5 = 0
From here, you can determine the 2 values of x, if that's your goal.
|
|
|