Question 762164: Write and solve the system of equations algebraically to determine where the two cost options are equivalent showing all work.
Garage A – Monthly Unlimited Parking Pass: $150
Garage B - Hourly Parking Rate: $1.25/ hour (no max)
Additional info- for hourly, the employee will work 8 hour days, 20 days per month.
Let Y= Total amount per month
Let Z= Number of hours per day
Let W= Number of working days in a month; estimated 20.
This is what I have:
Equal Parking Fee (monthly vs hourly)
Y= Monthly Rate
Y=150
$150=(1.25z)20
-$1.25 x Z x 20+$150= 0
-25Z+$150=0
Feedback received:
An algebraic process has been provided, but the algebra is inaccurate.
Can anyone help me?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The problem and the feedback lend themselves to different interpretations. Having dealt with online courses (taken by my son or myself), I am familiar with your kind of trouble.
You seem to be dealing with a computer, and I cannot figure out what the feedback means. It could mean that $ signs were not expected in the answer. It could mean that you used x for a multiplication sign and the computer interpreted it as a variable. It could also be that you did not interpret the problem the way it was expected to be interpreted.
Not being a computer, I see nothing wrong with your algebra. It would lead you to  , and 6 hours of parking per day, 20 days per month would certainly make the cost of both garages the same.
Your interpretation of the problem is one of many that sound reasonable to me. If the problem asks "to determine where the two cost options are equivalent" there must be some independent variable(s) that could affect the cost, which we take as dependent variable. The days parking is used, and the hours parked per day could be such variables. I assume the problem deals with a person who has to work in the city, where he/she must pay for parking, and works a regular (fixed) number of hours per day, Monday to Friday, excluding holidays, vacation days, and sick days. If driving to and from work, that person will have to pay for parking while at work. You assumed the person will need to park 20 days per month, and figured how many hours that person can park per day to make the two garages equally costly. Maybe it would have been more realistic to assume the person will park for 8 hours each day, and find how many days of parking can be used per month to make the cost the same for both garages.
Let's define
 = cost of parking for one month,
 = days parking is used in a month, and
 = hours of parking used each day.
For garage A:
For garage B:
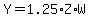
With the equations above we can set up the system
and the solution to that system,
 <-->  <-->  ,
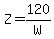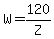gives us the points (Z,W) where the cost for both garages would be the same.
Maybe that was the expected answer.
Maybe it was  , assuming  .
If we know or estimate Z and W, using
for the hours of daily parking, and
 for the days using parking in a month,
the equation for garage B tells us the cost for garage B
 --> 
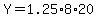so garage B is more costly with those values of W and Z,
but we are not comparing "to determine where the two cost options are equivalent", because we gave values to the variables.
Did the problem suggest those values? Or are they your own estimates?
|
|
|
