Question 1162693: On a 12-hour clock, at what precise times (in fractions of a minute or second) would the hands be at right angles (90 degrees) between 10 and 11 o'clock?
Found 2 solutions by greenestamps, Theo:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There will be two times. A few minutes after 10 o'clock, the minute hand will be 90 degrees "ahead of" the hour hand; and a few minutes after 10:30 the minute hand will be 90 degrees "behind" the hour hand.
There are many ways to solve this problem. I will show you the way I find easiest; perhaps other tutors will respond showing different ways.
In every 12-hour period, the angle between the hour hand and minute hand will be any fixed number of degrees 11 times. That is because the minute hand makes 12 revolutions in 12 hours while the hour hand makes only one.
So for any fixed measure between the hands of a clock, the times when the hands are at that angle will differ by 12/11 of an hour.
The minute hand is 90 degrees ahead of the hour hand at 9 o'clock. So the time shortly after 10 o'clock when it will be 90 degrees ahead of the hour hand will be 9 hours plus 12/11 hours, or 10 and 1/11 hours. In terms of fractions of a minute, that means 60/11 minutes after 10 o'clock.
Similarly, the minute hand is 90 degrees behind the hour hand at 3 o'clock. So the time between 10 and 11 that it is again 90 degrees behind the hour hand is 3 o'clock, plus 7 time 12/11 hours. That makes 3 + 84/11 = 3 + 7 7/11 hours = 10 7/11 hours. In terms of fractions of a minute, that is 420/11 minutes after 10 o'clock.
ANSWERS:
(1) 10 o'clock plus 60/11 minutes, or 5 5/11 minutes after 10.
(2) 10 o'clock plus 420/11 minutes, or 38 2/11 minutes after 10.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the hour hand is 300 degrees at 10:00 and 330 degrees at 11:00
there are 60 minutes between 10:00 and 11:00
therefore, the hour hand moves .5 degrees every minute.
10:00 is 300 degrees.
11:00 is 60 minutes later * .5 = 30 degrees more = 330 degrees.
this part checks out.
the minute hand moves 6 degrees every minute.
60 * 6 = 360 degrees.
this part checks out.
you want the difference between the hour hand position and the minute hand position to be either 90 degrees or 270 degrees.
since the minute hand moves 6 degrees per minute and the hour hand moves .5 degrees per minute, then the minute hand moves 12 times as far as the hour hand each minute.
you start the hour hand at 10:00 which means the hour hand is at the 300 degree position.
you start the minute hand at 12:00 which means the minute hand is at the 360 degree position.
you want the minute hand position minus the hour hand position to be equal to 90 degrees or 270 degrees.
let x = the number of degrees the hour hand moves in a minute
then 12x = the number of degrees the minute hand moves in a minute.
your formula becomes:
d = 360 + 12x - (300 + x)
simplify to get:
d = 360 + 12x - 300 - x
combine like terms to get:
d = 60 + 11x
when d = 90, the formula becomes:
90 = 60 + 11x
subtract 60 from both sides to get:
30 = 11x
solve for x to get:
x = 30/11
when d = 270, the formula becomes:
270 = 60 + 11x
subtract 60 from both sides to get:
210 = 11x
solve for x to get:
x = 210/11
when x = 30/11, you get the following:
for the hour hand, the number of degrees becomes 300 + 30/11 = 302.7272727
for the minute hand, the number of degrees becomes 360 + 12 * 30/11 = 392.7272727
the difference is 90 degrees.
when x = 210/11, you get the following:
for the hour hand, the number of degrees becomes 300 + 210/11 = 319.0909091
for the minute hand, the number of degrees becomes 360 + 12 * 210/11 = 589.0909091
the difference is 270 degrees.
for 90 degrees difference, the hour hand is at 302.7272727 degrees.
in terms of hours, the hour is therefore 302.7272727 / 360 * 12 = 10.09090909
that's roughly 10 o'clock and 5 minutes and 27 seconds.
that would be 10:05:27.
this is confirmed by the picture of the clock at 90 degrees which shows the time as 10:05:25.
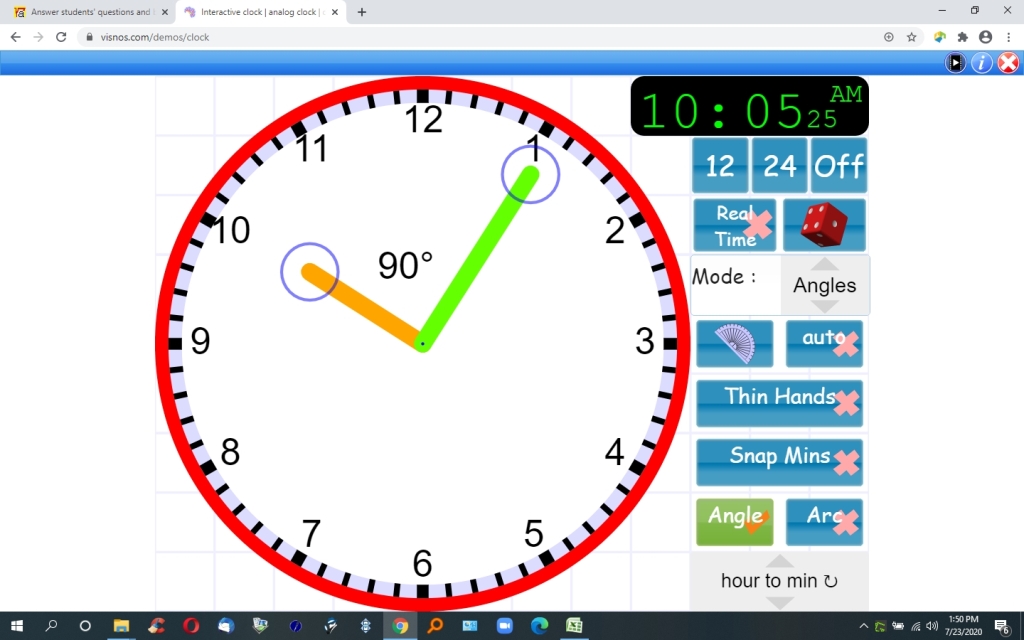
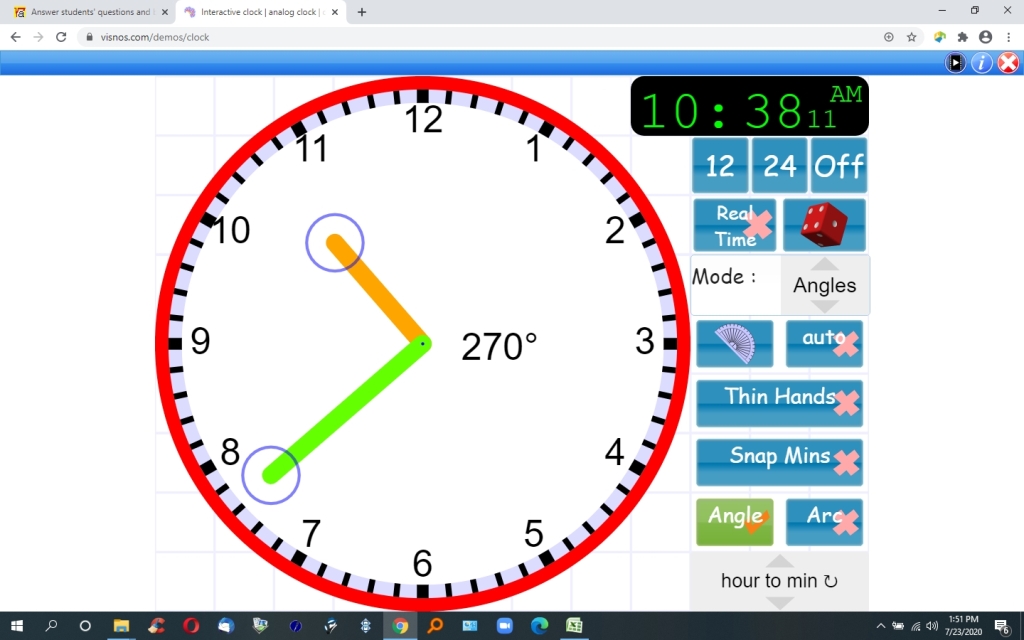
for 270 degrees difference, the hour hand is at 319.0909091 degrees
in terms of hours, the hour is therefore 319.0909091 / 360 * 12 = 10.63636364.
that's roughly 10 o'clock and 38 minutes and 11 seconds.
this is confirmed by the picture of the clock at 270 degrees which shows the time as 10:38:11
at 90 degree difference, your solution is:
10:05.454545455 or 10:05:27.27272727.
at 270 degree difference, your solution is:
10:38.18181810 or 10:38:10.90909091
the first form of the answer is in fractions of minutes.
the second form of the answer is in fractions of seconds.
both forms are based on clock times.
|
|
|