SOLUTION: Calculus Question Use implicit differentiation to find y' for x^3 + y^3 = 12xy

 = 12xy


Differentiate, considering y as a function of x, y = y(x) :


    3x^2 + 3y^2*y' = 12y + 12x*y'


Collect the terms with y' in one side;  the terms with no y' in the other side :


     3y^2*y' - 12x*y' = 12y - 3x^2


     y'*(3y^2 - 12x) = .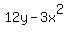


Express  y' :


     y' = ,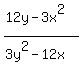   


or,  canceling the common factor 3 in the numerator and in the denominator,


     y' = ,   


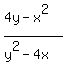It is your answer.