SOLUTION: Calculus Optimization Question An open box is to be made from a 16 cm by 30 cm piece of cardboard by cutting out a square in each of the corners. The sides are then folded up t

Algebra ->  Equations -> SOLUTION: Calculus Optimization Question An open box is to be made from a 16 cm by 30 cm piece of cardboard by cutting out a square in each of the corners. The sides are then folded up t      Log On


   

Question 1142709: Calculus Optimization Question
An open box is to be made from a 16 cm by 30 cm piece of cardboard by cutting out a square in each of the corners. The sides are then folded up to create the box. What are the optimum dimensions of the squares that should be cut out in order to maximize the volume?
Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
When the four squares at the corners are cut and the sides folded up, the base of the open box has 
dimensions  (16-2x) cm  and  (30-2x) cm,  while its height is x cm.



So, the volume of the open box is


    V(x) = x*(16-2x)*(30-2x)


    V(x) = x*(4x^2 - 92x + 480) = 4x^3 - 92x^2 + 480x.


To find the maximum volume, first take the derivative of the volume over x and then equate it to zero:


    V'(x) = 12x^2 - 184x + 480 = 0.


Simplify the equation


    3x^2 - 46x + 120 = 0.


Find the roots using the quadratic formula


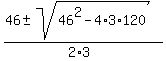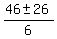x%5B1%2C2%5D = %2846+%2B-+sqrt%2846%5E2+-+4%2A3%2A120%29%29%2F%282%2A3%29 = %2846+%2B-+26%29%2F6.


The root  x%5B1%5D = %2846+%2B+26%29%2F6 = 12  is not the solution to the problem, since (16-2x) is NEGATIVE.


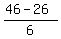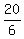x%5B2%5D = %2846+-+26%29%2F6 = 20%2F6 = 32%2F3 cm  is the solution to the problem.


ANSWER.  Optimum dimension of the squares to maximize the volume is  32%2F3 cm.


See the plot below of the volume V(x) as a function of x.



    


        Plot  V(x) = x%2A%2816-2x%29%2A%2830-2x%29