.
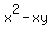 = 3 (1)
= 3 (1)
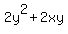 = 9 (2)
Right side of (2) is 9 = 3*3. Replace one factor of 3 by the left side of (1). You will get
= 9 (2)
Right side of (2) is 9 = 3*3. Replace one factor of 3 by the left side of (1). You will get
 =
= 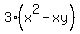 , or, equivalently
, or, equivalently
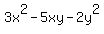 = 0. (3)
Now factor left side of (3) to get
(x-2y)*(3x+y) = 0.
Thus EITHER x-2y = 0 OR 3x+y = 0.
Lets consider each case separately.
1) x-2y = 0 ====> x = 2y ====> substitute it into eq(1) ====>
= 0. (3)
Now factor left side of (3) to get
(x-2y)*(3x+y) = 0.
Thus EITHER x-2y = 0 OR 3x+y = 0.
Lets consider each case separately.
1) x-2y = 0 ====> x = 2y ====> substitute it into eq(1) ====>  = 3 ====>
= 3 ====>  = 3
====>
= 3
====>  =
=  ====> y = +/-
====> y = +/- 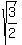 = +/-
= +/- 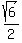 .
If y =
.
If y = 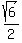 <---> x =
<---> x =  , and both equations (1) and (2) are satisfied.
If y =
, and both equations (1) and (2) are satisfied.
If y = 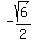 <---> x =
<---> x = 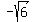 , and both equations (1) and (2) are satisfied.
2) 3x+y = 0 ====> y = -3x ====> substitute it into eq(1) ====>
, and both equations (1) and (2) are satisfied.
2) 3x+y = 0 ====> y = -3x ====> substitute it into eq(1) ====> 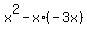 = 3 ====>
= 3 ====>  = 3
====>
= 3
====>  = 3/4 ====> x = +/-
= 3/4 ====> x = +/-  .
If x =
.
If x =  <---> y =
<---> y = 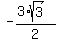 , and both equations (1) and (2) are satisfied.
If x =
, and both equations (1) and (2) are satisfied.
If x =  <---> y =
<---> y =  , and both equations (1) and (2) are satisfied.
Answer. The system (1), (2) has four solutions (x,y) = (
, and both equations (1) and (2) are satisfied.
Answer. The system (1), (2) has four solutions (x,y) = ( ,
,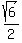 ), (
), (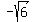 ,
,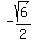 ), (
), ( ,
,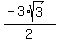 ), (
), ( ,
, ).
).