.
Let us do it step by step.
1.  =
= 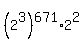 =
=  =
= 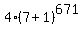 .
2.
.
2. 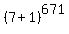 gives the remainder 1 when is divided by 7.
3. Therefore,
gives the remainder 1 when is divided by 7.
3. Therefore, 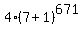 gives the remainder 4*1 = 4 when is divided by 7.
4. Thus, the first addend,
gives the remainder 4*1 = 4 when is divided by 7.
4. Thus, the first addend,  , gives the remainder 4 when is divided by 7.
5. 2015 gives the remainder 2 when is divided by 7.
So,
, gives the remainder 4 when is divided by 7.
5. 2015 gives the remainder 2 when is divided by 7.
So,  gives the remainder 2*2 = 4 when is divided by 7.
6. Finally, the sum
gives the remainder 2*2 = 4 when is divided by 7.
6. Finally, the sum 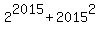 gives the remainder 4 + 4 = 8 when is divided by 7.
It is the same as to say that the sum
gives the remainder 4 + 4 = 8 when is divided by 7.
It is the same as to say that the sum 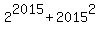 gives the remainder 1 when is divided by 7.
Answer. The remainder under the question is 1.
gives the remainder 1 when is divided by 7.
Answer. The remainder under the question is 1.