Question 1204411: What remainder is left when the number 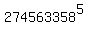 is divided by 9? is divided by 9?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hint: When dividing by 9, the remainder is equal to the sum of the digits.
Examples:
14/9 = 1 remainder 5, and 1+4 = 5
28/9 = 3 remainder 1, and 2+8 = 10 --> 1+0 = 1
45/9 = 5 remainder 0, and 4+5 = 9, getting remainder 9 is the same as remainder 0
127/9 = 14 remainder 1, and 1+2+7 = 10 --> 1+0 = 1
Notice how for some large sums, we have to add the digits up again.
This process is carried out until landing on a digit sum that is between 1 and 9.
If the digit sum is 9, then the original number is a multiple of 9.
This divisibility rule is very similar to the divisibility by 3 rule.
Another hint:
2+7+4+5+6+3+3+5+8 = 43 ---> 4+3 = 7
Therefore, 274563358/9 = some quotient remainder 7
We can then rephrase the problem as asking: What is the remainder of 7^5 when divided by 9?
One final hint: The powers of 7 mod 9 repeat themselves every three terms.
In other words,
7^1 = a (mod 9)
7^2 = b (mod 9)
7^3 = c (mod 9)
7^4 = a (mod 9)
and so on
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Use the rule of divisibility by 9:
The remainder of divisibility by 9 of the number N is the same,
as the remainder of the sum of digits of the number N when divided by 9.
The number 274563358 has the sum of its digits 2+7+4+5+6+3+3+5+8 = 43.
So, the number 274563358 itself, when divided by 9, gives the same remainder
as the sum of its digits 43 divided by 9, i.e. 43 mod 9 = 7.
Hence, 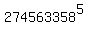 when divided by 9 gives the same remainder as the number when divided by 9 gives the same remainder as the number 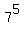 = 16807 when divided by 9.
Again, the number 16807 has the sum of the digits 1+6+8+7 = 22.
Therefore, the answer to the problem's question is 22 mod 9 = 4. = 16807 when divided by 9.
Again, the number 16807 has the sum of the digits 1+6+8+7 = 22.
Therefore, the answer to the problem's question is 22 mod 9 = 4.
Solved.
-----------------
On the rule of divisibility by 9 see the lessons
- Divisibility by 9 rule
- Restore the omitted digit in a number in a way that the number is divisible by 9
in this site.
|
|
|