Question 1025865: How many numbers from 1-1000 are there that are not divisible by any of the digits 2,3,5.
Found 2 solutions by ikleyn, KMST:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many numbers from 1-1000 are there that are not divisible by any of the  numbers 2,3,5. numbers 2,3,5.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
500 are divisible by 2 (set A).
333 are divisible by 3 (set B).
200 are divisible by 5 (set C).
166 are divisible by 6 = 2*3 (set AB, intersection of A and B).
100 are divisible by 10 = 2*5 (set AC, intersection of A and C).
66 are divisible by 15 = 3*5 (set BC, intersection of B and C).
33 are divisible by 30 = 2*3*5 (set ABC, intersection of A, B, and C).
Now, the number of integers from 1 to 1000 that are not divisible by any of the numbers 2,3,5, is
1000 - |A| - |B| - |C| + |AB| + |AC| + |BC| - |ABC|. (1)
It is equal to
1000 - 500 - 333 - 200 + 166 + 100 + 66 - 33 = 266.
And all that you (we, I) need is to prove the formula (1).
I will do it now.
Since we want to count those integer from 1 to 1000 that are not divisible by any of the numbers 2,3,5,
we exclude/distract the quantities of |A|, |B|, and |C| from 1000. (Step 1).
But doing this, we exclude/distract two times those integers that are in the intersections AB, AC and BC.
Therefore, we add these quantities in (1) for compensation. (Step 2).
In the step 1, we excluded/distracted 3 times the numbers of the set ABC.
In the step 2, we restored/added 3 times the numbers of the set ABC.
But we still need to exlude/distract the set ABC.
And we do it in the last term of the formula (1).
The formula (1) is proved, and the problem is solved.
Congratulations !!!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Among the numbers 1 - 1000 ,
 are divisible by are divisible by  ; ;
 are divisible by are divisible by  , ,
and since  , ,
 are divisible by are divisible by  . .
 are divisible by are divisible by  and and  ; ;
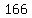 are divisible by are divisible by  and and 
(because  ), ),
and since  , ,
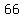 are divisible by are divisible by  and and  . .
Also, since  , ,
 of the numbers 1 - 1000 are divisible by of the numbers 1 - 1000 are divisible by  , ,  and and  . .
So the numbers from 1 through 100 that are not divisible by any of the digits 2, 3, and 5 are

|
|
|