 We see that when k=2
We see that when k=2
 And if we add any multiple of 11 to 2,
And if we add any multiple of 11 to 2,
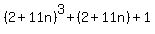 We get
We get
 which is
which is  plus some multiples of 11,
so integers of the form 2+11n, when n is a non-
negative integer, substituted for k into
plus some multiples of 11,
so integers of the form 2+11n, when n is a non-
negative integer, substituted for k into  will always yield a number divisible by 11.
They are the positive integers 2 mod 11.
Edwin
will always yield a number divisible by 11.
They are the positive integers 2 mod 11.
Edwin