SOLUTION: Use the perpendicular distance formula to determine how many times the line, 3x-5y+16=0 intersects the circle x^2+y^2=5. Thanks!!

Algebra ->  Coordinate-system -> SOLUTION: Use the perpendicular distance formula to determine how many times the line, 3x-5y+16=0 intersects the circle x^2+y^2=5. Thanks!!       Log On


   

Question 826151: Use the perpendicular distance formula to determine how many times the line, 3x-5y+16=0 intersects the circle x^2+y^2=5.
Thanks!!
Found 3 solutions by josgarithmetic, Alan3354, Jamie-L:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
I tried a bit of substitution, obtained a quadratic equation, for x as the single variable, and found an imaginary number result.

Very briefly, x%5E2%2B%28%283%2F5%29x%2B%2816%2F5%29%29%5E2=5 gave simplified 34x%5E2%2B96x%2B131=0; and discriminant is 96%5E2-4%2A34%2A131=-8600%3C0.

Best guess without trying to draw any graphs, no point of intersection.

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Use the perpendicular distance formula to determine how many times the line,
3x-5y+16=0 intersects the circle x^2+y^2=5.
----------------
The circle is centered at the Origin.
Find the distance from (0,0) to the line.
Slope of the line is 3/5
Slope perpendicular is -5/3
Line perpendicular is y = -5x/3
Intersection of the lines is:
3x-5y+16=0
3x + 25x/3 = -16
34x = -48
x = -24/17
---
y = 40/17
Distance from (0,0) to (-24/17,40/17) = 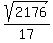sqrt%282176%29%2F17 =~ 2.744
Distance is > r --> no intersection

Answer by Jamie-L(5) About Me  (Show Source):
You can put this solution on YOUR website!
So basically you are trying to find the perpendicular distance (which is the same as the shortest distance) 3x-5y+16=0 is closest to the circle (or (0,0), since the centre of the circle is (0,0))
---------------------------------------------
By subbing the point (0,0) into the Perpendicular Distance Formula, you get:
---------------------------------------------
abs(3(0)-5(0)+16) / sqrt(3^2+5^2)
---------------------------------------------
which equals to 16/sqrt(34)
---------------------------------------------
The radius of the circle is root 5.
---------------------------------------------
16/sqrt(34) IS BIGGER than root 5. The line is further than the radius from the centre of the circle and therefore does not and cannot intersect the circle at any point.