Question 399366: In a triangle ABC, A (4 , 1), B (6 , 1) , C (4 , 6).
In a triangle A'B'C', A' (0 , -1), B' (-2 , -1), C' (0 , -6). Find the angle of rotation and centre of rotation.
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website! A (4 , 1), B (6 , 1) , C (4 , 6).
In a triangle A'B'C', A' (0 , -1), B' (-2 , -1), C' (0 , -6).
 Let's connect corresponding points:
Let's connect corresponding points:
 To find the center or rotation find the midpoint P of either
AA', BB', or CC'
If you find the midpoint of AA' using the formula
M = (
To find the center or rotation find the midpoint P of either
AA', BB', or CC'
If you find the midpoint of AA' using the formula
M = ( , , 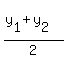 )
M = ( )
M = (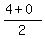 , , 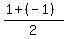 )
M = ( )
M = ( , , 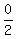 )
M = (2,0), that's the center of rotation.
It is not necessariy to do but one, but as a check,
If you find the midpoint of BB' using the formula
M = ( )
M = (2,0), that's the center of rotation.
It is not necessariy to do but one, but as a check,
If you find the midpoint of BB' using the formula
M = ( , , 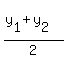 )
M = ( )
M = (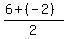 , , 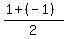 )
M = ( )
M = ( , , 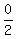 )
M = (2,0), that gives the same center of rotation.
and
If you find the midpoint of CC' using the formula
M = ( )
M = (2,0), that gives the same center of rotation.
and
If you find the midpoint of CC' using the formula
M = ( , , 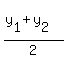 )
M = ( )
M = (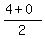 , , 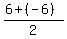 )
M = ( )
M = ( , , 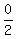 )
M = (2,0), which also gives the same center of rotation.
-------------------------------
The angle of rotation is 180°, because angles APA', BPB' and CPC'
are all straight angles, or 180°.
Edwin )
M = (2,0), which also gives the same center of rotation.
-------------------------------
The angle of rotation is 180°, because angles APA', BPB' and CPC'
are all straight angles, or 180°.
Edwin
|
|
|