Question 1147737: A is point (-1,6) on a cartesian graph, and B is point (14,9) on the same graph. Point C is on the x axis. What is the least value of AC+CB?
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
A is point (-1,6) on a cartesian   , and B is point (14,9) on the same .
Point C is on the x axis. What is the least value of AC+CB?
~~~~~~~~~~~~~~~~~
It follows the motives of well known (famous) minimization problem, solved about 400 years ago by Pierre Fermat.
The solution is as follows.
(1) Reflect the point A= (-1,6) about the x-axis as if x-axis is a mirror.
You will get the point A'= (-1,-6).
(2) Connect the points A'= (-1,-6) and the point B= (14,9) by a straight line.
It has the slope m =  =  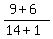= 1,
and its equation is y - (-6) = 1*(x - (-1)), which is the same as
y+6 = x+1, or y = x-5.
(3) Take the x-intercept of this line.
It is x= 5, y= 0, i.e. the point (5,0).
This point is what the problem asks for : C = (5,0).
The distance AC =  =  =  .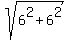
The distance BC =  =  =  .
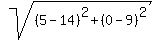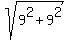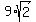ANSWER. The point C providing minimum sum of lengths AC + BC is C = (5,0).
The minimum value of AC + BC is + =  .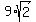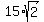
Solved.
|
|
|
