SOLUTION: Find the polar representation of [sin(a)+cos(a)] + i[sin(a)-cos(a)] Where "a" lies between 0 to 2<font face="symbol">p</font>.

[sin(a)+cos(a)] + i[sin(a)-cos(a)]

We use the facts that

1. cos(X)cos(Y)+cos(X)sin(Y) = cos(X-Y)
2. sin(X)cos(Y)-cos(X)sin(Y) = sin(X-Y)

and

3. sin() = cos() = 

Let's take the real part first:

sin(a)+cos(a), write it over 1,    

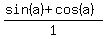Multiply it by  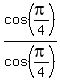which just equals 1
and therefore will not change the value:



 

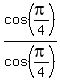
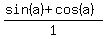
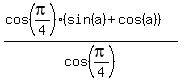Distribute on top 



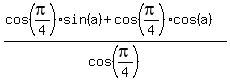By 3 above, replace the first cos() by sin()



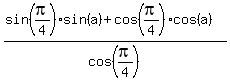Rearrange to look like cos(X)cos(Y)+cos(X)sin(Y) = cos(X-Y)

 

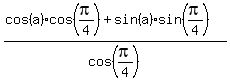So the numerator becomes cos(a-)

 

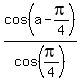Since the denominator  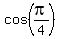= , we substitute 
and get:

 =  =  

------------------------------------

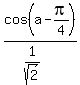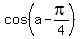
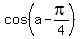
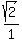
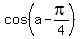Now we take the imaginary part, the coefficient of i:

sin(a)-cos(a), write it over 1,    

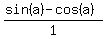Multiply it by  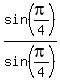which just equals 1
and therefore will not change the value:



 

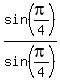
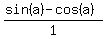
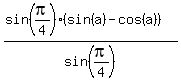Distribute on top 



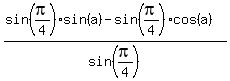By 3 above, replace the first sin() by cos()



Rearrange to look like sin(X)cos(Y)-cos(X)sin(Y) = sin(X-Y)

 

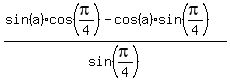So the numerator becomes sin(a-)

 

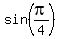Since the denominator  = , we substitute 
and get:

 =  =  

------------------------------------

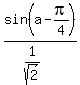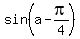
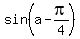
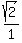
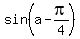So the original problem 

[sin(a)+cos(a)] + i[sin(a)-cos(a)]

becomes:

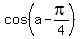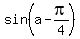
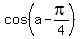 + i· 

[ + i·]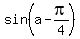 

That's the polar representation

which is often written as 

,

and electrical engineers

write it as ∠.  

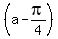 Edwin