How would I write the complex # y= -2+2i in trig form?
To draw the complex number 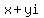 , plot the point
(x,y) and connect it to the origin (
, plot the point
(x,y) and connect it to the origin ( ,
, ).
So to draw the complex number
).
So to draw the complex number 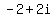 , we have
, we have  and
and  Now we plot the point (
Now we plot the point ( ,
, ) and connect it to
the origin (
) and connect it to
the origin ( ,
, ).
).
 now we draw a perpendicular down to the x-axis:
now we draw a perpendicular down to the x-axis:
 We label
We label  and
and 
 Now we calculate r by the Pythagorean equation:
Now we calculate r by the Pythagorean equation:






 So we label
So we label  as
as 
 Next we indicate the angle @ by a curved line:
Next we indicate the angle @ by a curved line:
 Now we determine the angle @ by any trig function
sin(@) =
Now we determine the angle @ by any trig function
sin(@) =  , cos(@) =
, cos(@) =  or tan(@) =
or tan(@) =  If we use the last one we have
tan(@) =
If we use the last one we have
tan(@) =  and since we know that 45° has tangent 1, we know
the reference angle is 45°, and since @ is in the
second quadrant, the actual angle is 180°-45°or 135°.
and since we know that 45° has tangent 1, we know
the reference angle is 45°, and since @ is in the
second quadrant, the actual angle is 180°-45°or 135°.
 The trig form is
r[cos(@) + i·sin(@)]
so we substitute and get:
The trig form is
r[cos(@) + i·sin(@)]
so we substitute and get:
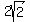 [cos(135°) + i·sin(135°)]
and sometimes this is abbreviated as
[cos(135°) + i·sin(135°)]
and sometimes this is abbreviated as
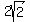 cis(135°)
Edwin
cis(135°)
Edwin