SOLUTION: find : 1/(2!) + 1/(3!) + 1/(4!) + ... + 1/(100!)

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: find : 1/(2!) + 1/(3!) + 1/(4!) + ... + 1/(100!)      Log On


   

Question 1208380: find : 1/(2!) + 1/(3!) + 1/(4!) + ... + 1/(100!)
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
find : 1/(2!) + 1/(3!) + 1/(4!) + ... + 1/(100!)
~~~~~~~~~~~~~~~~~~~~ 

Taylor series for e%5Ex is this convergent series

    e%5Ex = 1 + x%2F1%21 + x%5E2%2F2%21 + x%5E3%2F3%21 + . . . x%5En%2Fn%21 + 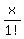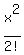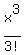. . .  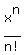   (1)


till infinity,  where  e = 2.71828...  is the base of natural logarithm.


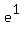So, e = e%5E1 = 1 + 1%2F1%21 + 1%2F2%21 + 1%2F3%21 + . . . 1%2Fn%21 + 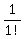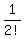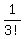. . .  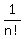   (2)


The given series is the series (2) for number "e" with the first two terms cut
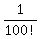and all the terms after  1%2F100%21  cut, but these later terms are so small 
that they can be neglected for reasonable precision.


Therefore, the given series is  e - 2 = 0.71828  (rounded).    ANSWER

Solved, with explanations.