Question 1208345: "In how many ways can the digits of the number 30348877 be arranged such that no two even digits are adjacent?"
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In how many ways can the digits of the number 30348877 be arranged such that
no two even digits are adjacent?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We have four even digits 0, 4, 8, 8 and 4 odd digits 3, 3, 7, 7.
Two possible placements are EOEOEOEO or OEOEOEOE, where E is the placeholder
for an even digit and O is the placeholder for an odd digit.
For odd digits with repetitions, as in the given number, there are
 = = 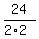 = 6 different distinguishable permutations are possible
inside the group of odd numbers.
For even digits with repetitions, as in the given number, there are = 6 different distinguishable permutations are possible
inside the group of odd numbers.
For even digits with repetitions, as in the given number, there are
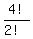 = =  = 12 different distinguishable permutations are possible
inside the group of even numbers.
Of these 12 arrangements, the number of those that start with 0 is 3; so these 3 should be subtracted from 12.
Doing this way, we find that the number of arrangements of four even numbers in this problems,
that do not start from 0 is 12-3 = 9.
Thus we have 6*12 = 72 arrangements of the type OEOEOEOE and 9*6 = 54 arrangements of the type EOEOEOEO.
The total is the sum 72 + 54 = 126.
Hence, in total, there are 126 different distinguishable arrangements as required in the problem. ANSWER = 12 different distinguishable permutations are possible
inside the group of even numbers.
Of these 12 arrangements, the number of those that start with 0 is 3; so these 3 should be subtracted from 12.
Doing this way, we find that the number of arrangements of four even numbers in this problems,
that do not start from 0 is 12-3 = 9.
Thus we have 6*12 = 72 arrangements of the type OEOEOEOE and 9*6 = 54 arrangements of the type EOEOEOEO.
The total is the sum 72 + 54 = 126.
Hence, in total, there are 126 different distinguishable arrangements as required in the problem. ANSWER
Solved.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are 8 digits of which 4 are even and 4 are odd. If no two even digits are adjacent, then the digits must alternate between even and odd.
I will use a different path to the answer than the other tutor. Maybe an easier path, maybe not; just different.
We can choose any of the 8 digits to be first. After that, since the even and odd digits must alternate, the numbers of choices for the subsequent digits are 4, 3, 3, 2, 2, 1, and 1. So the number of sequences in which we can choose the digits is 8*4*3*3*2*2*1*1.
But there are 3 pairs of identical digits. Because in each of those pairs the identical digits can be in either of 2 orders, this number of arrangements is too big by a factor of 2*2*2. So the number of ways of arranging the digits of the number is

ANSWER: 144
Note the other tutor doesn't allow 0 as a first digit. But the problem doesn't specifically preclude that; there are many applications where a "number" can have a leading 0.
If we don't allow 0 as the first digit, then the calculation shown above has 7 instead of 8 choices for the first digit, which leads to the answer of 126 obtained by the other tutor by her method.
|
|
|