Question 1208325: True or False: If S, P, and A are the cube roots of a complex number, then Arg(S)+Arg(P)=2×Arg(A).
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
True or False: If S, P, and A are the cube roots of a complex number, then Arg(S)+Arg(P)=2×Arg(A).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Mathematical symbol Arg (written with capital "A") is the principal value of the argument
of a complex number. In distinction from "arg" (written with lowercase "a"), Arg is always
in the interval [ , , ), while arg can differ from Arg by any integer multiple of ), while arg can differ from Arg by any integer multiple of  .
Let's consider first a simplest case of cube roots S, P and A of the number 1 (real one).
They have principal arguments 0, .
Let's consider first a simplest case of cube roots S, P and A of the number 1 (real one).
They have principal arguments 0,  and and 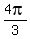 .
If to take these cube roots and their principal arguments in this order
s = 0, p = .
If to take these cube roots and their principal arguments in this order
s = 0, p =  , a = , a = 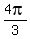 ,
where s = Arg(S), p = Arg(P), a = arg(A), then the equality s + p = 2a becomes 0 + ,
where s = Arg(S), p = Arg(P), a = arg(A), then the equality s + p = 2a becomes 0 +  = = 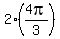 ,
which does not work (is FALSE). It works ONLY if we consider the equality by the modulo ,
which does not work (is FALSE). It works ONLY if we consider the equality by the modulo  .
If we take the roots and the sum of their principal arguments in other order, like s + a = 2p, we see that it works.
So, in order for the equality s + p = 2a be universal and work for any order of addends,
the formulation of the problem must be changed. The equality s + p = 2a should be considered by modulo .
If we take the roots and the sum of their principal arguments in other order, like s + a = 2p, we see that it works.
So, in order for the equality s + p = 2a be universal and work for any order of addends,
the formulation of the problem must be changed. The equality s + p = 2a should be considered by modulo  .
Then this modified statement will be true for any permutations (and for any order) of cube roots.
So, the correct formulation in this problem MUST BE
Arg(S) + Arg(P) = 2*Arg(A) (mod .
Then this modified statement will be true for any permutations (and for any order) of cube roots.
So, the correct formulation in this problem MUST BE
Arg(S) + Arg(P) = 2*Arg(A) (mod  ).
In this formulation, the statement of the problem is true independently of the order of addends.
For the proof in the general case, let S be the cube root of the complex number with the smallest principal argument s;
let P be the cube root of the complex number with the intermediate principal argument p;
and let A be the cube root of the complex number with the greatest principal argument "a".
Then, according to the de Moivre formula
p = s + ).
In this formulation, the statement of the problem is true independently of the order of addends.
For the proof in the general case, let S be the cube root of the complex number with the smallest principal argument s;
let P be the cube root of the complex number with the intermediate principal argument p;
and let A be the cube root of the complex number with the greatest principal argument "a".
Then, according to the de Moivre formula
p = s +  , a = s + , a = s + 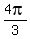 .
So , from one side, Arg(S) + Arg(P) = s + p = s + (s + .
So , from one side, Arg(S) + Arg(P) = s + p = s + (s + 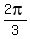 = 2s + = 2s +  ;
from the other side, 2*Arg(A) = 2*(s + ;
from the other side, 2*Arg(A) = 2*(s + 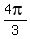 = 2s + = 2s + 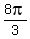 .
But .
But 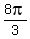 is the same as is the same as  modulo modulo  . Thus, we proved that
Arg(S) + Arg(P) = 2*Arg(A) (mod . Thus, we proved that
Arg(S) + Arg(P) = 2*Arg(A) (mod  ) (1)
in this order.
Furthermore, it is obvious, that equality (1) is valid for any permutation of the roots;
so, it is valid UNIVERSALLY for any order of the principal arguments.
At this point the proof and the solution are completed. ) (1)
in this order.
Furthermore, it is obvious, that equality (1) is valid for any permutation of the roots;
so, it is valid UNIVERSALLY for any order of the principal arguments.
At this point the proof and the solution are completed.
Solved.
But please note that it is valid universally ONLY for the modified formulation,
where the equality is by modulo  . .
Otherwise, it is EITHER invalid, OR is invalid as a universal equality for any/arbitrary order of the cube roots
(and, respectively, for any/arbitrary order of their principal arguments).
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: False
Explanation
Let's look at a counterexample. Consider the cube roots of 16.
We wish to solve z^3 = 16 or z^3-16 = 0.
According to the Nth Root Theorem we find the 3 cube roots are
S = 16^(1/3)*cis(0)
P = 16^(1/3)*cis(120)
A = 16^(1/3)*cis(240)
where cis(x) = cos(x)+i*sin(x) and the angle mode is in degrees.
If you want to convert to radians, then,
120 degrees = 2pi/3 radians
240 degrees = 4pi/3 radians
The order of the cube roots doesn't matter. Try out different permutations to see why.
Arg(S)+Arg(P) = 2*Arg(A)
0+120 = 2*240
120 = 480
Reaching a false statement proves that the original equation is false.
A bit of extra info:
Notice how angles 120 and 480 are coterminal. This is because 120+360=480.
If you were to involve mod 360 then the two sides would agree on the same number and the equation would be true.
To learn more, search "modular arithmetic".
|
|
|