Question 1208305: ((sin (x) + i cos (x)))^9 = sin (9 x) + i cos (9 x) , (true or false
Found 3 solutions by math_tutor2020, ikleyn, Edwin McCravy:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Answer: True
Work Shown
z = sin(x) + i*cos(x)
z = cos(90-x) + i*sin(90-x) ......... use trig identities
z^9 = cos(9*(90-x)) + i*sin(9*(90-x)) ................ De Moivre's Theorem
z^9 = cos(810 - 9x) + i*sin(810 - 9x)
z^9 = cos(810)cos(9x) + sin(810)sin(9x) + i*( sin(810)cos(9x) - cos(810)sin(9x) ) .... use two more trig identities
z^9 = 0*cos(9x) + 1*sin(9x) + i*( 1*cos(9x) - 0*sin(9x) )
z^9 = sin(9x) + i*cos(9x)
Answer by ikleyn(52786)  (Show Source):
You can put this solution on YOUR website! .
((sin(x) + i*cos(x)))^9 = sin(9x) + i*cos(9x), True or False.
~~~~~~~~~~~~~~~~~~~~~~~
It is a joke Math problem. I will show you a simple elegant solution,
also in a joking style. Consider it smiling.
sin(x) + i*cos(x) is not precisely a standard trigonometry form of a complex number.
As you know, a standard trigonometry form of a complex number is cos(x) + i*sin(x).
But we have what is given - therefore, I will apply a trick.
I will write sin(x) + i*cos(x) = i*(-i*sin(x) + cos(x)) = i*(cos(x) - i*sin(x)).
Now I will use the fact that cosine is an even function,
while sine is an odd function. Keeping it in mind, I can write
i*(cos(x) - i*sin(x)) = i*(cos(-x) + i*sin(-x)).
So, now in parentheses I have a standard trigonometry form of complex number
cos(-x) + i*sin(-x) for argument -x.
OK, very good. Now I raise sin(x) + i*cos(x), which is given to me,
to degree 9. Keeping in mind everything above, I have
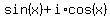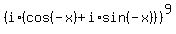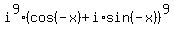 =  =  = i*(cos(-9x)+i*sin(-9x)). (1)
Here I used i^9 = i and de Moivre formula - standard facts from complex numbers.
Very good. Now I will use again that cosine is an even function,
while sine is an odd function. Keeping it in mind, I can write
i*(cos(-9x)+i*sin(-9x)) = i*(cos(9x) - i*sin(9x)). (2)
Last step is to open parentheses in the right side of this formula
i*(cos(9x) - i*sin(9x) = sin(9x) + i*cos(9x). (3)
Thus, combining formulas (1), (2) and (3), you get
 = sin(9x) + i*cos(9x).
It is what the problem asks to check.
The ANSWER to the problem's question is True.
At this point, the solution is complete.
----------------------------------------------------
As I said at the very beginning, this problem is a Math joke.
These tricks provide a complete elegant solution.
In a humorous way, if you turn a sock inside out twice,
it will return to its original form.
The meaning of this solution for you is to get understanding
that this problem is intended to be solved via these tricks with smiling.
It is a good problem for a teacher to show it to students at a Math circle.
First, the students will be shocked seeing these tricks.
Second, it will help them to master better manipulations with complex numbers.
Such problems and similar solutions have a great educational value.
If students will master them, they will teach next generations in the same way enthusiastically.
They are like a fuel for the engine of mathematical education, and they are real treasures.
Answer by Edwin McCravy(20056)  (Show Source):
|
|
|
