Question 1208303: let z = x + iy , | z^2 + 4| = |4 - 2 iz | , z ≠ 0 and Arg (- 3 z) = - 45 , then z = ....,
(2 - 2 i , 3 i - 3 , - 2 + 2 i ,3 - 3 i)
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Answer: -2+2i
--------------------------------------------------------------------------
Quick Explanation
Arg(kz) = Arg(z) + 180 when k < 0
Arg(-3z) = Arg(z) + 180
-45 = Arg(z) + 180
Arg(z) = -225 degrees which is coterminal to -225+360 = 135 degrees
Since Arg(z) = 135, this places the complex number in the northwest quadrant (i.e. upper left corner)
Of the four answer choices, only -2+2i is in this quadrant.
I'll let the student verify that z = -2+2i satisfies the equation abs(z^2+4) = abs(4-2iz)
abs(x) = absolute value of x
--------------------------------------------------------------------------
Longer Explanation
z = x+iy
w = -3+0i
Arg(z*w) = Arg(z)+Arg(w)
Arg(z*(-3)) = Arg(z)+Arg(-3)
Arg(z*(-3)) = Arg(z)+Arg(-3+0i)
Arg(-3z) = Arg(z)+180 degrees
Arg(-3z) = arctan(y/x)+180 degrees
Let's use the given info from the instructions.
Arg(-3z) = -45 degrees
arctan(y/x)+180 = -45
arctan(y/x) = -45-180
arctan(y/x) = -225
y/x = tan(-225)
y/x = -tan(225)
y/x = -1
y = -x
The complex number
z = x+iy
updates to
z = x+i(-x)
z = x-ix
Then,
z^2+4 = (x-ix)^2+4
z^2+4 = x^2-2ix^2+i^2x^2+4
z^2+4 = x^2-2ix^2+(-1)x^2+4
z^2+4 = x^2-2ix^2-x^2+4
z^2+4 = 4+(-2x^2)i
It has real part 4 and imaginary part -2x^2
abs(z^2+4) = magnitude of z^2+4 = absolute value of z^2+4
abs(z^2+4) = sqrt( realPart^2 + imaginaryPart^2 )
abs(z^2+4) = sqrt( 4^2 + (-2x^2)^2 )
abs(z^2+4) = sqrt( 4x^4+16 )
Let's refer to this as equation (1) so we can use it later.
4-2iz = 4-2i(x-ix)
4-2iz = 4-2ix+2i^2x
4-2iz = 4-2ix+2(-1)x
4-2iz = 4-2ix-2x
4-2iz = (4-2x)+(-2x)i
This has real part 4-2x and imaginary part -2x
abs(4-2iz) = sqrt( realPart^2 + imaginaryPart^2 )
abs(4-2iz) = sqrt( (4-2x)^2 + (-2x)^2 )
abs(4-2iz) = sqrt( 8x^2-16x+16 )
Let's refer to this as equation (2).
The instructions mention that the left hand sides of equations (1) and (2) are equal, so that allows us equate the right hand sides.
sqrt( 4x^4+16 ) = sqrt( 8x^2-16x+16 )
4x^4+16 = 8x^2-16x+16
4x^4-8x^2+16x+16-16 = 0
4x^4-8x^2+16x = 0
x(4x^3-8x+16) = 0
x = 0 or 4x^3-8x+16 = 0
If x = 0, then z = x-ix = 0-0i = 0, but we're specifically told in the instructions that z is nonzero.
We rule out x = 0 being allowed.
If you solve 4x^3-8x+16 = 0 through use of either- a graphing calculator
- the rational root theorem to generate the possible roots, then check each one
then you'll find that x = -2 is a root.
4x^3-8x+16 = 0
4(-2)^3-8(-2)+16 = 0
4(-8)+16+16 = 0
-32+16+16 = 0
0 = 0
Therefore
z = x-ix
becomes
z = -2-i(-2)
z = -2+2i
which is the final answer.
Note that Arg(-3z) = Arg(-3(-2+2i)) = Arg(6-6i) = -45 to help confirm the answer is correct.
I'll let the student verify the other requirement.
--------------------------------------------------------------------------
Extra info:
4x^3-8x+16 = 4(x+2)(x^2-2x+2)
You can use synthetic division to help factor.
Solving x^2-2x+2 = 0 leads to the complex roots x=1+i and x=1-i
Use the quadratic formula or complete the square.
If x=1+i, then,
z = x-ix
z = (1+i)-i(1+i)
z = (1+i)+(-i-i^2)
z = (1+i)+(-i-(-1))
z = (1+i)+(-i+1)
z = 2
But Arg(-3z) = Arg(-3*2) = Arg(-6+0i) = 180 when we wanted -45 instead.
The angles 180 and -45 are not coterminal.
This allows us to rule out x=1+i.
If x=1-i, then,
z = x-ix
z = (1-i)-i(1-i)
z = (1-i)+(-i+i^2)
z = (1-i)+(-i-1)
z = -2i
But Arg(-3z) = Arg(-3*(-2i)) = Arg(0+6i) = 90 instead of -45 degrees.
The angles 90 and -45 are not coterminal.
This allows us to rule out x=1-i.
Therefore, the only root we can use is x = -2.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
let z = x + iy , |z^2 + 4| = |4 - 2 iz|, z ≠ 0 and Arg(-3z) = -45 , then z = ....,
(A) 2 - 2i , (B) 3i - 3, (C) -2 + 2i, (D) 3 - 3i.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In his short solution, tutor @math_tutor2020 is not precisely correct.
He said that only one of four optional numbers is in the second quadrant.
It is not so. Together with -2+2i, the number 3i-3 is also in the second quadrant.
So, I came to bring another, really short, simple and complete solution.
First 4 lines of my solution repeat first 4 lines of the solution by @math_tutor2020.
But what follows after that, is different.
Arg(kz) = Arg(z) + 180 when k < 0
Arg(-3z) = Arg(z) + 180
-45 = Arg(z) + 180
Arg(z) = -225 degrees which is coterminal to -225+360 = 135 degrees.
Since Arg(z) = 135 degrees, complex number z is in the second quadrant and has the form
z = -a + ia, where "a" is a positive real number.
In the optional list, we have two and only two such numbers, (B) 3i-3, and (C) -2+2i.
So, we will consider two cases.
Case (C): z = -2+2i.
Then it is clear that z^2 will be pure imaginary. Indeed, z^2 = (-2+2i)^2 = 4 - 8i -4 = -8i.
Hence, z^2+4 = 4-8i and |4-8i| =  =  =  .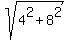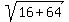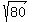
From the other side, 4-2iz = 4 - 2i*(-2+2i) = 4 + 4i + 4 = 8+4i.
Hence, |4-2iz| =  =  = .
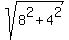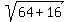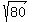Thus we see that |z^2+4| = |4-2iz|, so case (C) is the solution.
Case (B): z = 3i-3.
Again, it is clear that z^2 will be pure imaginary. Indeed, z^2 = (3i-3)^2 = -9 -18i + 9 = -18i.
Hence, z^2+4 = 4-18i and |4-18i| =  =  =  .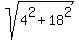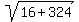
From the other side, 4-2iz = 4 - 2i*(3i-3) = 4 + 6 + 6i = 10+6i.
Hence, |4-2iz| =  =  =  .
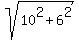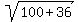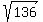Thus we see that |z^2+4| =/= |4-2iz|, so case (B) is not the solution.
Thus, from the four given options, only one, z = -2 + 2i, is the solution to the problem.
ANSWER. From the four given options, only one, z = -2 + 2i, is the solution to the problem.
Solved completely, in a short and simple way.
-------------------
I do not think that long solution by the other tutor is a right approach: it makes the entire job
unjustifiably long and complicated.
I also do not believe that this complicated way is the right way to teach.
And, finally, I do not think that that long complicated solution is what is expected.
The work can be done in much shorter and simpler way.
|
|
|
