SOLUTION: z = [1, theta ] , find (z + z ^(10))/(z - z ^(10)) by Polar form [ r , theta ],

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: z = [1, theta ] , find (z + z ^(10))/(z - z ^(10)) by Polar form [ r , theta ],      Log On


   

Question 1208302: z = [1, theta ] , find (z + z ^(10))/(z - z ^(10)) by Polar form [ r , theta ],
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
z = (1,theta), find (z + z^(10))/(z - z^(10)) highlight%28cross%28by%29%29 in polar form (r,theta).
~~~~~~~~~~~~~~~~~~~~~~ 

In cis-form,  z = cis%281%2Ctheta%29.   It means that the modulus of z is 1 and the argument of z is theta.

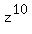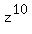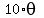Then  z%5E10 = cis%281%2C10%2Atheta%29.  In other words,  z%5E10 has the modulus 1  and the argument of  10%2Atheta.


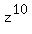To find the sum  z + z%5E10,  you should use the parallelogram rule of adding complex numbers as vectors.


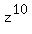Since both addends,  z  and  z%5E10  have equal modulus, the parallelogram rule in this case becomes
the rhombus rule.  In rhombus, the diagonal is the bisector of the angle.  
THEREFORE, in our case the argument of  z%2Bz%5E10  is

    %28theta%2B10%2Atheta%29%2F2%29 = 5.5%2Atheta%29. 


The modulus of  z%2Bz%5E10  is the third side of an isosceles triangle with the equal legs of the length 1 
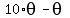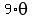and the angle between these legs of  10%2Atheta+-+theta = 9%2Atheta

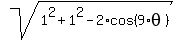    A = sqrt%281%5E2+%2B+1%5E2+-+2%2Acos%289%2Atheta%29%29 = sqrt%282-2cos%289%2Atheta%29%29.


So,  z+%2B+z%5E10 = cis%28A%2C5.5%2Atheta%29.



Similarly, for the denominator

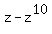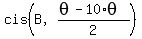    z+-+z%5E10 = cis%28B%2C%28theta-10%2Atheta%29%2F2%29 = cis%28B%2C-4.5%2Atheta%29%29,


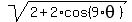where  B = sqrt%282%2B2%2Acos%289%2Atheta%29%29.   <<<---=== Note that the angle between  z  and  -z%5E10  is  
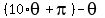                                             %2810%2Atheta%2Bpi%29-theta = 9%2Atheta%2Bpi

                                             and  cos%289%2Atheta%2Bpi%29 = -cos%289%2Atheta%29.


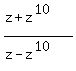Thus the ratio  %28z+%2B+z%5E%2810%29%29%2F%28z+-+z%5E%2810%29%29  has the modulus  

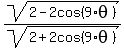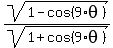    sqrt%282-2cos%289%2Atheta%29%29%2Fsqrt%282%2B2cos%289%2Atheta%29%29 = sqrt%281-cos%289%2Atheta%29%29%2Fsqrt%281%2Bcos%289%2Atheta%29%29   


and the argument as the difference

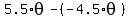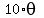    5.5%2Atheta+-+%28-4.5%2Atheta%29 = %285.5%2B4.5%29%2Atheta = 10%2Atheta.


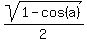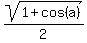Using formulas   sqrt%281-cos%28a%29%29%2F2 = sin%28a%2F2%29,  sqrt%281%2Bcos%28a%29%29%2F2 = cos%28a%2F2%29,  the modulus of the ratio can be simplified


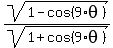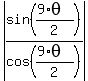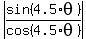    sqrt%281-cos%289%2Atheta%29%29%2Fsqrt%281%2Bcos%289%2Atheta%29%29  = abs%28sin%28%289%2Atheta%29%2F2%29%2Fcos%28%289%2Atheta%29%2F2%29%29 = abs%28sin%284.5%2Atheta%29%2Fcos%284.5%2Atheta%29%29



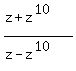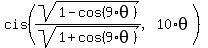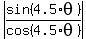Therefore, the ratio  %28z+%2B+z%5E%2810%29%29%2F%28z+-+z%5E%2810%29%29  is  cis%28sqrt%281-cos%289%2Atheta%29%29%2Fsqrt%281%2Bcos%289%2Atheta%29%29%2C10%2Atheta%29,  or, which is the same, (abs%28sin%284.5%2Atheta%29%2Fcos%284.5%2Atheta%29%29,10%2Atheta%29).


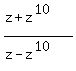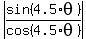ANSWER.  In polar form,  %28z+%2B+z%5E%2810%29%29%2F%28z+-+z%5E%2810%29%29  is   (abs%28sin%284.5%2Atheta%29%2Fcos%284.5%2Atheta%29%29,10%2Atheta%29).

Solved.


The key ideas of solution are

    - use cis-form of complex numbers;
    - use the parallelogram rule to add and to subtract complex numbers;
    - use the fact that the parallelogram rule in the case of equal modulus becomes the rhombus rule;
    - use the fact that in rhombus a diagonal bisects the angle of the rhombus
    - to find the modulus of the numerator and denominator, use the cosine law.

The rest is just arithmetic  (quite tight).


===========================


This problem is special. Its level is much higher than the average high school Math;
it is higher than teachers teach in Math schools, higher than average Math circles level,
different from regular Math Olympiads.

It is the level of Math Olympiads among undergraduate Math students of Math departments
of renowned universities/colleges, like the Putnam competition.

It does not require "flight of thought", but requires solid and firm knowledge of complex numbers
in all relevant aspects and firm knowledge of relevant adjacent Math subjects,
together with perfect and firm Math technique.