Question 1208298: if (x/y) + (y/x) = 1 , then y'' = (y/x) (True or False)
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
if (x/y) + (y/x) = 1 , then y'' = (y/x) (True or False)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let's investigate which (or what) function y(x) can be.
We have
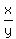 + +  = 1.
Let z = = 1.
Let z =  . Then . Then
 + z = 1,
1 + z^2 = z,
z^2 - z + 1 = 0, + z = 1,
1 + z^2 = z,
z^2 - z + 1 = 0,
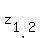 = = 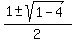 = = 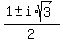 .
So, .
So,  has the constant value has the constant value  or or  . Hence,
y = z*x, where z is one of the two complex numbers z = . Hence,
y = z*x, where z is one of the two complex numbers z =  = = 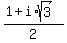 or z = or z =  = = 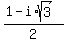 .
It implies
y' = z = const and then y'' = 0.
Thus we have to compare, from one side, y'' = 0 and, from the other side, .
It implies
y' = z = const and then y'' = 0.
Thus we have to compare, from one side, y'' = 0 and, from the other side,  = =  or or  , what are not zero.
So, the answer to the problem's question is , what are not zero.
So, the answer to the problem's question is  .
But an interesting fact, which is worth to be noticed, is that y' = z = .
But an interesting fact, which is worth to be noticed, is that y' = z =  has one of the two possible constant values has one of the two possible constant values
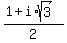 or or 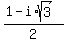 . .
Solved, answered and explained.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: False
If you said either y' = y/x or y'' = 0, then you would making a true statement.
Work Shown
w = x/y
w' = (y-x*y')/(y^2) .... quotient rule
z = y/x
z' = (y'*x-y)/(x^2) ... quotient rule
(x/y) + (y/x) = 1
w + z = 1
w' + z' = 0 ........ applied implicit derivative
(y-x*y')/(y^2) + (y'*x-y)/(x^2) = 0
( x^2(y-x*y') + y^2(y'*x-y) )/(x^2y^2) = 0
x^2(y-x*y') + y^2(y'*x-y) = 0
x^2*y-x^3*y' + xy^2*y'-y^3 = 0
-x^3*y'+xy^2*y' = -x^2*y+y^3
y'( -x^3+xy^2 ) = -x^2*y+y^3
y' = (-x^2*y+y^3)/(-x^3+xy^2)
y' = (-y(x^2-y^2))/(-x(x^2-y^2))
y' = y/x
Confirmation using WolframAlpha
https://www.wolframalpha.com/input?i=derivative+%28x%2Fy%29+%2B+%28y%2Fx%29+%3D+1
Another way to confirm is to use GeoGebra's ImplicitDerivative command.
https://geogebra.github.io/docs/manual/en/commands/ImplicitDerivative/
You would type in ImplicitDerivative(x/y+y/x-1) which produces the output y/x.
Then,
y' = y/x
y'' = (y'*x-y)/(x^2) .... quotient rule
y'' = ((y/x)*x-y)/(x^2) ....... substitute in y' = y/x
y'' = (y-y)/(x^2)
y'' = (0)/(x^2)
y'' = 0
--------------------------------------------------------------------------
Another Approach
(x/y) + (y/x) = 1
(x^2)/(xy)+(y^2)/(xy) = 1
(x^2+y^2)/(xy) = 1
Let
p = x^2+y^2
q = xy
Then
p' = 2x+2y*y'
q' = y+x*y'
So,
(x^2+y^2)/(xy) = 1
d/dx[ (x^2+y^2)/(xy) ] = d/dx[1]
d/dx[ p/q ] = 0
(p'*q - p*q')/(q^2) = 0 ............. quotient rule
p'*q - p*q' = 0
(2x+2y*y')xy - (x^2+y^2)(y+x*y') = 0
2x^2y+2xy^2*y' - (x^2(y+x*y')+y^2(y+x*y')) = 0
2x^2y+2xy^2*y' - (x^2y+x^3*y')-(y^3+xy^2*y') = 0
2x^2y+2xy^2*y' - x^2y-x^3*y'-y^3-xy^2*y' = 0
2xy^2*y'-x^3*y'-xy^2*y' = -2x^2y+x^2y+y^3
y'(2xy^2-x^3-xy^2) = -2x^2y+x^2y+y^3
y'(xy^2-x^3) = -x^2y+y^3
y' = (-x^2y+y^3)/(xy^2-x^3)
y' = (-y(x^2-y^2))/(-x(-y^2+x^2))
y' = (-y(x^2-y^2))/(-x(x^2-y^2))
y' = y/x
From here the steps are the same as the previous section.
|
|
|