SOLUTION: In what bases b, does (b+8) divide into (7b+8) with no remainder

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: In what bases b, does (b+8) divide into (7b+8) with no remainder      Log On


   

Question 1191126: In what bases b, does (b+8) divide into (7b+8) with no remainder
Found 2 solutions by Edwin McCravy, greenestamps:
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
Whether an integer divides into another integer with zero remainder has
nothing to do with what number base the integer is expressed in, so it's
as true in base ten as any other.
      
          7
 b+8) 7b+ 8
      7b+56
        -48 
        
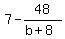7-48%2F%28b%2B8%29

This will only be a positive integer if 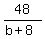48%2F%28b%2B8%29 is a positive
integer.  
   
The divisors of 48 are 1,2,4,6,8,12,16,24,48

b+8 =  1, 2, 4, 6,8,12,16,24,48
  b = -7,-6,-4,-2,0, 4, 8,16,40

The only valid values of b which can be number bases are the positive 
ones: 4, 8, 16, and 40.

Edwin

Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The statement of the problem is a bit awkward in using the term "bases". I interpret the problem to mean this:

For what values of b does (b+8) divide into (7b+8) with no remainder?

Going with that interpretation....

The requirement is that %287b%2B8%29%2F%28b%2B8%29 be an integer n.

Perform the "division" as quotient plus remainder:

n=%287b%2B8%29%2F%28b%2B8%29
n=%287b%2B56-48%29%2F%28b%2B8%29
n=%28%287b%2B56%29-48%29%2F%28b%2B8%29
n=%287b%2B56%29%2F%28b%2B8%29-48%2F%28b%2B8%29
n=7-48%2F%28b%2B8%29

In that last form of the equation, 7 is an integer, and we need n to be an integer; that means 48%2F%28b%2B8%29 has to be an integer.

So (b+8) has to be a factor of 48:
        b+8   48  24  16  12   8   6   4   3   2   1
          b   40  16   8   4   0  -2  -4  -5  -6  -7
    48/(b+8)   1   2   3   4   6   8  12  16  24  48
n=7-48/(b+8)   6   5   4   3   1  -1  -5  -9 -17 -41


The numbers in the second row of the table are all the integers for which (b+8) divides into (7b+8) with no remainder.

Examples....

b=16: b+8=24, 7b+8=112=8=120; 120/24=5

b=-4: b+8=4, 7b+8=-20; -20/4=-5

etc...