SOLUTION: If 1 and w are two of the five roots of w^5=1, then show that 1+w+w^2+w^3+w^4 = 0

There is an identity, which is valid for any real or complex number w

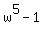     =       (1)


You may prove it directly, by making FOIL.

OR you may know it from the formula for the sum of a geometric progression.

In any way, I assume you know it.



Next step.  If w is the root of the equation 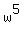  = 1, then the left side in (1) becomes equal to zero,
and you get

     = 0.     (2)


Since w is different from 1, the factor (w-1) is not zero, and you can cancel it in both sides of (2).

You will get then

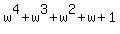     = 0,


exactly what should be proved.


Thus the proof is completed.

If w is the root of the equation w^5 = 1,  then 1, w, w^2, w^3, w^4 is the set of ALL 5 (five) roots of this equation.

    I proved it for you in my PREVIOUS post.


Now apply the Vieta's theorem: 


    for any polynomial equation of the degree n with the leading coefficient 1, 
    the sum of its roots is equal to the coef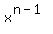ficient at  taken with the opposite sign.


Since in the given equation  x^5-1 = 0  the coefficient at    is 0 (zero, ZERO),
the sum of its roots is equal to zero:

    1 + w + w^2 + w^3 + w^4 = 0.


It is exactly what has to be proved.


The proof is completed.