Question 1152837: The points A, B represent complex number z1 and z2 respectively in the complex number plane, such that OAB is an equilateral tringle. O is the origin.
Prove that  . .
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Using trigonometric presentation of complex numbers (same as polar presentation),
I may assume that  = =  ,
where "r" is the modulus and ,
where "r" is the modulus and 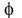 is the argument, i.e. the polar angle of the number is the argument, i.e. the polar angle of the number  .
Here I use the standard notation .
Here I use the standard notation 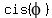 = = 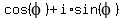 for complex numbers.
From the condition, for complex numbers.
From the condition,  = = 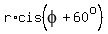 with the same modulus "r" and the argument with the same modulus "r" and the argument 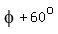 rotated by 60°.
Since the formula rotated by 60°.
Since the formula  = = 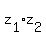 is uniform of the degree 2, the modules will cancel each other in both sides,
so I can forget about them and consider my complex numbers is uniform of the degree 2, the modules will cancel each other in both sides,
so I can forget about them and consider my complex numbers  and and  as the unit vectors beginning at 0 (zero point).
So, I need to prove that as the unit vectors beginning at 0 (zero point).
So, I need to prove that
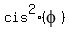 + + 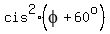 = = 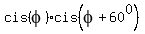 .
You remember that when complex numbers are multiplied, their arguments added.
Therefore, .
You remember that when complex numbers are multiplied, their arguments added.
Therefore, 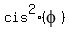 = = 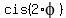 ; ; 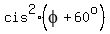 = = 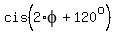 .
In other words, the angle between unit vectors .
In other words, the angle between unit vectors 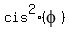 and and 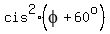 is 120°.
So, is 120°.
So, 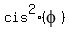 and and 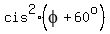 are the sides of the rhombus with the degree of 120° between them.
According to the "parallelogram rule" of adding complex numbers (and vectors),
the sum of the numbers are the sides of the rhombus with the degree of 120° between them.
According to the "parallelogram rule" of adding complex numbers (and vectors),
the sum of the numbers 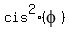 and and 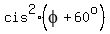 is the SHORT DIAGONAL of this rhombus,
i.e. the unit vector is the SHORT DIAGONAL of this rhombus,
i.e. the unit vector 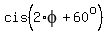 .
Thus I proved that .
Thus I proved that 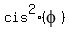 + + 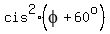 = = 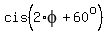 . (1)
From the other side, . (1)
From the other side, 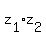 = = 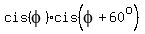 = = 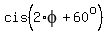 ,
i.e. the same complex number as (1).
Thus I proved that ,
i.e. the same complex number as (1).
Thus I proved that 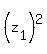 + + 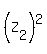 = = 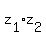 . .
C O M P L E T E D and S O L V E D.
On complex numbers, see introductory lessons
- Complex numbers and arithmetical operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Raising a complex number to an integer power
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Complex numbers".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|