Question 1118951: Solve each of the following quadratic equations using Quadratic Formula with answer in imaginary value.
1. 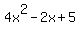
2. 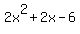
I got:
1. 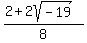 and and 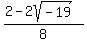
2. 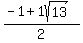 and and 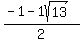
How do I proceed?
Found 2 solutions by Theo, solver91311:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! sqrt(-19) is equal to sqrt(19 * -1).
sqrt(-1) is equal to i.
therefore, sqrt(-19) is equal to i * sqrt(19).
this is equal to sqrt(-1) * sqrt(19) which is equal to sqrt(-19).
in place of sqrt(-19), use sqrt(19) * i
number 2 doesn't have an imaginary part since the number under your sqrt sign is positive.
your answer to 1 would be:
(2 + 2 * sqrt(19) * i) / 8 which your would simplify to .25 plus or minus 1.089724736 * i
that's what the quadratic equation solver i used got, so it looks good when you take into account rounding.
the quadratic equation solver i used got:
x = 0.25 + 1.0897247358852i or x = 0.25 - 1.0897247358852i
the quadratic solver gave me x = -2.302775637732 or x = 1.302775637732
your solution was x = (-1 plus or minus sqrt(13)) / 2.
this simplifies to x = -2.302775638 or x = 1.302775638.
same answer if you take into account rounding.
rules for imaginary numbers.
sqrt(-1) = i
sqrt(-1)^2 = -1
sqrt(-1)^3 = -i
sqrt(-1)^4 = 1
it repeats this for every sets of 4 exonents.
here's a reference.
https://www.mathsisfun.com/numbers/imaginary-numbers.html
the quadratic equation solver i used can be found at https://www.mathsisfun.com/quadratic-equation-solver.html
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let's begin with a quick review of terminology. The quadratic trinomials that you have listed are NOT quadratic equations. Equations have an equals sign somewhere in them; hence the name. Had you written:

(or with any other expression in the right-hand side), you would have been correct to call it a quadratic equation. For the time being, I'll simply assume that is what you meant (and probably what was written in your textbook, assignment sheet, test paper, or whatever).
Given that assumption, note the following:
(19)}\ =\ \sqrt{-1}\,\cdot\,\sqrt{19}\ =\ i\sqrt{19}) . .
Where  is the imaginary number defined by is the imaginary number defined by 
Then take the common factor of 2 out of the numerator and denominator:


As for the second problem, correcting the terminology error:

Your application of the quadratic formula, given that you actually had an equation to start with, is correct and reduced to lowest terms. Since the lead coefficient and the constant term have opposite signs, you are guaranteed to have two distinct real roots. ( must be non-negative and must be non-negative and  must be negative given opposite signs on must be negative given opposite signs on  and and  . Then, since you are subtracting the negative value . Then, since you are subtracting the negative value  , the entire result under the radical must be positive and therefore real. The consequence to this problem is that there is no imaginary part to the complex number representations of the two roots to the given equation. , the entire result under the radical must be positive and therefore real. The consequence to this problem is that there is no imaginary part to the complex number representations of the two roots to the given equation.
John

My calculator said it, I believe it, that settles it


|
|
|