SOLUTION: (z-1)/(z+1) = ki show |z| = 1

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: (z-1)/(z+1) = ki show |z| = 1       Log On


   

Question 1116382: (z-1)/(z+1) = ki
show |z| = 1
Answer by ikleyn(52824) About Me  (Show Source):
You can put this solution on YOUR website!
.
        Surely, the condition MUST be rewritten in this form 
          If 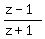%28z-1%29%2F%28z%2B1%29 = ki,   where k is a real number,  then show that |z| = 1.
        to be correct   (adding that k is a real number). 


Let  z = a + bi.

We are given 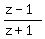 %28z-1%29%2F%28z%2B1%29 = ki,  which means that

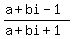%28a%2Bbi-1%29%2F%28a%2Bbi%2B1%29 = ki.


Left side is

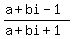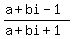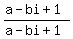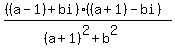%28a%2Bbi-1%29%2F%28a%2Bbi%2B1%29 = %28a%2Bbi-1%29%2F%28a%2Bbi%2B1%29.%28a-bi%2B1%29%2F%28a-bi%2B1%29 = %28%28%28a-1%29%2Bbi%29%2A%28%28a%2B1%29-bi%29%29%2F%28%28a%2B1%29%5E2%2Bb%5E2%29.


The denominator is now a real number.


The numerator is  (a-1)*(a+1) + bi*(a+1) - bi*(a-1) + b^2.


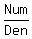Since the ratio  Num%2FDen is purely imaginary number ki,  it means that the real part of the numerator is zero:


    (a-1)*(a+1) + b^2 = 0,   or

    a^2 - 1 + b^2 = 0,  which is equivalent to

    a^2 + b^2 = 1.


    The last equality precisely means that  |z| = a^2 + b^2 = 1,   QED.

Solved.