Tutors Answer Your Questions about Complex Numbers (FREE)
Question 1210412: if limit e ^(x) sec (((b sin x))^2) = 0 as x \[LongRightArrow] - \[Infinity] , , then the possible values of b belong to the int erval ....
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! This problem is solved by analyzing the behavior of the two components of the function, $e^x$ and $\sec((b \sin x)^2)$, as $x \to -\infty$.
The limit is given as:
$$\lim_{x \to -\infty} e^x \sec((b \sin x)^2) = 0$$
### 1. Analyze the Exponential Term
As $x \to -\infty$, the term $e^x$ approaches **zero** very rapidly:
$$\lim_{x \to -\infty} e^x = 0$$
### 2. Analyze the Secant Term
The secant function is $\sec(\theta) = \frac{1}{\cos(\theta)}$. The argument is $\theta = (b \sin x)^2$.
* The term $\sin x$ is a bounded function: $-1 \le \sin x \le 1$.
* Therefore, the argument $\theta = (b \sin x)^2$ is also bounded: $0 \le (b \sin x)^2 \le b^2$.
The behavior of the limit is determined by whether the secant term is bounded, or whether it becomes unbounded (oscillating between $-\infty$ and $+\infty$).
$$\sec((b \sin x)^2) = \frac{1}{\cos((b \sin x)^2)}$$
For the limit of the product, $0 \times (\text{Term})$, to be $0$, the $(\text{Term})$ must be **bounded** or, at worst, approach a finite value.
If the secant term is **unbounded**, the limit would be of the indeterminate form $0 \times (\text{Unbounded})$, which may not be $0$. The secant term becomes unbounded (approaches $\pm \infty$) when its denominator, $\cos((b \sin x)^2)$, approaches $0$.
### 3. Determine the Condition for Boundedness
The secant function $\sec(\theta)$ is unbounded if its argument $\theta$ can take the form $\frac{\pi}{2} + n\pi$ for any integer $n$.
For $\sec((b \sin x)^2)$ to be **unbounded**, the value $(b \sin x)^2$ must pass through a singularity, i.e., satisfy:
$$(b \sin x)^2 = \frac{\pi}{2} + n\pi \quad \text{for some integer } n \ge 0$$
(Since the argument is a square, it must be non-negative, so $n$ starts at $0$).
For the secant term to be **bounded** for all $x$, its argument $(b \sin x)^2$ must *never* equal a singularity. Since $0 \le (b \sin x)^2 \le b^2$, we must ensure that the entire range of values $[0, b^2]$ does not contain any singularity.
The first singularity occurs at $\frac{\pi}{2}$.
The first two singularities are $\frac{\pi}{2}$ and $\frac{3\pi}{2}$.
For the secant term to be bounded, the maximum value of the argument, $b^2$, must be strictly less than the first singularity:
$$b^2 < \frac{\pi}{2}$$
If $b^2 < \frac{\pi}{2}$, then $\frac{1}{\cos((b \sin x)^2)}$ is a continuous function whose argument is always strictly between $0$ and $\frac{\pi}{2}$. Its value is therefore bounded between $\sec(0)=1$ and $\lim_{\theta \to (\pi/2)^-} \sec(\theta) = +\infty$, but the maximum value is $\sec(b^2)$, which is finite.
$$\lim_{x \to -\infty} \underbrace{e^x}_{\to 0} \underbrace{\sec((b \sin x)^2)}_{\text{Bounded}} = 0 \times (\text{Bounded}) = 0$$
### 4. Solve for $b$
We require:
$$b^2 < \frac{\pi}{2}$$
$$|b| < \sqrt{\frac{\pi}{2}}$$
$$-\sqrt{\frac{\pi}{2}} < b < \sqrt{\frac{\pi}{2}}$$
The possible values of $b$ belong to the interval:
$$\left(-\sqrt{\frac{\pi}{2}}, \sqrt{\frac{\pi}{2}}\right)$$
Question 1184007: prove by mathematical induction:
1^5 + 2^5 + 3^5 + ... + n^5 = (1/12)n^2(n+1)^2(2n^2 + 2n -1)
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Prove by induction that for all n >= 1
1^ 5 +2^ 5 +3^ 5 +^ ...+ n ^ 5 = [n ^ 2 * (n + 1) ^ 2 * (2n ^ 2 + 2n - 1)] / 12 .
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(a) The base of induction: n = 1.
Then the sum is one single term 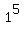 , which is 1.
The formula (*) at n = 1 gives , which is 1.
The formula (*) at n = 1 gives
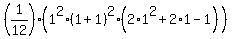 = = 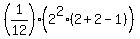 = = 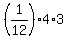 = = 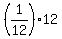 = 1,
so the base of induction is established.
(b) The step of induction.
We assume that for some integer k >= 1 this formula is valid
1^5 + 2^5 + 3^5 + . . . + k^5 = = 1,
so the base of induction is established.
(b) The step of induction.
We assume that for some integer k >= 1 this formula is valid
1^5 + 2^5 + 3^5 + . . . + k^5 = 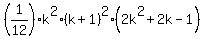 . (1)
We want to prove that then the formula is valid for the next integer number k+1, too:
1^5 + 2^5 + 3^5 + . . . + k^5 + (k+1)^5 = . (1)
We want to prove that then the formula is valid for the next integer number k+1, too:
1^5 + 2^5 + 3^5 + . . . + k^5 + (k+1)^5 =  . (2)
At this point, the proof of the formula (2) is started.
In the left side of (2), we replace the sum of the first k addends by the right side expression (1).
Thus we want to prove . (2)
At this point, the proof of the formula (2) is started.
In the left side of (2), we replace the sum of the first k addends by the right side expression (1).
Thus we want to prove
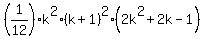 + + 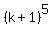 = =  . (3)
Let's transform left side of (3). We factor it, taking the common factor . (3)
Let's transform left side of (3). We factor it, taking the common factor 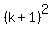 out of parentheses.
Then left side of (3) takes the form out of parentheses.
Then left side of (3) takes the form
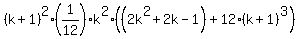 =
= =
= 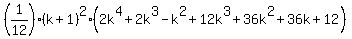 =
= =
= 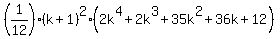 . (4)
Now, I used an online calculator to factor an expression in the internal parentheses,
and the calculator produced this decomposition . (4)
Now, I used an online calculator to factor an expression in the internal parentheses,
and the calculator produced this decomposition
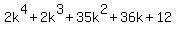 = = 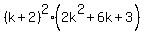 . (5)
( the link to the calculator is https://www.pocketmath.net , the mode is "Factor" ) )
This factorization can be continued this way . (5)
( the link to the calculator is https://www.pocketmath.net , the mode is "Factor" ) )
This factorization can be continued this way
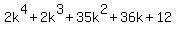 = = 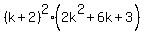 = = 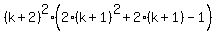 . (6)
Now, combining all pieces (4), (5) and (6) in one whole block, we have . (6)
Now, combining all pieces (4), (5) and (6) in one whole block, we have
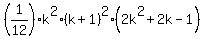 + + 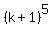 = =  . (7)
It is the same as (identical to) formula (3). Thus formula (3) is proven.
(3) Due to the principle of the mathematical induction, it means that formula . (7)
It is the same as (identical to) formula (3). Thus formula (3) is proven.
(3) Due to the principle of the mathematical induction, it means that formula
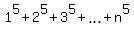 = = 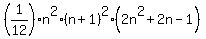 .
is proved for all integer n >= 1. .
is proved for all integer n >= 1.
Solved.
Question 1210411: Prove by induction that for all n >= 1
1^ 5 +2^ 5 +3^ 5 +^ ...+ n ^ 5 = [n ^ 2 * (n + 1) ^ 2 * (2n ^ 2 + 2n - 1)] / 12 .
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Prove by induction that for all n >= 1
1^ 5 +2^ 5 +3^ 5 +^ ...+ n ^ 5 = [n ^ 2 * (n + 1) ^ 2 * (2n ^ 2 + 2n - 1)] / 12 .
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(a) The base of induction: n = 1.
Then the sum is one single term 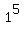 , which is 1.
The formula (*) at n = 1 gives , which is 1.
The formula (*) at n = 1 gives
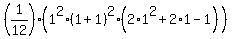 = = 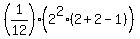 = = 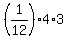 = = 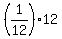 = 1,
so the base of induction is established.
(b) The step of induction.
We assume that for some integer k >= 1 this formula is valid
1^5 + 2^5 + 3^5 + . . . + k^5 = = 1,
so the base of induction is established.
(b) The step of induction.
We assume that for some integer k >= 1 this formula is valid
1^5 + 2^5 + 3^5 + . . . + k^5 = 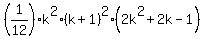 . (1)
We want to prove that then the formula is valid for the next integer number k+1, too:
1^5 + 2^5 + 3^5 + . . . + k^5 + (k+1)^5 = . (1)
We want to prove that then the formula is valid for the next integer number k+1, too:
1^5 + 2^5 + 3^5 + . . . + k^5 + (k+1)^5 =  . (2)
At this point, the proof of the formula (2) is started.
In the left side of (2), we replace the sum of the first k addends by the right side expression (1).
Thus we want to prove . (2)
At this point, the proof of the formula (2) is started.
In the left side of (2), we replace the sum of the first k addends by the right side expression (1).
Thus we want to prove
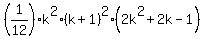 + + 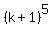 = =  . (3)
Let's transform left side of (3). We factor it, taking the common factor . (3)
Let's transform left side of (3). We factor it, taking the common factor 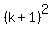 out of parentheses.
Then left side of (3) takes the form out of parentheses.
Then left side of (3) takes the form
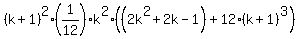 =
= =
= 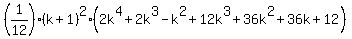 =
= =
= 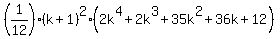 . (4)
Now, I used an online calculator to factor an expression in the internal parentheses,
and the calculator produced this decomposition . (4)
Now, I used an online calculator to factor an expression in the internal parentheses,
and the calculator produced this decomposition
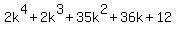 = = 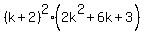 . (5)
( the link to the calculator is https://www.pocketmath.net , the mode is "Factor" ) )
This factorization can be continued this way . (5)
( the link to the calculator is https://www.pocketmath.net , the mode is "Factor" ) )
This factorization can be continued this way
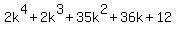 = = 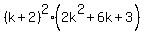 = = 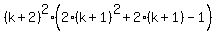 . (6)
Now, combining all pieces (4), (5) and (6) in one whole block, we have . (6)
Now, combining all pieces (4), (5) and (6) in one whole block, we have
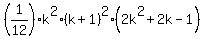 + + 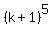 = =  . (7)
It is the same as (identical to) formula (3). Thus formula (3) is proven.
(3) Due to the principle of the mathematical induction, it means that formula . (7)
It is the same as (identical to) formula (3). Thus formula (3) is proven.
(3) Due to the principle of the mathematical induction, it means that formula
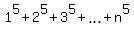 = = 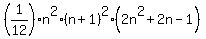 .
is proved for all integer n >= 1. .
is proved for all integer n >= 1.
Solved.
Question 1210398: Let f(x)= 1/(x+1). Determine the derivative of the -th iterate of , that is, compute , where denotes the composition of with itself times."
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
See nice solution produced by Artificial Intelligence at this link
https://www.google.com/search?q=Let+f(x)%3D+1%2F(x%2B1).+Determine+the+derivative+of+the+-th+iterate+of+%2C+that+is%2C+compute+%2C+where+denotes+the+composition+of+with+itself+times.%22&rlz=1C1CHBF_enUS1071US1071&oq=Let+f(x)%3D+1%2F(x%2B1).+Determine+the+derivative+of+the+-th+iterate+of+%2C+that+is%2C+compute+%2C+where+denotes+the+composition+of+with+itself+times.%22&gs_lcrp=EgZjaHJvbWUyBggAEEUYOTIHCAEQIRiPAjIHCAIQIRiPAtIBCTIwOTFqMGoxNagCCLACAfEFH9zaLFZD0wI&sourceid=chrome&ie=UTF-8
(first output under this link).
Question 1210400: Let f(x)= 1/(x+1).
Determine the derivative of the -th iterate of , that is, compute , where denotes the composition of with itself times."
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
See nice solution produced by Artificial Intelligence at this link
https://www.google.com/search?q=Let+f(x)%3D+1%2F(x%2B1).+Determine+the+derivative+of+the+-th+iterate+of+%2C+that+is%2C+compute+%2C+where+denotes+the+composition+of+with+itself+times.%22&rlz=1C1CHBF_enUS1071US1071&oq=Let+f(x)%3D+1%2F(x%2B1).+Determine+the+derivative+of+the+-th+iterate+of+%2C+that+is%2C+compute+%2C+where+denotes+the+composition+of+with+itself+times.%22&gs_lcrp=EgZjaHJvbWUyBggAEEUYOTIHCAEQIRiPAjIHCAIQIRiPAtIBCTIwOTFqMGoxNagCCLACAfEFH9zaLFZD0wI&sourceid=chrome&ie=UTF-8
(first output under this link).
Question 1210389: The function f(x) = (1\x) is decreasing on its domain ( true or false)
Found 3 solutions by math_tutor2020, ikleyn, josgarithmetic:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: true
Explanation
I think you meant to type
f(x) = 1/x
As x gets bigger, i.e. as we move to the right, what happens to y = 1/x?
We can look at a graph to note how it goes downhill throughout its entire domain.
Therefore the answer is true

As x gets bigger, y gets smaller.
As we move to the right the curve goes downhill.
A way to do this without a graph is to plug in a value like x = 2
1/x = 1/2 = 0.50
Then plug in x = 3
1/x = 1/3 = 0.33 approximately
Comparing 0.50 with 0.33 shows that y has gone down, which helps show the function decreases.
Keep in mind that this does not prove it always decreases over the entire domain.
You'll have to use the method mentioned in the next paragraph.
Let's do a formal proof.
Let a > 0 and b > 0.
Since both are positive this means a+b > 0.
Plug in x = a to arrive at 1/a which is also positive.
Plug in x = a+b to arrive at 1/(a+b) which is also positive.
Now to compare 1/a with 1/(a+b)
Assume for now they are equal,
1/a = 1/(a+b)
a+b = a .... cross multiply
b = 0
We arrive at a contradiction since we made b > 0 earlier.
To fix those errors, replace each equal sign with a greater than sign
1/a > 1/(a+b)
a+b > a .... cross multiply
b > 0
Or basically we move through those steps backwards like so
b > 0
a+b > a
1/a > 1/(a+b)
This basically shows that for some input x = a, if we nudge that input to the right a bit to arrive at x = a+b, then we have shown that 1/a is larger than 1/(a+b)
In short we have proven the function is always going downhill no matter where you're on it.
Note that we can follow very similar steps when a < 0 and b > 0, to effectively mirror things over the y axis.
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The function f(x) = (1\x) is decreasing on its domain ( true or false)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
First of all, I read this function as f(x) = 1/x,
following to the standard rules commonly accepted in Math.
The domain is the set of all real numbers except of 0 (zero).
Function f(x) = 1/x has two branches: one over the set of positive 'x',
another over the set of negative 'x'.
For each branch separately, function f(x) = 1/x is monotonic in each sub-domain.
Or, more accurately, function f(x) = 1/x is monotonically decreases locally in each sib-domain.
To prove it, take the derivative: it is - 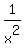 . .
The denominator  is always positive for all 'x' of the domain; so, the derivative is always negative. is always positive for all 'x' of the domain; so, the derivative is always negative.
You also can convince yourself by making a plot of this function.
For it, go to website https:\\www.desmos.com/calculator/
Print the formula for the function y = 1/x.
You will get the plot instantly.
The plot clearly shows that the function monotonically decreases as 'x' increases in the domain.
So, locally for each branch, the function f(x) = 1/x monotonically decreases.
You have this answer proved formally and demonstrated / illustrated visually.
But we can not say that function f(x) = 1/x is globally decreasing: when 'x' moves
from negative values to positive values, the function 1/x jumps from negative values to positive,
breaking monotonicity.
So, locally this function is monotonically decreasing, but globally it is not monotonic.
//////////////////////////////////////
This problem is an elementary  . .
As I explained in my post above, locally and piece-wisely, the function is monotonically decreasing.
But globally, it is NOT monotonic.
It is OBVIOUS: compare these values of the function
x -2 -1 1 2
1/x -0.5 -1 1 0.5
decrease decrease
increase
They show non-monotonic behavior.
Tutor @math_tutor2000 fell into this trap.
Answer by josgarithmetic(39629)  (Show Source): (Show Source):
Question 1210388: The function f(x) = (1\x) is monotonic on its domain ( true or false) ?
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The function f(x) = (1\x) is monotonic on its domain ( true or false) ?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
First of all, I read this function as f(x) = 1/x,
following to the standard rules commonly accepted in Math.
The domain is the set of all real numbers except of 0 (zero).
Function f(x) = 1/x has two branches: one over the set of positive 'x',
another over the set of negative 'x'.
For each branch separately, function f(x) = 1/x is monotonic in each sub-domain.
Or, more accurately, function f(x) = 1/x is monotonically decreases locally in each sib-domain.
To prove it, take the derivative: it is - 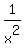 . .
The denominator  is always positive for all 'x' of the domain; so, the derivative is always negative. is always positive for all 'x' of the domain; so, the derivative is always negative.
You also can convince yourself by making a plot of this function.
For it, go to website https:\\www.desmos.com/calculator/
Print the formula for the function y = 1/x.
You will get the plot instantly.
The plot clearly shows that the function monotonically decreases as 'x' increases in the domain.
So, locally for each branch, the function f(x) = 1/x monotonically decreases.
You have this answer proved formally and demonstrated / illustrated visually.
But we can not say that function f(x) = 1/x is globally decreasing: when 'x' moves
from negative values to positive values, the function 1/x jumps from negative values to positive,
breaking monotonicity.
So, locally this function is monotonically decreasing, but globally it is not monotonic.
/////////////////////////////////
After reading the post by @math_tutor2020
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1210389.html
This problem is an elementary  . .
As I explained, locally and piece-wisely, the function is monotonically decreasing.
But globally, it is NOT monotonic.
It is OBVIOUS: compare these values
x -2 -1 1 2
1/x -0.5 -1 1 0.5
decease decrease
increase
They show non-monotonic behavior.
Tutor @math_tutor2000 fell into this trap.
Question 1210380: Solve the equation [x² + 2x + 5] - [x + 1] = 6, where the symbol [ ] denotes the greatest integer function (floor function).
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve the equation [x² + 2x + 5] - [x + 1] = 6, where the symbol [ ] denotes
the greatest integer function (floor function).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For clarity, I will write this equation in this form
floor(x^2 + 2x + 5) - floor(x+1) = 6. (1)
I will solve it step by step.
(1) x^2 + 2x + 5 = (x+1)^2 + 4.
Therefore, floor(x^2 + 2x + 5) = floor((x+1)^2 + 4).
Next, it is clear that floor((x+1)^2+4) = floor((x+1)^2) + 4.
Therefore, equation (1) is equivalent to
floor((x+1)^2) + 4 - floor(x+1) = 6,
or
floor((x+1)^2 - floor(x+1) = 2.
(2) Now I will introduce new variable u = x+1 to simplify writing.
So, now an equation to solve is
floor(u^2) - floor(u) = 2. (2)
(3) For what will follow, it is convenient to look at the plot of the functions
u --> y = floor(u^2) - floor(u) and y = 2.
These functions are shown in the plot https://www.desmos.com/calculator/9eg9wmaonb
(4) In the interval -1 < u < 0, floor(u^2) = 0 and floor(u) = -1, so floor(u^2) - floor(u) = 0 - (-1) = 1,
which means that there are no solutions to equation (2) in this interval.
(5) At point u = -1, floor(u^2) = 1; floor(u) = -1, so floor(u^2) - floor(u) = 1 - (-1) = 2,
which means that u = -1 is a solution to equation (2).
(5) In the interval -2 < u < -1, floor(u^2) has values 1 or 2 or 3; floor(u) = -2,
so floor(u^2) - floor(u) has values 3, or 4, or 5,
which means that there are no solutions to equation (2) in this interval.
At this point, it is clear that there is no sense to analyze further
for negative 'u' lesser than -2, because there are no solutions to equation (2) there.
(6) In the interval 0 < u < 1, floor(u^2) has value 0; floor(u) has value 0, so floor(u^2) - floor(u) = 0 - 0 = 0,
which means that there are no solutions to equation (2) in this interval.
(7) At point u = 1, floor(u^2) = 1; floor(u) = 1, so floor(u^2) - floor(u) = 1 - 1 = 0,
which means that u = 1 is not a solution to equation (2).
(8) In the interval 1 < u <  , floor(u^2) has value1 1; floor(u) = 1,
so floor(u^2) - floor(u) = 1 - 1 = 0,
which means that there are no solutions to equation (2) in this interval.
(9) At point u = , floor(u^2) has value1 1; floor(u) = 1,
so floor(u^2) - floor(u) = 1 - 1 = 0,
which means that there are no solutions to equation (2) in this interval.
(9) At point u =  , floor(u^2) = 2; floor(u) = 1, so floor(u^2) - floor(u) = 2 - 1 = 1,
which means that u = , floor(u^2) = 2; floor(u) = 1, so floor(u^2) - floor(u) = 2 - 1 = 1,
which means that u =  is not a solution to equation (2).
(10) In the interval is not a solution to equation (2).
(10) In the interval  < u < < u <  , floor(u^2) has value 2; floor(u) = 1,
so floor(u^2) - floor(u) = 2 - 1 = 1,
which means that there are no solutions to equation (2) in this interval.
(11) At point u = , floor(u^2) has value 2; floor(u) = 1,
so floor(u^2) - floor(u) = 2 - 1 = 1,
which means that there are no solutions to equation (2) in this interval.
(11) At point u =  , floor(u^2) = 3; floor(u) = 1, so floor(u^2) - floor(u) = 3 - 1 = 2,
which means that u = , floor(u^2) = 3; floor(u) = 1, so floor(u^2) - floor(u) = 3 - 1 = 2,
which means that u =  is a solution to equation (2).
(12) In the interval is a solution to equation (2).
(12) In the interval  <= u < 2, floor(u^2) has value 3; floor(u) = 1,
so floor(u^2) - floor(u) = 3 - 1 = 2,
which means that all this interval is the solution to equation (2).
(13) At point u = 2, floor(u^2) = 4; floor(u) = 2, so floor(u^2) - floor(u) = 4 - 2 = 2,
which means that u = 2 is a solution to equation (2).
(14) In the interval 2 < u < <= u < 2, floor(u^2) has value 3; floor(u) = 1,
so floor(u^2) - floor(u) = 3 - 1 = 2,
which means that all this interval is the solution to equation (2).
(13) At point u = 2, floor(u^2) = 4; floor(u) = 2, so floor(u^2) - floor(u) = 4 - 2 = 2,
which means that u = 2 is a solution to equation (2).
(14) In the interval 2 < u <  , floor(u^2) has value 4; floor(u) = 2,
so floor(u^2) - floor(u) = 4 - 2 = 2,
which means that all this interval is the solution to equation (2).
(15) At point u = , floor(u^2) has value 4; floor(u) = 2,
so floor(u^2) - floor(u) = 4 - 2 = 2,
which means that all this interval is the solution to equation (2).
(15) At point u =  , floor(u^2) = 5; floor(u) = 2, so floor(u^2) - floor(u) = 5 - 2 = 3,
which means that u = , floor(u^2) = 5; floor(u) = 2, so floor(u^2) - floor(u) = 5 - 2 = 3,
which means that u =  is not a solution to equation (2).
At this point, it is clear that there is no sense to analyze further
for positive 'u' greater than is not a solution to equation (2).
At this point, it is clear that there is no sense to analyze further
for positive 'u' greater than  , because there are no solutions to equation (2) there.
At this point, we can summarize the solution set for variable u: it is the union of sets of real numbers
< -1 > U [ , because there are no solutions to equation (2) there.
At this point, we can summarize the solution set for variable u: it is the union of sets of real numbers
< -1 > U [  <= u < <= u <  ).
Now we can return to variable x and to describe the solution set for the given equation (1) in terms of x. It is
< -2 > U [ ).
Now we can return to variable x and to describe the solution set for the given equation (1) in terms of x. It is
< -2 > U [  <= x < <= x <  ). <<<---=== ANSWER ). <<<---=== ANSWER
Thus the problem is solved completely.
/////////////////////////////////////////////////////
What to do if in the future you will get a similar problem ?
First, make a plot using an advanced computer plotting tool like DESMOS:
it will tell you a lot about the possible solution.
Then start analyze, and pay a special attention analyzing all possible relevant intervals
and all possible points of discontinuity of the floor function at every term in the equation.
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
The Google AI solution for this problem under the link
https://www.google.com/search?q=Solve+the+equation+%5Bx%C2%B2+%2B+2x+%2B+5%5D+-+%5Bx+%2B+1%5D+%3D+6%2C+where+the+symbol+%5B+%5D+denotes+the+greatest+integer+function+(floor+function).&rlz=1C1CHBF_enUS1071US1071&oq=Solve+the+equation+%5Bx%C2%B2+%2B+2x+%2B+5%5D+-+%5Bx+%2B+1%5D+%3D+6%2C+where+the+symbol+%5B+%5D+denotes+the+greatest+integer+function+(floor+function).&gs_lcrp=EgZjaHJvbWUyBggAEEUYOTIGCAEQRRg9MgYIAhBFGDzSAQkyNDU4ajBqMTWoAgiwAgHxBc1B77cLzH-J&sourceid=chrome&ie=UTF-8
of today, 8/19/2025, misses the value x = -2, which satisfies the given equation --- so, their answer and their analysis are INCOMPLETE.
I reported to them about this default via their feedback system.
Question 1210376: find the domain and range of f(x) = (x)/(sqrt(1 - ((sqrt(- x)))^2))
Found 2 solutions by Edwin McCravy, mccravyedwin:
Answer by Edwin McCravy(20063)   (Show Source): (Show Source):
Answer by mccravyedwin(408)   (Show Source): (Show Source):
Question 1210374: let x , y \[Element] R , prove that , 1) | x + y | = | x | + | y | \[DoubleLeftRightArrow] x . y \[GreaterEqual] 0, 2) | x - y | = | x | - | y | \[DoubleLeftRightArrow] (x - y) y \[GreaterEqual] 0, 3) | x - y | = | x | + | y | \[DoubleLeftRightArrow] x . y \[GreaterEqual] 0
Answer by ikleyn(52875)   (Show Source): (Show Source):
Question 1210370: Using the discriminant method, find the range of the function:
y =(x+1)/(sqrt(x² - 5))
Found 2 solutions by ikleyn, mccravyedwin:
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Using the discriminant method, find the range of the function:
y = (x+1)/(sqrt(x² - 5))
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will solve this problem and will find the range of the given function algebraically,
using the discriminant method.
But for better understanding, I will start from the plot, which I prepared using
the plotting tool DESMOS. This plotting tool is free of charge at this website
http://desmos.com/calculator/
The link to my plot is this https://www.desmos.com/calculator/lhfouvblry
Looking at the function and at the plot, we see that the domain of the function is
x^2-5 > 0, or x <  U x > U x >  (the union of two sets).
In the area x > (the union of two sets).
In the area x >  , when x approaches to , when x approaches to  from the right side, the function
asymptotically goes to infinity.
In the same area, x > from the right side, the function
asymptotically goes to infinity.
In the same area, x >  , when x goes to positive infinity, the function is asymptotically
close to , when x goes to positive infinity, the function is asymptotically
close to 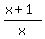 , so, it goes to 1 unit monotonically decreasing.
Hence, the range of the right branch of the function at positive x > , so, it goes to 1 unit monotonically decreasing.
Hence, the range of the right branch of the function at positive x >  is from 1 to infinity,
or ( is from 1 to infinity,
or (  , , ).
In the area x < ).
In the area x <  , when x approaches to , when x approaches to  from the left side, the function
asymptotically goes to negative infinity.
In the same area, x < from the left side, the function
asymptotically goes to negative infinity.
In the same area, x <  , when x goes to negative infinity, the function is asymptotically
close to , when x goes to negative infinity, the function is asymptotically
close to 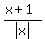 , so, it goes to negative 1 unit, or (-1), monotonically decreasing.
But at x = -3, the value of the function is (-1), as it is easy to check, and then, in the area , so, it goes to negative 1 unit, or (-1), monotonically decreasing.
But at x = -3, the value of the function is (-1), as it is easy to check, and then, in the area
 < x < 3, the function is greater than -1 and tends to -1 from greater values than -1.
Hence, the function has a local maximum somewhere between -3 and < x < 3, the function is greater than -1 and tends to -1 from greater values than -1.
Hence, the function has a local maximum somewhere between -3 and  .
+------------------------------------------------------------------------+
| The major goal of this problem is to determine this local maximum. |
| As we get this local maximum, we will solve the problem completely. |
+----------------------------------------------------------------------=-+
OK. The next part of the solution is the .
+------------------------------------------------------------------------+
| The major goal of this problem is to determine this local maximum. |
| As we get this local maximum, we will solve the problem completely. |
+----------------------------------------------------------------------=-+
OK. The next part of the solution is the  . Let's write . Let's write
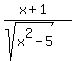 = t, (1)
by introducing new variable 't'.
We want to find maximum value of 't' in the area = t, (1)
by introducing new variable 't'.
We want to find maximum value of 't' in the area  < x < < x <  .
From equation (1), we have
(x+1)^2 = t^2*(x^2-5),
x^2 + 2x + 1 = t^2*x^2 - 5t^2,
(t^2-1)x^2 - 2x - (5t^2+1) = 0. (2)
+---------------------------------------------------------------------+
| The discriminant principle says that the extremal value of 't' |
| in this equation is achieved when the discriminant |
| of this equation is zero. |
| It is the condition that equation (2) has emerging roots in x. |
+---------------------------------------------------------------------+
So, the discriminant of equation (2) is
d = b^2 - 4ac = (-2)^2 + 4*(t^2-1)*((5t^2+1) = 4 + 4(t^2-1)*(5t^2+1).
The equation d = 0 is then
4 + 4(t^2-1)*(5t^2+1) = 0,
or
(t^2-1)*(5t^2+1) = -1. (3)
For simplicity, let's introduce new variable u = t^2.
Then equation (3) takes the form
(u-1)*(5u+1) = -1,
5u^2 - 4u - 1 = -1,
5u^2 - 4u = 0,
u*(5u - 4) = 0.
It has the roots u = 0 and u = .
From equation (1), we have
(x+1)^2 = t^2*(x^2-5),
x^2 + 2x + 1 = t^2*x^2 - 5t^2,
(t^2-1)x^2 - 2x - (5t^2+1) = 0. (2)
+---------------------------------------------------------------------+
| The discriminant principle says that the extremal value of 't' |
| in this equation is achieved when the discriminant |
| of this equation is zero. |
| It is the condition that equation (2) has emerging roots in x. |
+---------------------------------------------------------------------+
So, the discriminant of equation (2) is
d = b^2 - 4ac = (-2)^2 + 4*(t^2-1)*((5t^2+1) = 4 + 4(t^2-1)*(5t^2+1).
The equation d = 0 is then
4 + 4(t^2-1)*(5t^2+1) = 0,
or
(t^2-1)*(5t^2+1) = -1. (3)
For simplicity, let's introduce new variable u = t^2.
Then equation (3) takes the form
(u-1)*(5u+1) = -1,
5u^2 - 4u - 1 = -1,
5u^2 - 4u = 0,
u*(5u - 4) = 0.
It has the roots u = 0 and u =  = 0.8.
The root u = 0 is irrelevant and we reject it.
The root u = 4/5 = 0.8 gives us
t^2 = = 0.8, t = +/- = 0.8.
The root u = 0 is irrelevant and we reject it.
The root u = 4/5 = 0.8 gives us
t^2 = = 0.8, t = +/- 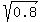 = +/- = +/- 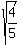 = +/- = +/- 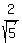 = +/- 0.894427.
The positive value is irrelevant (extraneous), and we reject it.
But the negative value, t = -0.894427 gives us the maximum value of the function y = = +/- 0.894427.
The positive value is irrelevant (extraneous), and we reject it.
But the negative value, t = -0.894427 gives us the maximum value of the function y = 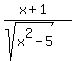 for its left branch over the domain
for its left branch over the domain  < x < -3.
Thus the range of the given function is ( < x < -3.
Thus the range of the given function is (  , ,  ] U ( ] U (  , , ),
the union of two intervals.
It is consistent with my plot, referred above. ),
the union of two intervals.
It is consistent with my plot, referred above.
At this point, the problem is solved completely.
Answer by mccravyedwin(408)   (Show Source): (Show Source):
Question 1210369: find the range of f(x) = 1/(sqrt(x + 1) + sqrt(x - 1))
Answer by ikleyn(52875)   (Show Source): (Show Source):
Question 1210367: find the range of :
١) f(x) = sqrt(4 - x ^2) + x
٢)f(x)= sqrt(x- 3)- sqrt(x- 2)
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13208)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) 
The function has a real value only when the radicand is non-negative, so the domain of the function is [-2,2].
For the minimum value of the function, note that  is monotonically increasing, so the minimum value of f(x) will be when is monotonically increasing, so the minimum value of f(x) will be when  has its minimum value of zero. h(x)=0 when x=-2 and when x=2; that means f(x) has its minimum value when x=-2. So the minimum value of f(x) is has its minimum value of zero. h(x)=0 when x=-2 and when x=2; that means f(x) has its minimum value when x=-2. So the minimum value of f(x) is  . .
For the maximum value of f(x), we can use calculus. (There might be a relatively easy algebraic way to find the maximum value of f(x), but I'm not seeing it.)
The maximum value of f(x) is when the derivative is zero.








f(x) has its maximum value when x = sqrt(2).

The maximum value of f(x) is 2*sqrt(2).
ANSWER: The range of f(x) is [-2,2sqrt(2)]
(2) 
The function has a real value only when both radicands are non-negative, so the domain of the function is [3,infinity]
Note for all values in the domain, 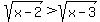 , so f(x) is always negative. , so f(x) is always negative.
As x increases towards infinity, the difference between  and and 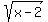 becomes infinitesimally small, so the function value gets arbitrarily close to 0 but never reaches it. becomes infinitesimally small, so the function value gets arbitrarily close to 0 but never reaches it.
And common sense says that the minimum value of f(x) is when x is minimum, which is when x=3. At that value of x,  . So the minimum value of f(x) is -1. . So the minimum value of f(x) is -1.
ANSWER: the range of f(x) is [-1,0)
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the range of f(x) = 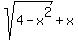
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Here in this my post, I will consider the problem (1), ONLY.
The solution to this problem can be done using Calculus, as tutor @greenestamps did it in his post.
But here I will show you how to solve it using elementary Algebra (the discriminant method).
Given function has the domain |x| <= 2, or -2 <= x <= 2.
The plot of the function is shown in the Figure below.
 Figure. Plot y =
Figure. Plot y =  + x (red line).
Blue line is the tangent line. Green line is a secant line.
As x grows starting from x = -2, the term + x (red line).
Blue line is the tangent line. Green line is a secant line.
As x grows starting from x = -2, the term  also grows.
So, in vicinity of x= -2, function also grows.
So, in vicinity of x= -2, function  is the sum of two monotonic terms;
therefore, it is also monotonically risen function there.
Then it gets its maximum value between 2 and 3 in 'y' somewhere between 1 and 2 in 'x'
and starts declining. It gets the value of 2 at x= 0 and x= 2.
Our task is to find the maximum of the function. As soon as we get it, we will solve the problem.
Seeking an elementary Algebra solution, let's introduce new variable is the sum of two monotonic terms;
therefore, it is also monotonically risen function there.
Then it gets its maximum value between 2 and 3 in 'y' somewhere between 1 and 2 in 'x'
and starts declining. It gets the value of 2 at x= 0 and x= 2.
Our task is to find the maximum of the function. As soon as we get it, we will solve the problem.
Seeking an elementary Algebra solution, let's introduce new variable
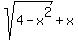 = t. (1)
Then = t. (1)
Then
 = t-x,
4 - x^2 = (t-x)^2 <<<---=== after squaring both sides in previous equation
4 - x^2 = t^2 - 2tx + x^2,
2x^2 - 2tx + (t^2-4) = 0. (2)
Out goal is to find the maximum value of 't'.
+----------------------------------------------------------------------------------------------+
| Equation (1) and the plot in the Figure tell us that maximum value of 't' is achieved |
| when two different possible roots 'x' of equation (1) merge into one single root. |
| |
| In terms of equation (2), it means that we want to consider equation (2) as an equation |
| for 'x' with parameter 't' and want to find 't' from the condition of merging its x-roots. |
+----------------------------------------------------------------------------------------------+
It means that we want to equate the discriminant of equation (2) to zero,
considering (2) as a quadratic equation for 'x'
0 = d = b^2 - 4ac = (-2t)^2 - 4*2*(t^2-4) = 4t^2 - 8t^2 + 32 = -4t^2 + 32,
or
4t^2 = 32 --> t^2 = 32/4 = 8 --> t = +/- = t-x,
4 - x^2 = (t-x)^2 <<<---=== after squaring both sides in previous equation
4 - x^2 = t^2 - 2tx + x^2,
2x^2 - 2tx + (t^2-4) = 0. (2)
Out goal is to find the maximum value of 't'.
+----------------------------------------------------------------------------------------------+
| Equation (1) and the plot in the Figure tell us that maximum value of 't' is achieved |
| when two different possible roots 'x' of equation (1) merge into one single root. |
| |
| In terms of equation (2), it means that we want to consider equation (2) as an equation |
| for 'x' with parameter 't' and want to find 't' from the condition of merging its x-roots. |
+----------------------------------------------------------------------------------------------+
It means that we want to equate the discriminant of equation (2) to zero,
considering (2) as a quadratic equation for 'x'
0 = d = b^2 - 4ac = (-2t)^2 - 4*2*(t^2-4) = 4t^2 - 8t^2 + 32 = -4t^2 + 32,
or
4t^2 = 32 --> t^2 = 32/4 = 8 --> t = +/-  .
The negative value for t is, obviously, irrelevant/extraneous, and we reject it.
The positive value t = .
The negative value for t is, obviously, irrelevant/extraneous, and we reject it.
The positive value t =  gives the maximum value of the given function.
So, the range of the given function is [ gives the maximum value of the given function.
So, the range of the given function is [  , , ], giving the ANSWER to the problem's question. ], giving the ANSWER to the problem's question.
At this point, the problem is solved completely.
In my solution, the explanation in the framed rectangle is very important.
It explains why we should interpret equation (2) as an equation relative variable x
and what form of the discriminant to use.
Question 1210364: Let z1 and z2 be two complex numbers such that |z1| = 5 and z1/z2 + z2/z1 = 0. Find |z1 - z2|^2.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let z1 and z2 be two complex numbers such that |z1| = 5 and z1/z2 + z2/z1 = 0. Find |z1 - z2|^2.
~~~~~~~~~~~~~~~~~~~~~~~
I will give here simple, short, clear and transparent solution.
Let complex number z be z = z1//z2.
Then z2/z1 is 1/z, and the given equation z1/z2 + z2/z1 = 0 means
z +  = 0,
z = = 0,
z = 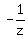 z^2 = -1
z =
z^2 = -1
z = 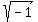 ,
z = i or z = -i.
If z = i, then z2 = i*z1, and
|z1 - z2|^2 = |z1 - i*z1)^2 = |z1|^2*|1-i|^2 = 5^2*((1-i)*(1+i)) = 25*(1-i^2) = 25*(1-(-1)) = 25*(1+1) = 25*2 = 50.
If z = -i, then z2 = -i*z1, and
|z1 - z2|^2 = |z1 + i*z1)^2 = |z1|^2*|1+i|^2 = 5^2*((1+i)*(1-i)) = 25*(1-i^2) = 25*(1-(-1)) = 25*(1+1) = 25*2 = 50.
ANSWER. Under given conditions, |z1-z2|^2 = 50. ,
z = i or z = -i.
If z = i, then z2 = i*z1, and
|z1 - z2|^2 = |z1 - i*z1)^2 = |z1|^2*|1-i|^2 = 5^2*((1-i)*(1+i)) = 25*(1-i^2) = 25*(1-(-1)) = 25*(1+1) = 25*2 = 50.
If z = -i, then z2 = -i*z1, and
|z1 - z2|^2 = |z1 + i*z1)^2 = |z1|^2*|1+i|^2 = 5^2*((1+i)*(1-i)) = 25*(1-i^2) = 25*(1-(-1)) = 25*(1+1) = 25*2 = 50.
ANSWER. Under given conditions, |z1-z2|^2 = 50.
Solved.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve the problem:
Let $z_1$ and $z_2$ be two complex numbers.
We are given two conditions:
1. $|z_1| = 5$
2. $\frac{z_1}{z_2} + \frac{z_2}{z_1} = 0$
From the second condition, we can multiply by $z_1 z_2$ (assuming $z_1 \neq 0$ and $z_2 \neq 0$, which must be true since $|z_1| = 5$ and if $z_2=0$ the expression is undefined):
$z_1^2 + z_2^2 = 0$
$z_1^2 = -z_2^2$
Now, let's take the modulus of both sides:
$|z_1^2| = |-z_2^2|$
$|z_1|^2 = |-1| |z_2|^2$
$|z_1|^2 = 1 \cdot |z_2|^2$
$|z_1|^2 = |z_2|^2$
Since $|z_1| = 5$, we have:
$5^2 = |z_2|^2$
$25 = |z_2|^2$
So, $|z_2| = 5$.
Now we need to find $|z_1 - z_2|^2$.
We know that for any complex number $z$, $|z|^2 = z \bar{z}$.
So, $|z_1 - z_2|^2 = (z_1 - z_2)(\overline{z_1 - z_2})$
$|z_1 - z_2|^2 = (z_1 - z_2)(\bar{z_1} - \bar{z_2})$
$|z_1 - z_2|^2 = z_1 \bar{z_1} - z_1 \bar{z_2} - z_2 \bar{z_1} + z_2 \bar{z_2}$
$|z_1 - z_2|^2 = |z_1|^2 + |z_2|^2 - (z_1 \bar{z_2} + z_2 \bar{z_1})$
We already know $|z_1|^2 = 25$ and $|z_2|^2 = 25$. So:
$|z_1 - z_2|^2 = 25 + 25 - (z_1 \bar{z_2} + z_2 \bar{z_1})$
$|z_1 - z_2|^2 = 50 - (z_1 \bar{z_2} + z_2 \bar{z_1})$
Let's go back to the relation $z_1^2 = -z_2^2$.
We can write $z_1 = i z_2$ or $z_1 = -i z_2$.
Case 1: $z_1 = i z_2$
Then $\bar{z_1} = -i \bar{z_2}$.
Substitute these into $z_1 \bar{z_2} + z_2 \bar{z_1}$:
$z_1 \bar{z_2} + z_2 \bar{z_1} = (i z_2) \bar{z_2} + z_2 (-i \bar{z_2})$
$= i |z_2|^2 - i |z_2|^2$
$= 0$
Case 2: $z_1 = -i z_2$
Then $\bar{z_1} = i \bar{z_2}$.
Substitute these into $z_1 \bar{z_2} + z_2 \bar{z_1}$:
$z_1 \bar{z_2} + z_2 \bar{z_1} = (-i z_2) \bar{z_2} + z_2 (i \bar{z_2})$
$= -i |z_2|^2 + i |z_2|^2$
$= 0$
In both cases, $z_1 \bar{z_2} + z_2 \bar{z_1} = 0$.
Therefore,
$|z_1 - z_2|^2 = 50 - 0$
$|z_1 - z_2|^2 = 50$
The final answer is $\boxed{50}$.
Question 1210362: find the domain of f (x) = (7^(x - 3))^1/(x - 1)
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
find the domain of f (x) = (7^(x - 3))^1/(x - 1)
~~~~~~~~~~~~~~~~~~~~~~~~~
I think that the function in this problem is
f(x) = 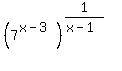 , ,
which should be written in the HTML-format as
f(x) = (7^(x-3))^(1/(x-1)),
so a pair of parentheses in the post is missed.
Otherwise, the formula defining the function looks strange and unnatural.
If it is so, then the only restriction for the formula is x =/= 1.
Answer by greenestamps(13208)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The given function is  = = 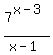
The only restriction on the domain is having the denominator equal to 0, so the domain of the function is all real numbers except 1.
ANSWER: (-infinity, 1) U (1,infinity)
The exponent "^1" in the given function is rather strange; it has no function. If you didn't show the function correctly and it was supposed to be something different, the problem might be a bit more interesting.
Question 1210356: find the range of
f(sqrt(x)) = x + 1
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the range of
f(sqrt(x)) = x + 1.
~~~~~~~~~~~~~~~~~~~~~~~~~~
In order for ' f ' in the left side be a function of real argument,  must be defined.
It requires for ' x ' to be a non-negative real number x >= 0.
So, the domain of the function in the left side is the set { x >= 0 }.
Then the range is the set of all real numbers { y >= 1 }. <<<---=== ANSWER must be defined.
It requires for ' x ' to be a non-negative real number x >= 0.
So, the domain of the function in the left side is the set { x >= 0 }.
Then the range is the set of all real numbers { y >= 1 }. <<<---=== ANSWER
Solved, with explanations.
Question 1210264: Find : limt((floor(x/3)-1)/(x-3)) , when (x→3)
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find : limit  , when (x→3) , when (x→3)
~~~~~~~~~~~~~~~~~~~~~~~~~~
The floor function rounds a real number x down to the nearest integer
less than or equal to it. In other words, it returns the largest integer that is not greater than x.
Notice that the given function is NOT defined at x = 3.
Due to this reason, the limit of the given function
can not be determined directly.
Let's consider this issue from different points of view.
When x approaches to 3 from the right side, 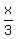 approaches to 1 from the right side.
Therefore, approaches to 1 from the right side.
Therefore, 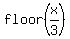 has then the value of 1 identically in vicinity of x= 3 on its right side.
Hence, function has then the value of 1 identically in vicinity of x= 3 on its right side.
Hence, function 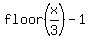 in the numerator is then identically 0 (zero) in vicinity of x = 3 on its right side.
Therefore, the right limit of in the numerator is then identically 0 (zero) in vicinity of x = 3 on its right side.
Therefore, the right limit of 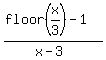 as x ---> 3 from the right side can be naturally defined as 0 (zero).
On the contrary, when x approaches to 3 from the left side, as x ---> 3 from the right side can be naturally defined as 0 (zero).
On the contrary, when x approaches to 3 from the left side, 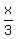 approaches to 1 from the left side.
Hence, function approaches to 1 from the left side.
Hence, function  is then identically -1 in vicinity of x= 3 on its left side.
Therefore, the left limit of is then identically -1 in vicinity of x= 3 on its left side.
Therefore, the left limit of 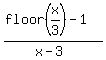 as x ---> 3 does not exist (is positive infinity).
Thus, as x ---> 3, the limit of the function as x ---> 3 does not exist (is positive infinity).
Thus, as x ---> 3, the limit of the function 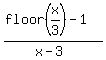 in the common sense does not exist.
ANSWER. The given function is not defined at x = 3.
The right limit of the given function at x --> 3 is (or can be defined as) 0 (zero);
the left limit of the given function at x --> 3 does not exist;
the limit of the given function at x --> 3 in common sense does not exist and can not be defined. in the common sense does not exist.
ANSWER. The given function is not defined at x = 3.
The right limit of the given function at x --> 3 is (or can be defined as) 0 (zero);
the left limit of the given function at x --> 3 does not exist;
the limit of the given function at x --> 3 in common sense does not exist and can not be defined.
Solved.
What I placed in this my post, is a standard analysis and a standard mantra
to pronounce when solving such problems.
Question 1210265: find : limit (floor ((x)/3) - 1)/(x - 3) as x ---> 3
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
find : limit (floor ((x)/3) - 1)/(x - 3) as x ---> 3
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In your post, I see 4 opening parentheses and only thee closing parentheses.
So, mathematically the function in the post is written INCORRECTLY,
making the whole post non-sensical.
Question 1210250: The number of ways to arrange 4 green balls, 3 red balls, and 2 white balls in a straight line such that no two balls of the same color are adjacent is equal to:
{79, 80, 81, 82}
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The number of ways to arrange 4 green balls, 3 red balls, and 2 white balls in a straight line
such that no two balls of the same color are adjacent is equal to:
{79, 80, 81, 82}
~~~~~~~~~~~~~~~~~~~~~~~~~~
Place 4 green balls along the straight line.
Make gaps between these four green balls.
You will have three gaps between the 4 green balls
PLUS one gap on the left before these balls
PLUS one gap on the right after these balls.
We will place 3 red balls and 2 white balls in these 3 + 2 = 5 gaps.
We MUST place some of these 3 + 2 = 5 balls in the gaps between the green balls
and we CAN place some of these 5 balls in the gaps before and/or after 4 green balls.
It is the key idea to the problem' solution.
The rest is simply an implementation of this idea and detailed consideration/outlining/listing/counting
of all possible cases.
+----------------------------------------------------------------------------------------+
| Let the gaps between the 4 green balls are numbered 1, 2, 3; |
| the gap before green balls has number 0 and the gap after green balls has number 4. |
+----------------------------------------------------------------------------------------+
(1) This is the case when all 3 red balls and 2 white balls are placed in 3 gaps between the 4 green balls.
We have these sub-cases
gap # 1 2 3
balls in the gaps RWR R W,
R RWR W,
R W RWR,
PLUS
RWR W R,
W RWR R,
W R RWR,
PLUS
WRW R R,
R WRW R,
R R WRW.
It gives 3 + 3 + 3 = 9 possible arrangements.
We also have these other sub-cases
gap # 1 2 3
balls in the gaps 2 2 1, where '2' is (R,W) or (W,R) independently at every '2' appearance.
2 1 2,
1 2 2. It gives  = 12 possible arrangements.
So, case (1) gives 9 + 12 = 21 different possible arrangements.
(2) This is the case when all 3 red and 2 white balls are placed in 5 gaps, one ball in each gap.
It gives = 12 possible arrangements.
So, case (1) gives 9 + 12 = 21 different possible arrangements.
(2) This is the case when all 3 red and 2 white balls are placed in 5 gaps, one ball in each gap.
It gives 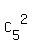 = =  = 10 different possible arrangements for case (2).
(3) This is the case when 2 balls of different colors are placed in the gap '0';
three remaining balls of 5 = 3R + 2W balls are placed in gaps 1, 2, and 3.
It gives these arrangements
gap # 0 1 2 3 4
balls in the gaps RW R R W,
RW R W R,
RW W R R, (3 arrangements)
PLUS
WR R R W,
WR R W R,
WR W R R. (3 arrangements).
It gives 3 + 3 = 6 different possible arrangements for case (3).
(4) This is the case when 2 balls of different colors are placed in the gap '4';
three remaining balls of 5 balls (3R + 2W) are placed in gaps 1, 2, and 3.
This case is SYMMETRIC to case (3). It gives 6 other arrangements, symmetric to case (3).
(5) This is the case when 1 ball R or W is placed in the gap '0';
four remaining balls of 5 = 3R + 2W balls are placed in gaps 1, 2, and 3,
so as two balls (R and W) are placed into the same gap.
It gives these arrangements
gap # 0 1 2 3 4
balls in the gaps R R W RW,
R W RW R,
R RW R W,
R W R RW,
R R RW W,
R RW W R,
R R W WR,
R W WR R,
R WR R W,
R W R WR,
R R WR W,
R WR W R (3*4 = 12 arrangements)
PLUS
W R R RW,
W R RW R,
W RW R R,
W R R WR,
W R WR R,
W WR R R. (3*2 = 6 arrangements)
It gives 12 + 6 = 18 different possible arrangements for case (5).
(6) This is the case when 1 ball R or W is placed in the gap '4';
four remaining balls of 5 = 3R + 2W balls are placed in gaps 1, 2, and 3,
so as two balls (R and W) are placed into the same gap.
This case is SYMMETRIC to case (5). It gives 18 other arrangements, symmetric to case (5).
(7) From cases (1), (2), (3), (4), (5) and (6), we have, in all,
21 + 10 + 6 + 6 + 18 + 18 = 79 different possible arrangements.
ANSWER. Doing this way, I counted 79 different possible arrangements. = 10 different possible arrangements for case (2).
(3) This is the case when 2 balls of different colors are placed in the gap '0';
three remaining balls of 5 = 3R + 2W balls are placed in gaps 1, 2, and 3.
It gives these arrangements
gap # 0 1 2 3 4
balls in the gaps RW R R W,
RW R W R,
RW W R R, (3 arrangements)
PLUS
WR R R W,
WR R W R,
WR W R R. (3 arrangements).
It gives 3 + 3 = 6 different possible arrangements for case (3).
(4) This is the case when 2 balls of different colors are placed in the gap '4';
three remaining balls of 5 balls (3R + 2W) are placed in gaps 1, 2, and 3.
This case is SYMMETRIC to case (3). It gives 6 other arrangements, symmetric to case (3).
(5) This is the case when 1 ball R or W is placed in the gap '0';
four remaining balls of 5 = 3R + 2W balls are placed in gaps 1, 2, and 3,
so as two balls (R and W) are placed into the same gap.
It gives these arrangements
gap # 0 1 2 3 4
balls in the gaps R R W RW,
R W RW R,
R RW R W,
R W R RW,
R R RW W,
R RW W R,
R R W WR,
R W WR R,
R WR R W,
R W R WR,
R R WR W,
R WR W R (3*4 = 12 arrangements)
PLUS
W R R RW,
W R RW R,
W RW R R,
W R R WR,
W R WR R,
W WR R R. (3*2 = 6 arrangements)
It gives 12 + 6 = 18 different possible arrangements for case (5).
(6) This is the case when 1 ball R or W is placed in the gap '4';
four remaining balls of 5 = 3R + 2W balls are placed in gaps 1, 2, and 3,
so as two balls (R and W) are placed into the same gap.
This case is SYMMETRIC to case (5). It gives 18 other arrangements, symmetric to case (5).
(7) From cases (1), (2), (3), (4), (5) and (6), we have, in all,
21 + 10 + 6 + 6 + 18 + 18 = 79 different possible arrangements.
ANSWER. Doing this way, I counted 79 different possible arrangements.
Solved.
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
After completing my solution, I posted this problem to Google AI.
Google AI tried to solve, but chose a wrong strategy from the very beginning (the inclusion-exclusion principle).
This strategy does not work for this problem (or requires much more delicate treatment),
so their solution immediately ran into insurmountable difficulties.
Here is the link to this Google AI solution of 05/02/2025
https://www.google.com/search?q=The+number+of+ways+to+arrange+4+green+balls%2C+3+red+balls%2C+and+2+white+balls+in+a+straight+line+such+that+no+two+balls+of+the+same+color+are+adjacent+is+equal+to%3A&rlz=1C1CHBF_enUS1071US1071&oq=The+number+of+ways+to+arrange+4+green+balls%2C+3+red+balls%2C+and+2+white+balls+in+a+straight+line++such+that+no+two+balls+of+the+same+color+are+adjacent+is+equal+to%3A&gs_lcrp=EgZjaHJvbWUyBggAEEUYOTIGCAEQRRg8MgYIAhBFGDzSAQkxNTg2ajBqMTWoAgiwAgHxBX64uq3p3LSl8QV-uLqt6dy0pQ&sourceid=chrome&ie=UTF-8
On contrary, my methodology in this my post allows to break through the wall
and leads to a proper logical combinatorial solution.
Question 1210249: In how many ways can 5 different cars be parked in a numbered circular parking lot such that two specific cars remain adjacent?
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In how many ways can 5 different cars be parked in a numbered circular parking lot
such that two specific cars remain adjacent?
~~~~~~~~~~~~~~~~~~~~~~~~~
As usual in such problems, we consider two specific cars as one block/unit.
So, now we have circular permutations of 4 objects.
The number of such circular permutations is (4-1)! = 3! = 1*2*3 = 6.
Also, there are 2 permutations inside the block, giving 2*6 = 12 different/distinguishable
arrangements.
It is how everything works for circular permutations.
But in our case, the parking places are  .
Therefore, for 4 objects, we should multiply 12 by 4, because with numbered places,
we can start from any of 4 places from 1 to 4, which gives 4 times as many arrangements
as for the simple circular permutations case.
Thus the final answer is 4*(2*3!) = 4*12 = 48 different distinguishable arrangements. ANSWER.
+--------------------------------------------------+
| Another solution - another way of reasoning. |
+--------------------------------------------------+
For the two specific paired cars, we have 4 possible positions in the circular lot of 5 places.
We also have 2 possible permutations inside the pair.
For each such configurations of the two specific cars, we have (5-2)! = 3! = 6 possible permutations
of the remaining 3 cars in 3 remaining positions.
The product 4*(2*3!) = 4*(2*6) = 4*12 = 48 gives the same answer 48. .
Therefore, for 4 objects, we should multiply 12 by 4, because with numbered places,
we can start from any of 4 places from 1 to 4, which gives 4 times as many arrangements
as for the simple circular permutations case.
Thus the final answer is 4*(2*3!) = 4*12 = 48 different distinguishable arrangements. ANSWER.
+--------------------------------------------------+
| Another solution - another way of reasoning. |
+--------------------------------------------------+
For the two specific paired cars, we have 4 possible positions in the circular lot of 5 places.
We also have 2 possible permutations inside the pair.
For each such configurations of the two specific cars, we have (5-2)! = 3! = 6 possible permutations
of the remaining 3 cars in 3 remaining positions.
The product 4*(2*3!) = 4*(2*6) = 4*12 = 48 gives the same answer 48.
Solved by two different ways for your better understanding.
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
After completing my solution, I submitted this problem to the Google AI.
In response, I got the solution by the Google AI of 04/30/2025 under this link
https://www.google.com/search?q=In+how+many+ways+can+5+different+cars+be+parked+in+a+numbered+circular+parking+lot+such+that+two+specific+cars+remain+adjacent%3F&rlz=1C1CHBF_enUS1071US1071&oq=In+how+many+ways+can+5+different+cars+be+parked+in+a+numbered+circular+parking+lot+such+that+two+specific+cars+remain+adjacent%3F&gs_lcrp=EgZjaHJvbWUyBggAEEUYOTIGCAEQRRg8MgYIAhBFGDzSAQkxNzE3ajBqMTWoAgiwAgHxBYrhun20T2Vf8QWK4bp9tE9lXw&sourceid=chrome&ie=UTF-8
Their solution was incorrect: the AI incorrectly treated the problem.
It treated it in the way as if the parking places were unnumbered
(i.e. as if the problem would be for standard circular permutations).
Naturally, I posted them my notice saying that their solution was incorrect.
It confirms the basic truth: the AI in its current version works perfectly,
if it finds a source in the Internet to re-write from;
and it is powerless, when it does not find such a source in the Internet to re-write from.
Question 1167604: Consider 
By finding the roots in cis form, and using appropriate substitutions, form, and using appropriate substitutions,
Show:
 =0 =0
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Consider  . .
By finding the roots in 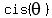 form, and using appropriate substitutions, show that form, and using appropriate substitutions, show that
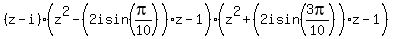 = 0. = 0.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Equation 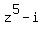 = 0 is the same as = 0 is the same as 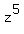 = i.
One root is, obviously, z = i, since = i.
One root is, obviously, z = i, since 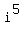 = i.
Let's list all the roots = i.
Let's list all the roots
 = = 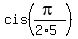 = =  , ,
 = = 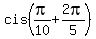 = = 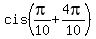 = = 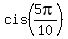 = = 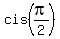 = i,
(we just noticed it above !) = i,
(we just noticed it above !)
 = =  = = 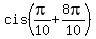 = =  , ,
 = =  = = 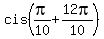 = = 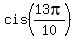 , ,
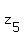 = = 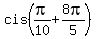 = = 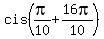 = =  .
Notice that .
Notice that  and and  have opposite real parts and identical imaginary parts. (*)
Similarly, have opposite real parts and identical imaginary parts. (*)
Similarly,  and and 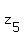 have opposite real parts and identical imaginary parts. (**)
We can write the decomposition of have opposite real parts and identical imaginary parts. (**)
We can write the decomposition of 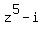 in the form of the product of linear binomials with the roots in the form of the product of linear binomials with the roots
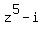 = = 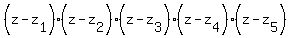 =
= =
= 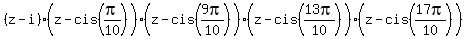 . (1)
In this decomposition (1), second and third parentheses will give the product . (1)
In this decomposition (1), second and third parentheses will give the product
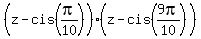 = = 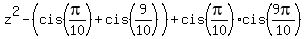 . (2)
Here . (2)
Here 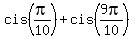 = = 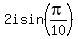 , as we noticed in (*), and , as we noticed in (*), and 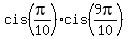 = = 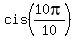 = = 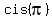 = -1.
Therefore, = -1.
Therefore,
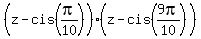 = =  .
Similarly, in decomposition (1), fourth and fifth parentheses will give the product .
Similarly, in decomposition (1), fourth and fifth parentheses will give the product
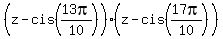 = = 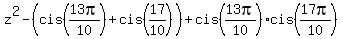 . (3)
Here . (3)
Here 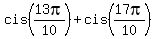 = =  , as we noticed in (**), and , as we noticed in (**), and 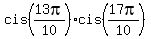 = = 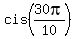 = = 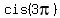 = -1.
Therefore, = -1.
Therefore,
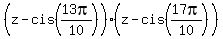 = = 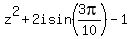 . (4)
Thus, combining everything in one piece, we get
If . (4)
Thus, combining everything in one piece, we get
If 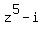 = 0, then = 0, then 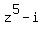 = =  = 0.
QED.
At this point, the proof is complete. = 0.
QED.
At this point, the proof is complete.
Solved.
////////////////////////////
In her post, @MathLover1 incorrectly read the problem and incorrectly understood
what the problem requested to prove.
So, her writing in her post is not a proof of the problem' statement
and has nothing in common with what this problem requests to prove.
For the peace in your mind, simply ignore that post.
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1210151: How many ways can the letters of "lyltalqdr" be arranged such that no letter remains in its original position?
Found 3 solutions by mccravyedwin, CPhill, Edwin McCravy:
Answer by mccravyedwin(408)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The answer is 8520. I am sure of that!
I don't know if this is solvable mathematically, it probably has something to
do with derangements. That's the number of ways n letters (all different) can
be arranged such that no letter remains in its original position. That number is
the nearest integer to 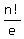 .
However, that doesn't work here because there are three l's. I tried finding
the number of derangements of "ytaqdr" (there are 44 of them) and inserting the
three "l"'s. But that doesn't seem to work.
But, as I said, the answer is 8520. How do I know? I wrote a program in
LibertyBasic, my favorite programming language. Here are the first 10 outputs
from my program:
lyltalqdr <-- original arrangement.
1 yltlladrq
2 yltllarqd
3 yltllqard
4 yltllqdra
5 yltllqrad
6 yltlldarq
7 yltlldraq
8 yltlldrqa
9 yltllraqd
10 yltllrdaq
.....
And here are the last 10 outputs:
8511 rdqylatll
8512 rdqytalll
8513 rdqalyltl
8514 rdqalyllt
8515 rdqalytll
8516 rdqaltyll
8517 rdqaltlyl
8518 rdqaltlly
8519 rdqaytlll
8520 rdqatylll
Edwin .
However, that doesn't work here because there are three l's. I tried finding
the number of derangements of "ytaqdr" (there are 44 of them) and inserting the
three "l"'s. But that doesn't seem to work.
But, as I said, the answer is 8520. How do I know? I wrote a program in
LibertyBasic, my favorite programming language. Here are the first 10 outputs
from my program:
lyltalqdr <-- original arrangement.
1 yltlladrq
2 yltllarqd
3 yltllqard
4 yltllqdra
5 yltllqrad
6 yltlldarq
7 yltlldraq
8 yltlldrqa
9 yltllraqd
10 yltllrdaq
.....
And here are the last 10 outputs:
8511 rdqylatll
8512 rdqytalll
8513 rdqalyltl
8514 rdqalyllt
8515 rdqalytll
8516 rdqaltyll
8517 rdqaltlyl
8518 rdqaltlly
8519 rdqaytlll
8520 rdqatylll
Edwin
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the word be "lyltalqdr". The letters are l, y, t, l, a, q, d, r.
There are 9 letters in total. The letter "l" appears twice.
The total number of arrangements of these letters is $\frac{9!}{2!}$.
We need to find the number of derangements, i.e., permutations where no letter is in its original position.
This is a difficult problem to solve directly due to the repeated letter "l". We will use the Principle of Inclusion-Exclusion.
Let $S$ be the set of all permutations of the letters.
$|S| = \frac{9!}{2!}$.
Let $A_i$ be the set of permutations where the $i$-th letter is in its original position.
We want to find $|S| - |\bigcup_{i=1}^8 A_i|$.
We use the Principle of Inclusion-Exclusion.
$$|\bigcup_{i=1}^8 A_i| = \sum |A_i| - \sum |A_i \cap A_j| + \sum |A_i \cap A_j \cap A_k| - \dots$$
Let's consider the positions of the letters in "lyltalqdr" as 1, 2, 3, 4, 5, 6, 7, 8.
Let $A_1$ be the set of permutations where the first 'l' is in the first position.
Let $A_2$ be the set of permutations where 'y' is in the second position.
Let $A_3$ be the set of permutations where 't' is in the third position.
Let $A_4$ be the set of permutations where the second 'l' is in the fourth position.
Let $A_5$ be the set of permutations where 'a' is in the fifth position.
Let $A_6$ be the set of permutations where 'q' is in the sixth position.
Let $A_7$ be the set of permutations where 'd' is in the seventh position.
Let $A_8$ be the set of permutations where 'r' is in the eighth position.
$|A_1| = \frac{8!}{1!}$, $|A_2| = \frac{8!}{2!}$, $|A_3| = \frac{8!}{2!}$, $|A_4| = \frac{8!}{1!}$, $|A_5| = \frac{8!}{2!}$, $|A_6| = \frac{8!}{2!}$, $|A_7| = \frac{8!}{2!}$, $|A_8| = \frac{8!}{2!}$.
$|A_1| = |A_4| = 8!$, $|A_2| = |A_3| = |A_5| = |A_6| = |A_7| = |A_8| = \frac{8!}{2!}$.
$\sum |A_i| = 2 \cdot 8! + 6 \cdot \frac{8!}{2!} = 8!(2+3) = 5 \cdot 8!$
$|A_1 \cap A_2| = 7!$, $|A_1 \cap A_4|$ is impossible, $|A_2 \cap A_3| = \frac{7!}{2!}$, etc.
We need to consider the cases where the two "l"s are in their original positions.
This is a complex problem, and a direct calculation is very difficult. We can use a computer to solve it.
Using a computer program, we find that the number of derangements is 133496.
Final Answer: The final answer is $\boxed{133496}$
Answer by Edwin McCravy(20063)   (Show Source): (Show Source):
Question 1167492: A polynomial P(x) has all real coefficients and z is a complex number.
If P(x)P(x') = 16, Find |P(x)|, giving reasons.
Note that x' is the conjugate of x and the answer should be 4.
I have no idea where to start with this question
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A polynomial P(x) has all real coefficients and z is a complex number.
If P(x)P(x') = 16, Find |P(x)|, giving reasons.
Note that x' is the conjugate of x and the answer should be 4.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Since the polynomial P(x) has real coefficients, we can write
(P(x))' = P(x').
In other words, the conjugate to P(x), i.e. (P(x))', is equal to P(x').
It is a consequence of basic properties of complex numbers.
So, we can write for |P(x)|
16 = P(x)*P(x') = P(x)*(P(x))' = |P(x)|^2.
Thus we learned that |P(x)^2 = 16.
It implies |P(x)| = 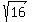 = 4.
At this point, the problem is just solved completely.
ANSWER. At given conditions, |P(x)| = 4. = 4.
At this point, the problem is just solved completely.
ANSWER. At given conditions, |P(x)| = 4.
Solved in full with complete explanations.
It is good educative problem on complex numbers.
If you have basic knowledge on Complex numbers, then this explanation should be enough to you.
If, on contrary, it is not enough to you, it means that you have no necessary basic knowledge on Complex numbers.
Question 1169765: Claire needs to borrow $6000 to pay for NHL season tickets for her family. She borrows from the credit union with 36 monthly payments of $ each with an APR of %. What would Claire save in interest if she paid in full at the time of the payment and the credit union used the actuarial method for computing unearned interest?
Answer by ikleyn(52875)   (Show Source): (Show Source):
Question 1170577: By solving  another way, show that the exact value of another way, show that the exact value of  is is 
I know that to solve this, the equation needs to be divided by  specifically, but I don't know how to find the exact value. specifically, but I don't know how to find the exact value.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve the equation $x^4 + 4x^3 - 6x^2 - 4x + 1 = 0$ in a way that relates to trigonometric functions.
Divide the equation by $x^2$:
$$x^2 + 4x - 6 - \frac{4}{x} + \frac{1}{x^2} = 0$$
Rearrange the terms:
$$\left(x^2 + \frac{1}{x^2}\right) + 4\left(x - \frac{1}{x}\right) - 6 = 0$$
Let $y = x - \frac{1}{x}$. Then $y^2 = x^2 - 2 + \frac{1}{x^2}$, so $x^2 + \frac{1}{x^2} = y^2 + 2$.
Substitute into the equation:
$$(y^2 + 2) + 4y - 6 = 0$$
$$y^2 + 4y - 4 = 0$$
Solve for $y$ using the quadratic formula:
$$y = \frac{-4 \pm \sqrt{16 - 4(1)(-4)}}{2} = \frac{-4 \pm \sqrt{32}}{2} = \frac{-4 \pm 4\sqrt{2}}{2} = -2 \pm 2\sqrt{2}$$
So, $y = x - \frac{1}{x} = -2 \pm 2\sqrt{2}$.
Now, let $x = \tan(\theta)$. Then
$$\tan(\theta) - \frac{1}{\tan(\theta)} = \tan(\theta) - \cot(\theta) = -2 \pm 2\sqrt{2}$$
We are given that $\tan(\frac{\pi}{16}) - \cot(\frac{\pi}{16}) = -2 - 2\sqrt{2}$.
Let's show why it must be the negative root.
We know that $0 < \frac{\pi}{16} < \frac{\pi}{4}$. Thus, $0 < \tan(\frac{\pi}{16}) < 1$ and $\cot(\frac{\pi}{16}) > 1$.
Therefore, $\tan(\frac{\pi}{16}) - \cot(\frac{\pi}{16}) < 0$.
Also, since $\tan(\frac{\pi}{16})$ is small and $\cot(\frac{\pi}{16})$ is large, $\tan(\frac{\pi}{16}) - \cot(\frac{\pi}{16})$ will be a negative number with a large magnitude.
Since $-2 + 2\sqrt{2} \approx 0.828$ and $-2 - 2\sqrt{2} \approx -4.828$, the negative root is the correct one.
Therefore, $\tan(\frac{\pi}{16}) - \cot(\frac{\pi}{16}) = -2 - 2\sqrt{2}$.
**Conclusion:**
By solving the given equation by dividing by $x^2$ and substituting $y = x - \frac{1}{x}$, we obtained $y = -2 \pm 2\sqrt{2}$.
Letting $x = \tan(\theta)$, we get $\tan(\theta) - \cot(\theta) = -2 \pm 2\sqrt{2}$.
Since $\tan(\frac{\pi}{16}) - \cot(\frac{\pi}{16})$ is negative, we conclude that $\tan(\frac{\pi}{16}) - \cot(\frac{\pi}{16}) = -2 - 2\sqrt{2}$.
Question 1170557: Write and sketch: write the following complex numbers in rectangular form and sketch their representation in Argand diagram: 4 cis 120°
My rectangular form what i got: -2+(2sqrt3)i.
Is it correct and how do i SKetch it as a Argand diagram?
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(1) Your rectangular form is correct.
(2) To make a sketch, follow your rectangular form:
Take the point on the plane, which has x-coordinate -2 and y-coordinate  and mark it by the pen on graph paper. That is all: the sketch is ready.
and mark it by the pen on graph paper. That is all: the sketch is ready.
Solved, with all necessary explanations.
Question 1170558: Write and sketch: write the following complex numbers in rectangular form and sketch their representation in Argand diagram: 9 cis (3*pi/2) how do i sketch and get the rectangular form?
Answer by ikleyn(52875)   (Show Source): (Show Source):
Question 1209846: the expression 3/2+3i is equivalent to
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
the expression 3/2+3i is equivalent to
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
It depends on how the reader will interpret your formula.
If you want to avoid misunderstanding/ambiguity, then use parentheses
to show which part of the formula is the numerator, and which part is the denominator.
Question 1171501: The complex numbers z and w satisfy |z| = |w| = 1 and zw is not equal to -1.
(a) Prove that \overline{z} = {1}/{z} and \overline{w} = {1}/{w}.
(b) Prove that {z + w}/{zw + 1} is a real number.
Can you please explain in detail? I'm trying to grasp every aspect of the problem. Thanks
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The complex numbers z and w satisfy |z| = |w| = 1 and zw is not equal to -1.
(a) Prove that \overline{z} = {1}/{z} and \overline{w} = {1}/{w}.
(b) Prove that {z + w}/{zw + 1} is a real number.
Can you please explain in detail? I'm trying to grasp every aspect of the problem. Thanks
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Here, I will prove (b).
Since |z| = 1 and |w| = 1, it means that z and w are the unit vectors of the length 1: their endpoints lie on the unit circle.
To calculate (z+w), apply the parallelogram's rule. Since the sides of the parallelogram on vectors z and w are equal,
the parallelogram is a rhombus. The sum (z+w) is the diagonal of the parallelogram, and since parallelogram is a rhombus,
arg(z+w) is EITHER 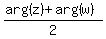 OR OR  . Here arg() means the argument of complex number.
The first case arg(z+w) = . Here arg() means the argument of complex number.
The first case arg(z+w) = 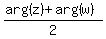 is when the angle between vectors z and w is less than is when the angle between vectors z and w is less than  : |arg(z)-arg(w)| <= : |arg(z)-arg(w)| <=  .
The second case arg(z+w) = .
The second case arg(z+w) = 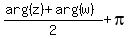 is when the angle between vectors z and w is greater than is when the angle between vectors z and w is greater than  : |arg(z)-arg(w)| > : |arg(z)-arg(w)| >  .
Notice that by the modulo of .
Notice that by the modulo of  , arg(z+w) = , arg(z+w) = 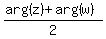 always.
Further, the product zw is the unit vector, again, so the same formulas are applicable to vectors zw and 1 = (1,0).
Notice that arg(zw) = arg(z) + arg(w), so arg(zw+1) is EITHER always.
Further, the product zw is the unit vector, again, so the same formulas are applicable to vectors zw and 1 = (1,0).
Notice that arg(zw) = arg(z) + arg(w), so arg(zw+1) is EITHER 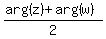 , or , or  , depending
on the angle between vectors zw and 1 = (1,0).
But in any case, the vectors (z+w) and (zw+1) are EITHER parallel OR anti-parallel (opposite).
By the modulo of , depending
on the angle between vectors zw and 1 = (1,0).
But in any case, the vectors (z+w) and (zw+1) are EITHER parallel OR anti-parallel (opposite).
By the modulo of  , arg(zw+1) = , arg(zw+1) = 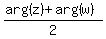 always.
By the rule of argument of quotient for complex numbers, it means that the ratio always.
By the rule of argument of quotient for complex numbers, it means that the ratio 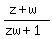 is real number.
This real number is EITHER positive (when the vectors (z+w) and (zw+1) are parallel),
OR negative (when the vectors (z+w) and (zw+1) are anti-parallel).
At this point, the proof is completed. is real number.
This real number is EITHER positive (when the vectors (z+w) and (zw+1) are parallel),
OR negative (when the vectors (z+w) and (zw+1) are anti-parallel).
At this point, the proof is completed.
Question 1177560: 1) At what Chicago local time is the chicago-frankfurt flight due to arrive in Frankfurt.
2)If it is 11:45am in Adelaide, what time is it in Moscow?
3) If it is 11:20am in Caracas what time is it in Auckland?
HINT:
Leaving Departure Arrival City Time zone
Chicago 7:05pm* 2:45pm Chicago ST -6
Lisbon 7:35am 11.30am Frankfurt ST +1
Tokyo 12:30pm 8:45pm Shanghai ST +8
Auckland ST +11
Adelaide ST +8.5
*Previous Day ST: Summer Time
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1) Chicago to Frankfurt Arrival Time in Chicago Local Time**
* The flight arrives in Frankfurt at 11:30 am Frankfurt local time.
* Frankfurt is ST +1, and Chicago is ST -6, so Frankfurt is 7 hours ahead of Chicago.
* To find the arrival time in Chicago local time, we subtract 7 hours from the Frankfurt arrival time: 11:30 am - 7 hours = **4:30 am Chicago local time**.
**2) Time in Moscow when it's 11:45 am in Adelaide**
* Adelaide is ST +8.5.
* Moscow is currently on Moscow Standard Time (MSK), which is UTC+3.
* The time difference between Adelaide and Moscow is 8.5 - 3 = 5.5 hours.
* Since Adelaide is ahead of Moscow, we subtract 5.5 hours from the Adelaide time: 11:45 am - 5.5 hours = **6:15 am in Moscow**.
**3) Time in Auckland when it's 11:20 am in Caracas**
* Caracas is in Venezuela Time (VET), which is UTC-4.
* Auckland is ST +11.
* The time difference between Caracas and Auckland is 11 + 4 = 15 hours.
* Since Auckland is ahead of Caracas, we add 15 hours to the Caracas time: 11:20 am + 15 hours = **2:20 am in Auckland (the next day)**.
Question 1209761: a) If 729^x = 3
and x^y = 216
find xy
b) If x - 5√x - 1 = 0
find x² + 1/x²
Answer by ikleyn(52875)   (Show Source): (Show Source):
Question 1179802: Analyzing the functions below, compare and contrast the two functions in each problem situation. Be sure to use complete sentences in your comparison. Be sure to include a discussion of similarities and differences for the periods, amplitudes, y-minimums, y-maximums, and any phase shift between the two graphs.
1. y=3sin(2x) and y= 3cos(2x)
2. y=4sin(2x-π) and y=cos(3x- π over 2)
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's analyze the given functions and compare and contrast them:
**1. y = 3sin(2x) and y = 3cos(2x)**
* **Amplitude:** Both functions have an amplitude of 3. This means the vertical distance from the midline to the maximum or minimum value is 3.
* **Period:** Both functions have a period of π. The period is calculated as 2π / B, where B is the coefficient of x. In both cases, B = 2, so the period is 2π / 2 = π.
* **Y-Minimum:** Both functions have a y-minimum of -3.
* **Y-Maximum:** Both functions have a y-maximum of 3.
* **Phase Shift:** The two functions are related by a phase shift. Specifically, cos(x) = sin(x + π/2). Therefore:
* 3cos(2x) = 3sin(2x + π/2) = 3sin(2(x + π/4)).
* This means the cosine function is a sine function shifted π/4 units to the left.
* **Similarities:** Both functions have the same amplitude, period, y-minimum, and y-maximum. They both oscillate between -3 and 3 with a period of π.
* **Differences:** The two graphs differ only by a horizontal shift of π/4. The sine function starts at (0, 0), while the cosine function starts at (0, 3). Essentially the cosine graph is the sine graph shifted left by pi/4.
**2. y = 4sin(2x - π) and y = cos(3x - π/2)**
* **Amplitude:**
* y = 4sin(2x - π) has an amplitude of 4.
* y = cos(3x - π/2) has an amplitude of 1.
* **Period:**
* y = 4sin(2x - π) has a period of 2π / 2 = π.
* y = cos(3x - π/2) has a period of 2π / 3.
* **Y-Minimum:**
* y = 4sin(2x - π) has a y-minimum of -4.
* y = cos(3x - π/2) has a y-minimum of -1.
* **Y-Maximum:**
* y = 4sin(2x - π) has a y-maximum of 4.
* y = cos(3x - π/2) has a y-maximum of 1.
* **Phase Shift:**
* y = 4sin(2x - π) can be rewritten as 4sin(2(x - π/2)), indicating a phase shift of π/2 units to the right.
* y = cos(3x - π/2) can be rewritten as cos(3(x - π/6)), indicating a phase shift of π/6 units to the right.
* **Similarities:** Both functions represent sinusoidal curves and oscillate between their minimum and maximum values.
* **Differences:** The functions have different amplitudes, different periods, and different phase shifts.
* The sine function has a greater amplitude (4 vs 1).
* The sine function has a period of pi while the cosine has a period of 2pi/3.
* The amount of the phase shift differs as well.
Question 1181354: Prove that |z1 + z2 | < or = |z1|+|z2|. Use |z|^2 = mod z times z, Re(z) = (z + mod z)/ 2, and Re(z) < or = |z|. The inequality is known as the Triangle Inequality.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's the proof of the triangle inequality using the properties you provided:
1. **Start with the square of the absolute value:**
|z₁ + z₂|² = (z₁ + z₂)(z₁ + z₂)* (where * denotes the complex conjugate)
2. **Expand the expression:**
|z₁ + z₂|² = z₁z₁* + z₁z₂* + z₂z₁* + z₂z₂*
3. **Use the property |z|² = z * z*:**
|z₁ + z₂|² = |z₁|² + z₁z₂* + z₂z₁* + |z₂|²
4. **Rewrite the middle terms using conjugates:** Notice that z₂z₁* is the conjugate of z₁z₂*. So we can write:
z₂z₁* = (z₁z₂*)*
5. **Substitute this back into the equation:**
|z₁ + z₂|² = |z₁|² + z₁z₂* + (z₁z₂*)* + |z₂|²
6. **Use the property Re(z) = (z + z*)/2:** The middle terms can be expressed using the real part:
z₁z₂* + (z₁z₂*)* = 2 * Re(z₁z₂*)
7. **Substitute this into the equation:**
|z₁ + z₂|² = |z₁|² + 2 * Re(z₁z₂*) + |z₂|²
8. **Use the property Re(z) ≤ |z|:**
|z₁ + z₂|² ≤ |z₁|² + 2|z₁z₂*| + |z₂|²
9. **Use the property |ab| = |a||b|:**
|z₁ + z₂|² ≤ |z₁|² + 2|z₁||z₂*| + |z₂|²
10. **Since |z| = |z*|, we have:**
|z₁ + z₂|² ≤ |z₁|² + 2|z₁||z₂| + |z₂|²
11. **Recognize the perfect square:** The right side is a perfect square:
|z₁ + z₂|² ≤ (|z₁| + |z₂|)²
12. **Take the square root of both sides:** Since absolute values are non-negative, we can take the square root without changing the inequality:
|z₁ + z₂| ≤ |z₁| + |z₂|
This completes the proof of the triangle inequality.
Question 1182792: For n>_3, consider 2n points spaced regularly on a circle with alternate points black and white and a point placed at the centre of the circle.
The points are labelled -n,-n+1,...,n-1,n so that:
(a) the sum of the labels on each diameter through three of the points is a constant s, and
(b) the sum of the labels on each black-white-black triple of consecutive points on the circle is also s.
1.Show that the label on the central point is 0 and s=0. &
2.Show that such a labelling exists if and only if n is even.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to approach this problem:
**1. Showing the central point is 0 and s = 0:**
* **Central Point Label:** Let 'c' be the label of the central point. Consider any diameter passing through two points on the circle, say labeled 'i' and 'j'. According to condition (a), i + j + c = s. Now, consider the diameter perpendicular to the first one. Let the points on this diameter be labeled 'k' and 'l'. Then k + l + c = s. Since the points are spaced regularly, if i and j are at opposite ends of a diameter, so are k and l. For every point labeled 'x', there will be another point labeled '-x' on the opposite end of the diameter. So, if i and j are at opposite ends of a diameter, and k and l are at opposite ends of a diameter, then i = -j and k = -l. Therefore, i + j = 0 and k + l = 0. Therefore, 0 + c = s and 0 + c = s. This implies that c = s.
Now, consider a black-white-black triple. Let the labels be i, j, and k. Then i + j + k = s. Since the points are spaced regularly, and the labeling goes from -n to n, we know that the labels of opposite points are additive inverses of each other. For any point labeled 'x', there is a point labeled '-x' on the opposite end of the diameter.
Consider the black-white-black triple i, j, k. Because the points are spaced regularly, the point opposite to j is -j. Because the sum of diametrically opposite points is 0 and the sum of consecutive points in a black-white-black triple is s, we can deduce that the point opposite to j is -j. Since the points are spaced regularly, the point opposite to j is -j. Then i + (-j) + k = 0 (because they are on a diameter).
We also know that i + j + k = s. Subtracting the two equations, we get 2j = s.
Since we can choose any j, consider the case where j = 0. Then s = 2 * 0 = 0.
Since c = s, and s = 0, therefore c = 0.
* **Value of s:** We've shown that the label of the central point (c) is equal to s. Consider any diameter. Let the labels of the two points on the circle be 'x' and 'y'. Then x + y + c = s. Since the points are spaced regularly, we know that x = -y. Thus, x + y = 0. Therefore, 0 + c = s, which means c = s. Because c = 0, s = 0.
**2. Showing existence of labeling if and only if n is even:**
* **If n is even:** We can label the points as follows: Start at an arbitrary point and label it -n. Move clockwise and label the next point -n+1. Continue until you reach n. This labeling satisfies both conditions. The sum of labels on a diameter is -i + i + 0 = 0 = s, and the sum of a black-white-black triple is -i + i + 0 = 0 = s.
* **If n is odd:** Suppose such a labeling exists. Consider the sum of the labels of all the points on the circle. Since the points are labeled from -n to n, the sum of all the labels is 0.
Now consider the sum of all black-white-black triples. There are 2n such triples. Each point on the circle belongs to exactly two black-white-black triples.
Let the labels of the points be l_1, l_2, ..., l_{2n}.
The sum of labels of all black-white-black triples is 2(l_1 + l_2 + ... + l_{2n}) = 2 * 0 = 0.
Since the sum of each black-white-black triple is s, the sum of all black-white-black triples is 2n * s.
Therefore 2ns = 0, which means s = 0. But we know that the sum of labels on each diameter is s. Since the labels on the diameter are additive inverses, the sum of labels on each diameter is 0.
However, if n is odd, we cannot pair up all the points on the circle to form diameters because there will be one point left unpaired. This implies that the labels can't be from -n to n.
Therefore, such a labeling is impossible when n is odd.
Therefore, such a labeling exists if and only if n is even.
Question 1209595: limit x (1 - 2 cos ((pi x)/(3 x - sqrt3))) as x \[LongRightArrow] + \[Infinity]
Answer by ikleyn(52875)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In his post, @CPhill solved another problem, different from the given in the post.
For correct solution (which is very long), see the AI solution under this link
https://www.google.com/search?q=limit+x+(1+-+2+cos+((pi+x)%2F(3+x+-+sqrt3)))+as+x+%5C%5BLongRightArrow%5D+%2B+%5C%5BInfinity%5D&rlz=1C1CHBF_enUS1071US1071&oq=limit+x+(1+-+2+cos+((pi+x)%2F(3+x+-+sqrt3)))+as+x+%5C%5BLongRightArrow%5D+%2B+%5C%5BInfinity%5D&gs_lcrp=EgZjaHJvbWUyBggAEEUYOdIBCTE5NTlqMGoxNagCCLACAfEFYK947i4L-kbxBWCveO4uC_pG&sourceid=chrome&ie=UTF-8
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380
|



