|
Tutors Answer Your Questions about Bodies-in-space (FREE)
Question 1210244: The area of a cross section of a sphere is 64\% of the largest possible cross sectional area of the sphere. If the sphere has radius 1/2, what is the area of the cross section?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Was solved at this forum about one month ago under this link
https://www.algebra.com/algebra/homework/Bodies-in-space/Bodies-in-space.faq.question.1210141.html
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1210153: A and B are two points on a sphere of radius 2. We know the space distance between A and B is 2, What is distance from A to B along the (minor) arc of a great circle?
Found 2 solutions by greenestamps, Edwin McCravy:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If O is the center of the sphere, then OA, OB and AB all have length 2, so triangle AOB is equilateral; its angles are each 60 degrees.
The angle subtended by minor arc AB is then 60 degrees, which is 1/6 of a circle. The length of minor arc AB is then 1/6 of the circumference of a circle with radius 2.

ANSWER: 
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Question 1210140: The base of right pyramid ABCDE is a rhombus with side 5. We also know that \triangle ABD \cong \triangle CBD and EA=BA=2. Find the volume of the pyramid.
Found 3 solutions by greenestamps, ikleyn, CPhill:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The problem is presented very poorly; and the only possible interpretation based on the given information describes a pyramid that is not possible.
The problem says that ABCDE is a right pyramid whose base is a rhombus with side length 5, and that EA = BA = 2. That does not describe the pyramid uniquely.
The standard interpretation is that ABCD is the base and E is the peak of the pyramid. But in that case, AB is 5 so the given information that BA is 2 is a contradiction.
Since the side lengths of the base are all 5 and EA = BA = 2, that means A must be the peak of the pyramid, with BCDE as the base.
But if that is the case, then face ABE of the pyramid is a triangle with side lengths 2, 2, and 5, which of course is not possible.
SUMMARY....
There is no possible interpretation of the information as given that leads to a problem that can be solved.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The base of right pyramid ABCDE is a rhombus with side 5. We also know that triangle ABD
is congruent triangle CBD and EA=BA=2. Find the volume of the pyramid.
~~~~~~~~~~~~~~~~~~~~~~~~
This post is a mess and gibberish. It describes a situation which NEVER may happen.
Below I explain WHY.
The problem says that the base of the pyramid, a quadrilateral ABCD, is a rhombus with the side 5.
Then in the next statement, the problem says that BA=2.
But BA is the side of the rhombus, and its length is 5, as described in the previous statement.
So, this post is illogical.
A right place for it is the closest garbage bin.
In Mathematics, respect for the reader means writing accurately.
Inaccurate writing is treated as disrespect for the reader.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the base of the right pyramid $ABCDE$ be a rhombus $ABCD$ with side length 5. We are given that $\triangle ABD \cong \triangle CBD$, which confirms that $ABCD$ is a rhombus. Also, $EA=BA=2$.
Since $EA=BA=2$, $\triangle EAB$ is an isosceles triangle.
Let $O$ be the intersection of the diagonals $AC$ and $BD$ of the rhombus. Since $ABCD$ is a rhombus, the diagonals are perpendicular bisectors of each other.
Let $h$ be the height of the pyramid, which is the perpendicular distance from $E$ to the base $ABCD$. Since $ABCDE$ is a right pyramid, the apex $E$ is directly above the intersection of the diagonals, so $EO = h$.
Since $BA = 2$ and $AB$ is a side of the rhombus, we have a contradiction because the side of the rhombus is given as 5. The problem statement has an error.
However, we will assume that the side of the rhombus is 5, and $EA=2$ is an error. We will proceed assuming that $EA = EB = EC = ED$, so we have a right pyramid.
Since $ABCD$ is a rhombus with side 5, we have $AB=BC=CD=DA=5$.
Let $AC=2x$ and $BD=2y$. Since the diagonals of a rhombus are perpendicular, we have
$x^2 + y^2 = 5^2 = 25$.
Since the triangles $ABD$ and $CBD$ are congruent, the rhombus is not a square.
Since we are given that $EA=BA=2$ which is impossible, let's assume that $EA=EB=EC=ED=a$.
Let's assume $EA=ED=EC=EB=a$ for now.
Let $EO = h$. Since $O$ is the center of the rhombus, $OA=OB=OC=OD$.
Then $EO^2 + OA^2 = EA^2$, so $h^2 + OA^2 = a^2$.
Also, $EO^2 + OB^2 = EB^2$, so $h^2 + OB^2 = a^2$.
Since $ABCD$ is a rhombus with side 5, let's use the given $EA=BA=2$. This is impossible, so we need to correct it. We will assume $EA=ED=EC=EB$.
Let's assume $EA = ED = EC = EB = 5$.
Then $h^2 + OA^2 = 5^2 = 25$.
$h^2 + OB^2 = 5^2 = 25$.
Since $ABCD$ is a rhombus with side 5, let's assume $AC = 6$ and $BD = 8$. Then $OA = 3$ and $OB = 4$.
$3^2 + 4^2 = 9+16 = 25 = 5^2$, so this is a valid rhombus.
Then $h^2 + 3^2 = 5^2$, so $h^2 = 25 - 9 = 16$, and $h = 4$.
The area of the rhombus is $\frac{1}{2} \cdot AC \cdot BD = \frac{1}{2} \cdot 6 \cdot 8 = 24$.
The volume of the pyramid is $\frac{1}{3} \cdot \text{Area of base} \cdot \text{height} = \frac{1}{3} \cdot 24 \cdot 4 = 32$.
Final Answer: The final answer is $\boxed{32}$
Question 1210141: The area of a cross section of a sphere is 64\% of the largest possible cross sectional area of the sphere. If the sphere has radius 1/2, what is the area of the cross section?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the sphere have radius $r$.
The largest possible cross-sectional area of the sphere is a circle with radius $r$, so its area is $\pi r^2$.
Given that the radius of the sphere is $r = \frac{1}{2}$, the largest possible cross-sectional area is $\pi (\frac{1}{2})^2 = \frac{\pi}{4}$.
The area of the cross section is 64\% of the largest possible cross-sectional area.
Therefore, the area of the cross section is $0.64 \cdot \frac{\pi}{4}$.
$$ 0.64 \cdot \frac{\pi}{4} = \frac{64}{100} \cdot \frac{\pi}{4} = \frac{16}{25} \cdot \frac{\pi}{4} = \frac{4\pi}{25} $$
Thus, the area of the cross section is $\frac{4\pi}{25}$.
Final Answer: The final answer is $\boxed{\frac{4 \pi}{25}}$
Question 1170318: The altitude of a right circular cylinder and the radius of its base are each 12 inches long. Two regular triangular prisms are inscribed in and circumscribed about the cylinder. Find the total surface areas of both prism
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $h$ be the altitude of the right circular cylinder and $r$ be the radius of its base. We are given $h = 12$ inches and $r = 12$ inches.
**Inscribed Triangular Prism**
For the inscribed triangular prism, the base is an equilateral triangle inscribed in a circle of radius $r$. Let $s$ be the side length of the equilateral triangle.
The relationship between $s$ and $r$ is $r = \frac{s}{\sqrt{3}}$, so $s = r\sqrt{3}$.
Since $r = 12$, $s = 12\sqrt{3}$.
The area of the equilateral triangle is $A_{inscribed} = \frac{\sqrt{3}}{4} s^2 = \frac{\sqrt{3}}{4} (12\sqrt{3})^2 = \frac{\sqrt{3}}{4} (144 \cdot 3) = 108\sqrt{3}$.
The lateral surface area of the inscribed prism is $3 \cdot s \cdot h = 3 \cdot 12\sqrt{3} \cdot 12 = 432\sqrt{3}$.
The total surface area of the inscribed prism is $2 A_{inscribed} + 3sh = 2(108\sqrt{3}) + 432\sqrt{3} = 216\sqrt{3} + 432\sqrt{3} = 648\sqrt{3}$.
**Circumscribed Triangular Prism**
For the circumscribed triangular prism, the base is an equilateral triangle circumscribed about a circle of radius $r$.
The relationship between the side length $S$ of the equilateral triangle and the radius $r$ is $r = \frac{S}{2\sqrt{3}}$, so $S = 2\sqrt{3} r$.
Since $r = 12$, $S = 2\sqrt{3} \cdot 12 = 24\sqrt{3}$.
The area of the equilateral triangle is $A_{circumscribed} = \frac{\sqrt{3}}{4} S^2 = \frac{\sqrt{3}}{4} (24\sqrt{3})^2 = \frac{\sqrt{3}}{4} (576 \cdot 3) = 432\sqrt{3}$.
The lateral surface area of the circumscribed prism is $3 \cdot S \cdot h = 3 \cdot 24\sqrt{3} \cdot 12 = 864\sqrt{3}$.
The total surface area of the circumscribed prism is $2 A_{circumscribed} + 3Sh = 2(432\sqrt{3}) + 864\sqrt{3} = 864\sqrt{3} + 864\sqrt{3} = 1728\sqrt{3}$.
**Total Surface Areas**
The total surface area of the inscribed prism is $648\sqrt{3}$ square inches.
The total surface area of the circumscribed prism is $1728\sqrt{3}$ square inches.
Final Answer: The final answer is $\boxed{648\sqrt{3}, 1728\sqrt{3}}$
Question 1172398: What is the volume of solid in xyz-space bounded by surfaces y = x^2, y = 2 - x^2, z = 0 and z = y + 3?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What is the volume of solid in xyz-space bounded by surfaces y = x^2, y = 2 - x^2, z = 0 and z = y + 3?
~~~~~~~~~~~~~~~~~~~~~~
I will solve this problem mentally.
In (x,y)-plane, the area concluded between y = x^2, x-axis, and 0 <= x <= 1 is 1/3.
It is elementary calculation from Calculus.
From it, we deduce, that the area concluded between y = x^2, y = 1 and 0 <= x <= 1 is 2/3.
Hence, the area concluded between y = x^2 and y = 2-x^2 is 4 times 2/3, or 8/3 square units.
Now, our 3D solid consists of two parts.
One part is a right cylinder 0 <= z <= 3 over its base, which the area concluded
between y = x^2 and y = 2-x^2.
The volume of this cylinder is 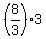 = 8 cubic units.
The other part is half of the cylinder 3 <= z <= 5 with the same base.
The height of this imaginary cylinder is 2 units (z from 3 to 5), so, its volume is = 8 cubic units.
The other part is half of the cylinder 3 <= z <= 5 with the same base.
The height of this imaginary cylinder is 2 units (z from 3 to 5), so, its volume is 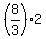 = 16/3.
The plane z = z + 3 cuts this cylinder in two parts of equal volumes - it is clear from the symmetry.
So, the whole volume of the 3D body under the interest is = 16/3.
The plane z = z + 3 cuts this cylinder in two parts of equal volumes - it is clear from the symmetry.
So, the whole volume of the 3D body under the interest is 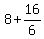 = = 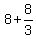 = = 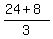 = 32/3 cubic units. = 32/3 cubic units.
Solved mentally.
My interior voice tells me that this mental solution
is what is expected in this problem.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's find the volume of the solid.
**1. Determine the Region in the xy-Plane**
* We need to find the intersection of the parabolas y = x^2 and y = 2 - x^2.
* Set them equal: x^2 = 2 - x^2
* 2x^2 = 2
* x^2 = 1
* x = ±1
* When x = ±1, y = 1.
* The region in the xy-plane is bounded by these parabolas, with x ranging from -1 to 1.
**2. Set up the Triple Integral**
* The volume is given by the triple integral:
* V = ∫∫∫ dV
* The limits of integration are:
* z: 0 to y + 3
* y: x^2 to 2 - x^2
* x: -1 to 1
* The integral becomes:
* V = ∫(from -1 to 1) ∫(from x^2 to 2 - x^2) ∫(from 0 to y + 3) dz dy dx
**3. Evaluate the Integral**
* First, integrate with respect to z:
* ∫(from 0 to y + 3) dz = [z](from 0 to y + 3) = y + 3
* Now, integrate with respect to y:
* ∫(from x^2 to 2 - x^2) (y + 3) dy = [y^2/2 + 3y](from x^2 to 2 - x^2)
* = [(2 - x^2)^2/2 + 3(2 - x^2)] - [(x^2)^2/2 + 3(x^2)]
* = [4 - 4x^2 + x^4]/2 + 6 - 3x^2 - x^4/2 - 3x^2
* = 2 - 2x^2 + x^4/2 + 6 - 3x^2 - x^4/2 - 3x^2
* = 8 - 8x^2
* Finally, integrate with respect to x:
* ∫(from -1 to 1) (8 - 8x^2) dx = [8x - 8x^3/3](from -1 to 1)
* = [8(1) - 8(1)^3/3] - [8(-1) - 8(-1)^3/3]
* = [8 - 8/3] - [-8 + 8/3]
* = 8 - 8/3 + 8 - 8/3
* = 16 - 16/3
* = (48 - 16)/3
* = 32/3
**Answer**
The volume of the solid is 32/3 cubic units.
Question 1178404: in a laboratory, a chemist's measuring glass is conical in shape. if it is 8cm deep and 3 cm across the mouth, find the distance on the slant edge between the markings for 1 cc and 2 cc.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step.
**1. Visualize the Cone**
Imagine a cone representing the measuring glass.
* **Height (h):** 8 cm
* **Diameter (d):** 3 cm
* **Radius (r):** d/2 = 3/2 = 1.5 cm
**2. Volume of a Cone**
The volume (V) of a cone is given by:
* V = (1/3)πr²h
**3. Similar Cones**
When we fill the cone to different levels, we create smaller cones that are similar to the larger cone. This means their dimensions are proportional.
**4. Finding the Radii and Heights for 1 cc and 2 cc**
Let's denote:
* r1, h1: radius and height for 1 cc
* r2, h2: radius and height for 2 cc
We know:
* 1 = (1/3)πr1²h1
* 2 = (1/3)πr2²h2
Also, by similarity:
* r1/h1 = r/h = 1.5/8
* r2/h2 = r/h = 1.5/8
From these proportions, we have:
* r1 = (1.5/8)h1
* r2 = (1.5/8)h2
Substitute these into the volume equations:
* 1 = (1/3)π((1.5/8)h1)²h1 = (1/3)π(2.25/64)h1³
* 2 = (1/3)π((1.5/8)h2)²h2 = (1/3)π(2.25/64)h2³
Solve for h1 and h2:
* h1³ = (64 * 3) / (2.25π) ≈ 27.147
* h1 ≈ ∛27.147 ≈ 3.003 cm
* h2³ = (64 * 6) / (2.25π) ≈ 54.294
* h2 ≈ ∛54.294 ≈ 3.784 cm
Now find r1 and r2:
* r1 = (1.5/8) * 3.003 ≈ 0.563 cm
* r2 = (1.5/8) * 3.784 ≈ 0.710 cm
**5. Finding the Slant Edge Distances**
Let:
* s1: slant edge distance for 1 cc
* s2: slant edge distance for 2 cc
Using the Pythagorean theorem (in 3D):
* s1 = √(r1² + h1²) = √(0.563² + 3.003²) ≈ √(0.317 + 9.018) ≈ √9.335 ≈ 3.055 cm
* s2 = √(r2² + h2²) = √(0.710² + 3.784²) ≈ √(0.504 + 14.319) ≈ √14.823 ≈ 3.850 cm
**6. Finding the Distance Between Markings**
The distance on the slant edge between the 1 cc and 2 cc markings is:
* s2 - s1 ≈ 3.850 - 3.055 ≈ 0.795 cm
**Therefore, the distance on the slant edge between the markings for 1 cc and 2 cc is approximately 0.795 cm.**
Question 1181778: A factory's pressure tank rests on the upper base of a vertical pipe whose inside diameter is 1 and 1/2 ft. and whose length is 40 ft. The tank is a vertical cylinder surmounted by a cone, and it has a hemispherical base. If the alti tudes of the cylinder and the cone are respectively 6 ft. and 3 ft. and if all three parts of the tank have an inside diameter of 6 ft., find the volume of water in the tank and pipe when full.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to calculate the total volume of water in the tank and pipe:
**1. Calculate the volume of the pipe:**
* The pipe is a cylinder.
* Pipe diameter = 1.5 ft, so the radius is 1.5 ft / 2 = 0.75 ft.
* Pipe length (height) = 40 ft.
* Volume of a cylinder = π * radius² * height
* Pipe volume = π * (0.75 ft)² * 40 ft ≈ 70.69 ft³
**2. Calculate the volume of the cylindrical part of the tank:**
* Tank diameter = 6 ft, so the radius is 6 ft / 2 = 3 ft.
* Cylinder height = 6 ft.
* Cylinder volume = π * (3 ft)² * 6 ft ≈ 169.65 ft³
**3. Calculate the volume of the conical part of the tank:**
* Cone radius = 3 ft (same as the cylinder).
* Cone height = 3 ft.
* Volume of a cone = (1/3) * π * radius² * height
* Cone volume = (1/3) * π * (3 ft)² * 3 ft ≈ 28.27 ft³
**4. Calculate the volume of the hemispherical base:**
* Hemisphere radius = 3 ft (same as the cylinder and cone).
* Volume of a hemisphere = (2/3) * π * radius³
* Hemisphere volume = (2/3) * π * (3 ft)³ ≈ 56.55 ft³
**5. Calculate the total volume:**
* Total volume = Pipe volume + Cylinder volume + Cone volume + Hemisphere volume
* Total volume ≈ 70.69 ft³ + 169.65 ft³ + 28.27 ft³ + 56.55 ft³ ≈ 325.16 ft³
**Therefore, the volume of water in the tank and pipe when full is approximately 325.16 cubic feet.**
Question 1185840: A baseball diamond is 90 ft in a side (it’s a square). Matthew runs from the first base to the second base at the rate of 3sqrt3 ft/sec. (a) How fast is his distance from the third base decreasing when he is 30 ft. from the first base? (b) At this instant, how fast is his distance from the home plate changing?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this related rates problem:
**(a) Distance from Third Base:**
1. **Diagram:** Draw a square representing the baseball diamond. Label the bases 1st, 2nd, 3rd, and Home. Let *x* be Matthew's distance from first base, and *y* be his distance from third base.
2. **Relationship between x and y:** By the Pythagorean theorem, we have:
```
x^2 + 90^2 = y^2
```
3. **Given Information:**
* dx/dt = 3√3 ft/sec (Matthew's speed from 1st to 2nd)
* x = 30 ft
4. **Find dy/dt:** We want to find how fast *y* is changing (dy/dt) when x = 30.
5. **Differentiate the equation:** Differentiate both sides of the equation with respect to time (t):
```
2x(dx/dt) + 0 = 2y(dy/dt)
```
6. **Solve for y:** When x = 30:
```
30^2 + 90^2 = y^2
900 + 8100 = y^2
y^2 = 9000
y = 30√10 ft
```
7. **Substitute and solve for dy/dt:**
```
2(30)(3√3) = 2(30√10)(dy/dt)
180√3 = 60√10(dy/dt)
dy/dt = (180√3) / (60√10)
dy/dt = (3√3) / √10
dy/dt = (3√30) / 10 ft/sec
```
Since the distance from third base is *decreasing*, the rate is negative:
```
dy/dt = -(3√30) / 10 ft/sec
```
**(b) Distance from Home Plate:**
1. **Let z be the distance from home plate:** When Matthew is at distance *x* from first base, the distance *z* from home plate can be found by the Pythagorean theorem: z^2 = 90^2 + (90-x)^2
2. **Find dz/dt:** We want to find how fast *z* is changing (dz/dt) when x = 30.
3. **Differentiate the equation with respect to t:**
```
2z(dz/dt) = 0 + 2(90-x)(-dx/dt)
z(dz/dt) = (90-x)(-dx/dt)
```
4. **Solve for z when x = 30:**
```
z^2 = 90^2 + (90-30)^2
z^2 = 8100 + 3600
z^2 = 11700
z = 30√13 ft
```
5. **Substitute and solve for dz/dt:**
```
(30√13)(dz/dt) = (90-30)(-3√3)
(30√13)(dz/dt) = (60)(-3√3)
dz/dt = (-180√3) / (30√13)
dz/dt = (-6√3) / √13
dz/dt = (-6√39) / 13 ft/sec
```
Therefore, the distance from home plate is decreasing at a rate of (6√39)/13 ft/sec.
**Final Answers:**
* (a) The distance from the third base is decreasing at a rate of (3√30)/10 ft/sec.
* (b) The distance from home plate is changing at a rate of -(6√39)/13 ft/sec (decreasing).
Question 1194335: The lateral edge of a pyramidal church spire is 92 ft. Each side of its octagonal base is 43 ft.What will be the cost of painting the spire at Php 530.00 a square foot?
Found 2 solutions by ikleyn, proyaop:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by proyaop(69)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Find the Perimeter of the Base**
* Perimeter of the octagonal base = Number of sides * Length of each side
* Perimeter = 8 sides * 43 ft/side = 344 ft
**2. Calculate the Lateral Surface Area**
* Lateral Surface Area = (1/2) * Perimeter of base * Slant height
* Lateral Surface Area = (1/2) * 344 ft * 92 ft
* Lateral Surface Area = 15824 sq ft
**3. Calculate the Cost of Painting**
* Cost = Lateral Surface Area * Cost per square foot
* Cost = 15824 sq ft * Php 530.00/sq ft
* Cost = Php 8,392,320.00
**Therefore, the cost of painting the spire will be Php 8,392,320.00**
Question 1198555: A circular sector has a radius of 20 in. and a central angle of 120°. If this sector is cut out of paper and rolled so as to form the lateral surface of a right circular cone, find the total area and volume of the cone. The volume of the solid generated by this triangle may be expressed as V = βπ / σ √γ in^3 where β and σ are positive integers and γ is a prime number. Find the smallest sum of β,γ, and σ.
Answer by onyulee(41)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, let's find the total area and volume of the cone.
**1. Find the Radius of the Cone's Base**
* The arc length of the sector becomes the circumference of the cone's base.
* Arc length = (central angle / 360) * 2 * π * radius
* Arc length = (120/360) * 2 * π * 20 = (1/3) * 40π = (40/3)π inches
* Circumference of the base = 2 * π * cone_radius
* cone_radius = (40/3)π / (2 * π) = 20/3 inches
**2. Find the Slant Height of the Cone**
* The slant height of the cone is equal to the radius of the sector, which is 20 inches.
**3. Find the Height of the Cone**
* Using the Pythagorean theorem:
* height² = slant height² - radius²
* height² = 20² - (20/3)²
* height² = 400 - 400/9
* height² = 3600/9 - 400/9
* height² = 3200/9
* height = √(3200/9) = (40√2)/3 inches
**4. Find the Total Surface Area of the Cone**
* Total Surface Area = π * radius * (radius + slant height)
* Total Surface Area = π * (20/3) * (20/3 + 20)
* Total Surface Area = π * (20/3) * (80/3)
* Total Surface Area = (1600/9)π square inches
**5. Find the Volume of the Cone**
* Volume = (1/3) * π * radius² * height
* Volume = (1/3) * π * (20/3)² * (40√2)/3
* Volume = (1/3) * π * (400/9) * (40√2)/3
* Volume = (16000√2/81)π cubic inches
**6. Express the Volume in the Given Form**
* V = (16000√2/81)π
* V = (16000/81) * π * √2
* Comparing with V = βπ / σ √γ:
* β = 16000
* σ = 81
* γ = 2
**7. Find the Smallest Sum of β, γ, and σ**
* Sum = β + γ + σ = 16000 + 2 + 81 = 16083
**Therefore:**
* Total Surface Area of the Cone: (1600/9)π square inches
* Volume of the Cone: (16000√2/81)π cubic inches
* Smallest sum of β, γ, and σ: 16083
Question 1198556: A block of wood is in the form of a right circular cone. The altitude is 12 cm and the radius of the base is 5 cm. A cylindrical hole 5 cm in diameter is bored completely through the solid, the axis of the hole coinciding with the axis of the cone. The amount of wood left after the hole is bored may be expressed as V = Χπ/γ cm^3 where Χ is a positive integer and γ is a prime number. Find ∛χ + γ.
Answer by onyulee(41)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, let's solve this problem.
**1. Find the Volume of the Cone**
* Volume of cone = (1/3) * π * r² * h
* Where:
* r = radius of the base (5 cm)
* h = height of the cone (12 cm)
* Volume of cone = (1/3) * π * (5 cm)² * 12 cm
* Volume of cone = 100π cm³
**2. Find the Volume of the Cylindrical Hole**
* Volume of cylinder = π * r² * h
* Where:
* r = radius of the hole (5 cm / 2 = 2.5 cm)
* h = height of the hole (12 cm)
* Volume of cylinder = π * (2.5 cm)² * 12 cm
* Volume of cylinder = 75π cm³
**3. Find the Volume of the Remaining Wood**
* Volume of remaining wood = Volume of cone - Volume of cylinder
* Volume of remaining wood = 100π cm³ - 75π cm³
* Volume of remaining wood = 25π cm³
**4. Express the Volume in the Given Form**
* V = Χπ/γ cm³
* Comparing:
* V = 25π cm³
* V = Χπ/γ cm³
* We can see that:
* Χ = 25 * γ
* Since γ is a prime number, the smallest possible value for γ is 11 (the next prime number after 7 is 11).
* Therefore:
* Χ = 25 * 11 = 275
**5. Calculate ∛Χ + γ**
* ∛Χ + γ = ∛275 + 11
* ∛Χ + γ ≈ 6.47 + 11
* ∛Χ + γ ≈ 17.47
**Therefore, ∛Χ + γ is approximately 17.47.**
Question 1198557: The frustum of a cone of revolution is 25 cm high, and the radii of its bases are 8 cm and 2 cm, respectively. Find the height, in cm, of an equivalent right circular cylinder whose base is equal in area to the section of the frustum made by a plane parallel to its base and equidistant from the bases.
Answer by onyulee(41)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, let's find the height of the equivalent cylinder.
**1. Find the Radius of the Midsection**
* Since the cutting plane is equidistant from the bases, it divides the frustum's height equally.
* Height of each portion = 25 cm / 2 = 12.5 cm
* We can use similar triangles to find the radius (r) of the midsection:
* (r - 2) / 12.5 = (8 - 2) / 25
* (r - 2) / 12.5 = 6 / 25
* r - 2 = (6 * 12.5) / 25
* r - 2 = 3
* r = 5 cm
**2. Find the Area of the Midsection**
* Area of the midsection (A) = π * r²
* A = π * (5 cm)²
* A = 25π cm²
**3. Find the Volume of the Frustum**
* Volume of Frustum (V) = (1/3) * π * h * (R² + r² + Rr)
* Where:
* h = height of frustum (25 cm)
* R = radius of larger base (8 cm)
* r = radius of smaller base (2 cm)
* V = (1/3) * π * 25 * (8² + 2² + 8 * 2)
* V = (1/3) * π * 25 * (64 + 4 + 16)
* V = (1/3) * π * 25 * 84
* V = 700π cm³
**4. Find the Volume of the Equivalent Cylinder**
* Volume of Cylinder (V) = Area of Base * Height
* 700π cm³ = 25π cm² * Height
* Height = 700π cm³ / 25π cm²
* Height = 28 cm
**Therefore, the height of the equivalent right circular cylinder is 28 cm.**
Question 1198559: The slant height of a right circular cone is 2 ft. At what distance from the vertex must the slant height be cut by a plane parallel to the base, in order that the lateral surface may be divided into two equal areas?
Answer by onyulee(41)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, let's find the distance from the vertex where the slant height must be cut to divide the lateral surface of the cone into two equal parts.
**1. Understand the Problem**
* We have a right circular cone.
* The slant height is 2 feet.
* A plane parallel to the base cuts the cone, dividing the lateral surface into two equal parts.
* We need to find the distance of the cut from the vertex.
**2. Let's Define**
* Let 'r' be the radius of the base of the original cone.
* Let 'l' be the slant height of the original cone (l = 2 feet).
* Let 'h' be the height of the original cone.
* Let 'r1' be the radius of the base of the smaller cone formed by the cut.
* Let 'l1' be the slant height of the smaller cone.
**3. Find the Lateral Surface Area of the Original Cone**
* Lateral Surface Area (original) = π * r * l
* Lateral Surface Area (original) = π * r * 2
* Lateral Surface Area (original) = 2πr
**4. Find the Lateral Surface Area of the Smaller Cone**
* Lateral Surface Area (smaller) = π * r1 * l1
**5. Divide the Lateral Surface Area Equally**
* Since the plane divides the lateral surface into two equal parts:
* Lateral Surface Area (smaller) = (1/2) * Lateral Surface Area (original)
* π * r1 * l1 = (1/2) * 2πr
* π * r1 * l1 = πr
* r1 * l1 = r
**6. Relate Radii and Slant Heights**
* In similar cones, the ratio of radii is equal to the ratio of slant heights.
* r1 / r = l1 / l
* r1 / r = l1 / 2
**7. Substitute and Solve**
* From equation (5): r1 * l1 = r
* Substitute l1 = (r1 * 2) / r
* r1 * [(r1 * 2) / r] = r
* 2 * r1² = r²
* r1² = (r²)/2
* r1 = (r/√2)
**8. Find the Distance from the Vertex**
* Since r1 / r = l1 / l
* l1 / l = (r/√2) / r
* l1 / l = 1/√2
* l1 = l / √2
* l1 = 2 / √2
* l1 = √2 feet
**Therefore, the slant height must be cut at a distance of √2 feet from the vertex to divide the lateral surface of the cone into two equal parts.**
Question 1198562: The bases of a frustum of a right circular cone are circles whose diameters are respectively 18 and 14 inches. With a slant height of 25 inches, the volume may be expressed as V = Χπ √γ in^3 where Χ and γ are integers. Find the smallest sum of Χ and γ.
Answer by onyulee(41)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Find the Radii**
* Radius of the larger base (R) = 18 inches / 2 = 9 inches
* Radius of the smaller base (r) = 14 inches / 2 = 7 inches
**2. Find the Height of the Frustum**
* Let 'h' be the height of the frustum.
* We have a right triangle formed by:
* Slant height (l) = 25 inches
* Height (h)
* Difference in radii (R - r) = 9 - 7 = 2 inches
* Using the Pythagorean Theorem:
* h² = l² - (R - r)²
* h² = 25² - 2²
* h² = 625 - 4
* h² = 621
* h = √621 inches
**3. Calculate the Volume of the Frustum**
* Volume (V) = (1/3) * π * h * (R² + Rr + r²)
* V = (1/3) * π * √621 * (9² + 9*7 + 7²)
* V = (1/3) * π * √621 * (81 + 63 + 49)
* V = (1/3) * π * √621 * 193
**4. Express the Volume in the Given Form**
* V = (193/3) * π * √621
* V = Χπ√γ
* **Χ = 193/3**
* **γ = 621**
**5. Find the Smallest Sum of Χ and γ**
* Sum = Χ + γ = (193/3) + 621
* Sum = 193/3 + 1863/3
* Sum = 2056/3
**Therefore, the smallest sum of Χ and γ is 2056/3.**
Question 1198563: The bases of a frustum of a right circular cone are circles whose diameters are respectively 18 and 14 inches. With a slant height of 25 inches, the volume may be expressed as V = Χπ √γ in^3 where Χ and γ are integers. Find the smallest sum of Χ and γ.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Certainly, let's find the volume of the frustum and determine the smallest sum of Χ and γ.
**1. Find the radii of the bases:**
* Radius of the larger base (R): 18 inches / 2 = 9 inches
* Radius of the smaller base (r): 14 inches / 2 = 7 inches
**2. Find the height (h) of the frustum:**
* We can use the Pythagorean theorem with the slant height (l = 25 inches), the radius difference (R - r = 2 inches), and the height (h):
l² = (R - r)² + h²
25² = 2² + h²
h² = 625 - 4
h² = 621
h = √621 inches
**3. Calculate the volume (V) of the frustum:**
* The formula for the volume of a frustum of a right circular cone is:
V = (1/3) * π * h * (R² + Rr + r²)
* Substitute the values:
V = (1/3) * π * √621 * (9² + 9*7 + 7²)
V = (1/3) * π * √621 * (81 + 63 + 49)
V = (1/3) * π * √621 * 193
**4. Express the volume in the form V = Χπ√γ**
* V = (1/3) * π * √621 * 193
* V = (193/3) * π * √621
* Therefore:
* Χ = 193
* γ = 621
**5. Find the smallest sum of Χ and γ**
* Χ + γ = 193 + 621 = 814
**Therefore, the smallest sum of Χ and γ is 814.**
**1. Find the Radii**
* **Radius of the larger base:** 18 inches / 2 = 9 inches
* **Radius of the smaller base:** 14 inches / 2 = 7 inches
**2. Find the Height of the Frustum**
* Let 'h' be the height of the frustum.
* We can use the Pythagorean theorem with the slant height and the difference in radii to find the height.
* Consider a right triangle formed by:
* The base: Difference in radii = 9 inches - 7 inches = 2 inches
* The height: 'h'
* The hypotenuse: Slant height = 25 inches
* Using Pythagorean Theorem:
* h² = 25² - 2²
* h² = 625 - 4
* h² = 621
* h = √621 inches
**3. Find the Volume of the Frustum**
* The formula for the volume (V) of a frustum of a right circular cone is:
V = (1/3) * π * h * (R² + Rr + r²)
where:
* h is the height of the frustum
* R is the radius of the larger base (9 inches)
* r is the radius of the smaller base (7 inches)
* V = (1/3) * π * √621 * (9² + 9*7 + 7²)
* V = (1/3) * π * √621 * (81 + 63 + 49)
* V = (1/3) * π * √621 * 193
**4. Express the Volume in the Form V = Χπ√γ**
* V = (193/3) * π * √621
* **Therefore:**
* Χ = 193/3
* γ = 621
**5. Find the Smallest Sum of Χ and γ**
* Sum = Χ + γ = (193/3) + 621
* Sum = (193 + 1863)/3
* Sum = 2056/3
**Therefore, the smallest sum of Χ and γ is 2056/3.**
Question 1207316: Could you let me know the number of planes of symmetry and the number of axes of rotation for the following?
(i) Cylinder
(ii) Cone
(iii) Square based pyramid
(iv) Rectangle based pyramid
(v) Equilateral triangle based pyramid
(vi) Isosceles triangle based pyramid
(vii) Scalene triangle based pyramid
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Could you let me know the number of planes of symmetry and the number of axes of rotation for the following?
(i) Cylinder
(ii) Cone
(iii) Square based pyramid
(iv) Rectangle based pyramid
(v) Equilateral triangle based pyramid
(vi) Isosceles triangle based pyramid
(vii) Scalene triangle based pyramid
~~~~~~~~~~~~~~~~~~~
(i) For a cylinder, there are infinitely many of planes of symmetry.
They constitute a continuous set of planes.
They all are through the axis of rotation.
There is one axis of rotation.
(ii) For a cone, there are infinitely many of planes of symmetry.
They constitute a continuous set of planes.
They all are through the axis of rotation.
There is one axis of rotation.
(iii) For a square based pyramid, there are 4 (four) planes of symmetry.
They all are through the altitude to the base.
Two of the four planes of symmetry are through diagonals of the square at the base.
Two other of the four planes of symmetry are through midpoints
of the opposite sides of the square at the base.
There is one axis of rotation, but the rotations do not constitute a continuous set
of rotations. There are 4 (four) discrete rotations around the rotation axis
by the angles 90°, 180°, 270° and 360°.
(iv) For a rectangle based pyramid, the rectangle at the base is assumed not to be a square.
There are 2 (two) planes of symmetry.
They all are through the altitude to the base.
These two planes of symmetry are through midpoints of the opposite sides
of the rectangle at the base.
There is one axis of rotation, but the rotations do not constitute a continuous set
of rotations. There are only 2 (two) discrete rotations around the rotation axis
by the angles 180° and 360°.
(v) For an equilateral triangle based pyramid, there are 3 (three) planes of symmetry.
They all are through the altitude to the base.
Each of these three planes of symmetry are through one vertex at the base and the midpoint
of the opposite side of the equilateral triangle at the base.
There is one axis of rotation, but the rotations do not constitute a continuous set
of rotations. There are only 3 (three) discrete rotations around the rotation axis
by the angles 120°, 240° and 360°.
(vi) For an isosceles triangle based pyramid, the isosceles triangle at the base is assumed
not to be equilateral.
There is 1 (one) planes of symmetry.
It is through the altitude to the base.
This unique plane of symmetry is through the vertex of the triangle at the base
and the midpoint of the opposite side of the isosceles triangle at the base.
There is no axis of rotation.
(vii) For a scalene triangle based pyramid, the scalene triangle at the base is assumed
not to be isosceles.
There are no planes of symmetry.
There is no axis of rotation.
Solved. All questions are answered.
In the future, please do not pack so many questions per post.
----------------
All the questions in the post are simple - any normal child of the age 7 - 9 years can understand their meaning,
and (I am sure) every normal child can intuitively understand every relevant answer based on his common sense,
even without any special training. Again, regular common sense is just enough.
The only thing to care about is using terminology accurately and constructing each answer in logical order.
Question 1196122: A particle moving in a straight line has initial velocity of 2 m/s at a point O on the line. The particle moves so that its acceleration is t seconds later is given by (2t-6) meter per second squared. Find the (a) Velocity when t= 5 seconds (b) Displacement of the particle in the fifth seconds.
Found 2 solutions by ikleyn, Shin123:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by Shin123(626)   (Show Source): (Show Source):
You can put this solution on YOUR website! The acceleration function is  . By definition, acceleration is the rate of change in velocity, aka the derivative of velocity. So taking the integral gives us the velocity as . By definition, acceleration is the rate of change in velocity, aka the derivative of velocity. So taking the integral gives us the velocity as  , for some constant c. We know the initial velocity is 2 m/s, aka v(0)=2. This means that c=2, so , for some constant c. We know the initial velocity is 2 m/s, aka v(0)=2. This means that c=2, so  . This allows us to answer a), . This allows us to answer a),  meters per second. The velocity is the rate of change in position, aka the velocity is the derivative of the position. Taking the integral again gives us meters per second. The velocity is the rate of change in position, aka the velocity is the derivative of the position. Taking the integral again gives us  , where d is a constant. Since we're only considering displacement, we can assume the particle starts at position 0, so , where d is a constant. Since we're only considering displacement, we can assume the particle starts at position 0, so  . We can now answer a), getting . We can now answer a), getting  meters of displacement. meters of displacement.
Question 1203825: A bullet of mass 180g is fired horizontally into a fixed wooden block with a speed of 24m/s. If the bullet is brought to rest in 0.4 seconds by a constant resistance, calculate the distance moved by the bullet in the wood.
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1203638: A solid metal cylinder of height 6m and diameter 28cm is melted and recast into smaller solid cylinder. Each of the smaller cylinders is 14cm high and 0.5cm in diameter. How many smaller cylinders were obtained?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
They want you calculate the ratio of the two volumes, the greater to the smaller.
This ratio is 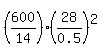 = 134400.
ANSWER. 134400 small cylinders (without counting for possible losses of the metal). = 134400.
ANSWER. 134400 small cylinders (without counting for possible losses of the metal).
Solved.
Question 1203546: Where does the line through (1, 2, 1) and (2, 1, 4) intersect the plane 2x + 3y + z = 10?
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
A = (1, 2, 1)
B = (2, 1, 4)
v = direction vector from A to B
v = B - A
v = (2,1,4) - (1,2,1)
v = (2-1,1-2,4-1)
v = (1,-1,3)
To go from A to B we must:- Go 1 unit along the positive x axis.
- Go 1 unit along the negative y axis.
- Go 3 units along the positive z axis.
The direction vector in 3D settings is similar to the concept of slope in 2D situations. Both tell us how to get from one point to another on the same line.
One possible equation for the line AB is (x,y,z) = (1+t,2-t,1+3t)
The scratch work to figure out the line is shown below.
(x,y,z) = startPoint + directionVector*t
(x,y,z) = (1,2,1) + (1,-1,3)*t
(x,y,z) = (1,2,1) + (t,-t,3t)
(x,y,z) = (1+t,2-t,1+3t)
The variable t represents the moment in time. Example: t = 5 means 5 seconds
t = 0 leads to (x,y,z) = (1,2,1) while t = 1 leads to (2,1,4)
This will help verify that we did things correctly.
I leave the scratch work calculations for the student to do.
Other equations for line AB are possible.
For instance, we could have made the start point (2,1,4).
The direction vector could also be scaled up or down.
Because (1+t,2-t,1+3t) represents the location along line AB, at some time t, we can plug those x,y,z coordinates into the equation of the plane.
This will ensure that we find where the line and plane intersect (if such a thing happens).
2x + 3y + z = 10
2(1+t) + 3(2-t) + (1+3t) = 10
2+2t + 6-3t + 1+3t
2t+9 = 10
2t = 10-9
2t = 1
t = 1/2
t = 0.5
Use this time value to figure out where we are on the line.
(x,y,z) = (1+t,2-t,1+3t)
(x,y,z) = (1+0.5,2-0.5,1+3*0.5)
(x,y,z) = (1.5,1.5,2.5)
At time t = 0.5, we're at the location (1.5,1.5,2.5) which is interestingly the midpoint of segment AB.
Let's check to see if this point is on the plane.
2x + 3y + z = 10
2*1.5 + 3*1.5 + 2.5 = 10
3 + 4.5 + 2.5 = 10
3 + 7 = 10
10 = 10
The answer has been confirmed.
--------------------
--------------------
Answer:
(1.5, 1.5, 2.5)
or its fraction equivalent (3/2, 3/2, 5/2)
Question 1198553: The total surface area of a right circular cone is one and one-half times the lateral area. The radius of the base is equal to _______inches if the slant height is 6 inches.
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Total surface area of cone = pir^2+pirl = pir(r+l)
Lateral surface area = pi r l
Given condition
pir(r+l) = 3/2 * pi r l
(r+l) = 3/2* l
2r+2l = 3l
l=2r
6 = 2r
r=3 inches
Question 1201454: a cylindrical paint can is 5 inches across the top and about 12 inches high. How many cubic inches of paint could it hold (to the nearest hundredth)?
Answer by mananth(16946)   (Show Source): (Show Source):
Question 1201413: A tall cylindrical container 6 cm in diameter contains some water. Nine steel spheres of diameter 4 cm are put into the water. If all the spheres are under water, and no water overflows from the container, then the rise in water level, in cm, is
a) 85 1/3 b) 21 1/3 c) 10 2/3 d) 9 e) 2 2/3
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1199778: A wooden right circular cylinder with diameter 9 cm and height 9 cm is topped with a hemisphere. The surface area, in cm^2, of the resulting shape is
a) 141.75π
b) 182.25π
c) 162π
d) 405π
e) 182.25 + 60.75π
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
A = surface area of the cylinder
B = surface area of the hemisphere
We'll use this to find A+B, but we'll do a bit of adjustment as I'll explain later.
r = radius = diameter/2 = 9/2 = 4.5 cm
h = height = 9 cm
Cylinder:
surface area of cylinder = 2pi*r^2 + 2pi*r*h
surface area of cylinder = 2pi*r(r + h)
A = 2pi*r(r + h)
A = 2pi*4.5(4.5 + 9)
A = 121.5pi
Hemisphere:
surface area of hemisphere = (area of circular base)+(half of surface area of sphere)
B = (pi*r^2) + (0.5*(4pi*r^2))
B = pi*r^2 + 2pi*r^2
B = 3pi*r^2
B = 3pi*(4.5)^2
B = 60.75pi
A+B = 121.5pi + 60.75pi
A+B = 182.25pi
It appears choice (b) is the final answer.
But be careful: this is trick/trap your teacher set up.
The calculation A+B counts the circular base of the hemisphere and the circular top of the cylinder.
These two circles are NOT part of the external surface area.
They are covered up when the shapes combine.
Think of them as internal walls that are not part of the exterior of the house.
We'll subtract off two copies of pi*r^2 = pi*(4.5)^2 = 20.25pi
So we subtract 2*20.25pi = 40.5pi square cm of area.
182.25pi - 40.5pi = 141.75pi
Answer: a) 141.75pi
Question 1199755: Two identical spheres of diameter 6 cm have the same total volume as
a) one sphere with diameter 12 cm
b) four identical spheres each with diameter 3 cm
c) eight identical spheres each with diameter 4 cm
d) sixteen identical spheres each with diameter 3 cm
e) thirty-two identical spheres each with diameter 2 cm
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The volume is proportional to the cube of the diameter. So for the total volume to stay the same, you can...
(1) double (multiply by 2) the diameter and divide the number of spheres by 2^3=8
(2) divide the diameter by 2 and multiply the number of spheres by 2^3=8
or, in general,
(3) divide the diameter by a factor x and multiply the number of spheres by x^3
Option (2) above gives you a diameter of 6/2 = 3 cm and 2(2^3) = 2(8) = 16 spheres, which is answer choice d.
ANSWER: d) 16 spheres each with diameter 3cm
Question 1199293: A cylinder has a volume of 484π in.3 and a height of 4 in.
What is the radius of the cylinder?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Divide the volume by the height to find the area of the circular base.
Knowing the area of the circular base, find the radius of the base.
Happy calculations !
Question 1198554: The area of a base of a cone is two-thirds the area of a base of a cylinder and their volumes are equal. Find the ratio of their altitudes.
Found 2 solutions by math_tutor2020, Shin123:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
VL = volume of cylinder
VC = volume of cone
VC = VL since we're told these particular cone and cylinder have equal volume.
HL = height of the cylinder
HC = height of the cone
AL = area of the cylinder circular base
AC = area of the cone circular base
AC = (2/3)*AL
VL = (area of base)*(height)
VL = (AL)*(HL)
VC = (1/3)*(area of base)*(height)
VC = (1/3)*(AC)*(HC)
VC = (1/3)*((2/3)*AL)*(HC)
VL = (2/9)*AL*HC
(AL)*(HL) = (2/9)*AL*HC
HL = (2/9)*HC
HL/HC = 2/9
HC/HL = 9/2
The ratio of the cone's height (HC) over the cylinder's height (HL) is 9/2.
Answer by Shin123(626)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the radius of the cone be  , the radius of the cylinder be , the radius of the cylinder be  , the height of the cone , the height of the cone  , and the height of the cylinder , and the height of the cylinder  . Then, we have the equation . Then, we have the equation  . Our goal is to find . Our goal is to find 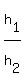 . First, we can divide . First, we can divide  from both sides to get from both sides to get  . We can multiply both sides by 3, then divide both sides by . We can multiply both sides by 3, then divide both sides by 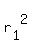 to get to get  . Dividing both sides by . Dividing both sides by  , we get , we get 
Since we know that the base of the cone is two-thirds the area of the base of the cylinder, we have the equation  . Dividing both sides by . Dividing both sides by  , we get , we get  . Multiplying both sides by . Multiplying both sides by  , we get , we get  . Finally, dividing both sides by . Finally, dividing both sides by 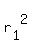 gives us gives us  . We can plug this into the first equation to get . We can plug this into the first equation to get  . .
The question doesn't state whether you want the ratio of the height of the cone over the height of the cylinder (which was what I derived), or the ratio of the height of the cylinder over the height of the cone. If you want that, the answer would instead be  . .
Question 1198560: A plane is passed through a right circular cone parallel to the base and 0.6 m from the vertex. The altitude and basal diameter of the cone are 1.5 m and 1.2 m, respectively. Find the volume of the frustum of this cone.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1198550: The base of a conical vessel is 1,000 cm^2. How many liters of water can it contain if it is 1 meter deep?
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1198552: A circular conical container with a radius of 3 inches and an altitude of 4 inches. How many can it hold in π cubic inches of water?
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1198022: A closed cylindrical tank is 8 feet long and 3feet in
diameter. When lying in a horizontal position, the water
is 2 feet deep. If the tank is in the vertical position, the
depth of water in the tank is?
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The height relative to the 8ft length will be in the same proportion as the area of the 'filled' portion of the cross-sectional (circle) area while horizontal.
The part that is filled is a segment of the circle, plus two right triangles that fill in the 'wedge'

So the height when the cylinder is vertical is:

Sorry for the scattered format, all the information is there... There may be more optimal ways to compute the answer.
Question 1197968: A ball is thrown with initial speed of 25 miles per hour in a direction that makes an angle of 30 degrees with the horizontal. What are the components of the velocity?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
At the angle to the horizontal of 30 degrees, vertical component of the speed is
sin(30°) = 0.5 of the magnitude of the initial speed
and horizontal component is cos(30°) =  = 0.866 of the magnitude of the initial speed. = 0.866 of the magnitude of the initial speed.
Question 1197969: A child is spinning a rock at the end of a 2 foot rope at the rate of 180 revolutions per minute (rpm). What is the linear speed of the rock on feet per minute?
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1195855: Calculate for the surface area of a frustum of a sphere if the diameter of its ends are 80 cm and 120 cm and the thickness is 30 cm.
Answer by MathLover1(20849)   (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990
|
| |