Question 1177261: According to Masterfoods, the company that manufactures M&M’s, 12% of peanut M&M’s are brown, 15% are yellow, 12% are red, 23% are blue, 23% are orange and 15% are green. You randomly select five peanut M&M’s from an extra-large bag of the candies. (Round all probabilities below to four decimal places; i.e. your answer should look like 0.1234, not 0.1234444 or 12.34%.)
Compute the probability that exactly two of the five M&M’s are orange.
Incorrect I set it up as 23C2 77C3
---------
100C5
Is it set up correctly?
Compute the probability that two or three of the five M&M’s are orange.
Compute the probability that at most two of the five M&M’s are orange.
Compute the probability that at least two of the five M&M’s are orange. $36.4714$Incorrect
If you repeatedly select random samples of five peanut M&M’s, on average how many do you expect to be orange? (Round your answer to two decimal places.)
orange M&M’s
With what standard deviation? (Round your answer to two decimal places.)
orange M&M’s
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
According to Masterfoods, the company that manufactures M&M’s, 12% of peanut M&M’s are brown,
15% are yellow, 12% are red, 23% are blue, 23% are orange and 15% are green.
You randomly select five peanut M&M’s from an extra-large bag of the candies.
(Round all probabilities below to four decimal places; i.e. your answer should look like 0.1234, not 0.1234444 or 12.34%.)
(a) Compute the probability that exactly two of the five M&M’s are orange.
(b) Compute the probability that two or three of the five M&M’s are orange.
(c) Compute the probability that at most two of the five M&M’s are orange.
(d) Compute the probability that at least two of the five M&M’s are orange.
If you repeatedly select random samples of five peanut M&M’s, on average how many do you expect to be orange? (Round your answer to two decimal places.)
orange M&M’s
With what standard deviation? (Round your answer to two decimal places.)
orange M&M’s
~~~~~~~~~~~~~~~~~
I will not answer all the questions - I will answer only questions (a), (b), (c) and (d).
(a) Compute the probability that exactly two of the five M&M’s are orange
P(2 of 5 are red) = = 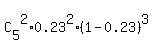 =  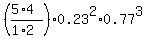= 0.2415 (rounded) ANSWER
(b) Compute the probability that two or three of the five M&M’s are orange
P(2 or 3 of 5 are red) = P(2 of 5 are red) + P(3 of 5 are red) =
= + 
I leave it to you to complete the calculations having the formula ready to use in front of you.
(c) Compute the probability that at most two of the five M&M’s are orange.
P(at most 2 of 5 are red) = P(0 of 5 are red) + P(1 of 5 are red) + P(2 of 5 are red) =
=  +  +
I leave it to you to complete the calculations having the formula ready to use in front of you.
(d) Compute the probability that at least two of the five M&M’s are orange.
P(at least 2 of 5 are red) = P(2 of 5 are red) + P(3 of 5 are red) + P(4 of 5 are red) + P(5 of 5 are red)
= + +  +  .
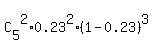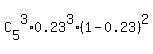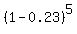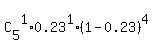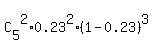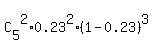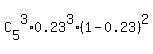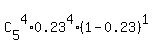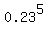I leave it to you to complete the calculations having the formula ready to use in front of you.
All these questions (a) - (d) are about the BINOMIAL DOSTRIBUTION probability with the number of trials equal to 5
and the probability of the successful trial of 0.23.
The number of successful trials is different in different parts from (a) to (d).
To see many other similar and different solved problems of this kind, look into the lessons
- Simple and simplest probability problems on Binomial distribution
- Typical binomial distribution probability problems
- How to calculate Binomial probabilities with Technology (using MS Excel)
- Solving problems on Binomial distribution with Technology (using MS Excel)
- Solving problems on Binomial distribution with Technology (using online solver)
in this site.
You will find there many similar typical problems of this class, solved and explained with all details.
After reading these lessons, you will be able to solve such problems on your own, which is your
PRIMARY MAJOR GOAL visiting this forum (I believe).
|
|
|
