Tutors Answer Your Questions about Binomial-probability (FREE)
Question 1166928: the weight of a small starbucks coffee is a normally distributed random variable with a mean of 325 grams and a standard deviation of 10 grams. find the weight that corresponds to each event?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
the weight of a small starbucks coffee is a normally distributed random variable with a mean of 325 grams
and a standard deviation of 10 grams. find the weight that corresponds to each event?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Corresponds to WHAT event ?
From your post, I clearly see that you even do not read what you post.
Question 1167860: The physical plant at the main campus of a large state university recieves daily requests to replace florecent lightbulbs. The distribution of the number of daily requests is bell-shaped and has a mean of 49 and a standard deviation of 5. Using the 68-95-99.7 rule, what is the approximate percentage of lightbulb replacement requests numbering between 44 and 49?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The physical plant at the main campus of a large state university receives daily requests
to replace florescent lightbulbs. The distribution of the number of daily requests is bell-shaped
and has a mean of 49 and a standard deviation of 5. Using the 68-95-99.7 rule,
what is the approximate percentage of lightbulb replacement requests numbering between 44 and 49?
~~~~~~~~~~~~~~~~~~~~~~~
Notice that in this problem, 44 is 5 units, or exactly one standard deviation, below
the mean of 49.
Therefore, the approximate percentage of lightbulb replacement requests numbering between
44 and 49 is
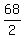 = 34%. ANSWER = 34%. ANSWER
Solved.
Question 1209744: Dandelions are studied for their effects on crop production and lawn growth. In one region, the mean number of dandelions per square meter was found to be 9.9.
Find the probability of no dandelions in an area of 1 m².
Find the probability of at least one dandelion in an area of 1 m².
P(at least one) =
0.99995
Correct
Find the probability of at most two dandelions in an area of 1 m².
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! You're on the right track using the Poisson distribution! Here's how to calculate the probabilities:
**1. Probability of no dandelions:**
* The Poisson distribution formula is: P(x) = (e^-μ * μ^x) / x!
* Where:
* P(x) is the probability of x events occurring
* e is the base of the natural logarithm (~2.71828)
* μ is the mean number of events (9.9 dandelions per square meter)
* x is the number of events we're interested in (0 dandelions)
* x! is the factorial of x (0! = 1)
* Plugging in the values: P(0) = (e^-9.9 * 9.9^0) / 1
* Calculating this gives you approximately 0.0000504
**2. Probability of at least one dandelion:**
* This is the complement of having no dandelions. So:
* P(at least one) = 1 - P(0)
* P(at least one) = 1 - 0.0000504
* P(at least one) ≈ 0.9999496 (which rounds to 0.99995 as you correctly stated)
**3. Probability of at most two dandelions:**
* This means we want the probability of having 0, 1, or 2 dandelions. We need to calculate each of these probabilities and add them together:
* P(0) = 0.0000504 (calculated above)
* P(1) = (e^-9.9 * 9.9^1) / 1! ≈ 0.0004988
* P(2) = (e^-9.9 * 9.9^2) / 2! ≈ 0.002469
* P(at most two) = P(0) + P(1) + P(2)
* P(at most two) ≈ 0.0000504 + 0.0004988 + 0.002469
* P(at most two) ≈ 0.0030182
**Therefore, the probability of at most two dandelions in an area of 1 m² is approximately 0.0030182**
Question 1186719: A “fair,” “relatively thick” coin, when flipped, can show heads (H) or tails (T) with equal probabilities, but it is also probable to come to rest on its edge (E) with a probability of 4.5% (0.045). Showing your work, answer the following questions
1. Set up a probability distribution table for the three possible events.
2. If the coin were flipped twice, what would be the probability that it would show tails the first time and would come to rest on its edge the second time? Provide a brief explanation to support your computation(s). Show the probability value in 4 decimal places.
3. If the coin were flipped 14 times, what would be the probability that the coin would come to rest on its edge (“getting edge”) at most twice? Showing your work, report the probability value in 4 decimal places. Treat the problem as a binomial experiment.
4. Determine the probability of getting heads between 4 to 6 times (both inclusive), i.e., 4 times, 5 times, or 6 times, when the coin is flipped 14 times. Showing your work, report the probability value in 4 decimal places. Treat the problem as a binomial experiment.
5. What is the probability of getting “heads or tails” at least once when the coin is flipped 14 times? Showing your work, report the probability value in 4 decimal places. Treat the problem as a binomial experiment.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's the solution:
**1. Probability Distribution Table:**
| Outcome | Probability |
|---|---|
| Heads (H) | 0.4775 |
| Tails (T) | 0.4775 |
| Edge (E) | 0.045 |
*Explanation:* The probabilities of heads and tails must be equal since the coin is fair. Since the total probability must equal 1, we have: P(H) + P(T) + P(E) = 1. Therefore, 2P(H) + 0.045 = 1, so P(H) = P(T) = (1 - 0.045) / 2 = 0.4775.
**2. Probability of Tails then Edge:**
The flips are independent events. Therefore, we multiply the probabilities:
P(T then E) = P(T) * P(E) = 0.4775 * 0.045 = 0.0214875 ≈ 0.0215
**3. Probability of at most two edges in 14 flips:**
This is a binomial probability problem. Let X be the number of times the coin lands on its edge. We want to find P(X ≤ 2). The probability of "success" (landing on edge) is p = 0.045, and the number of trials is n = 14.
P(X ≤ 2) = P(X=0) + P(X=1) + P(X=2)
The binomial probability formula is: P(X=k) = (nCk) * p^k * (1-p)^(n-k), where nCk is "n choose k".
* P(X=0) = (14C0) * (0.045)^0 * (0.955)^14 ≈ 0.5204
* P(X=1) = (14C1) * (0.045)^1 * (0.955)^13 ≈ 0.3587
* P(X=2) = (14C2) * (0.045)^2 * (0.955)^12 ≈ 0.1090
P(X ≤ 2) ≈ 0.5204 + 0.3587 + 0.1090 ≈ 0.9881
**4. Probability of 4 to 6 heads in 14 flips:**
This is also a binomial probability problem. The probability of "success" (getting heads) is p = 0.4775, and n = 14. We want to find P(4 ≤ X ≤ 6) = P(X=4) + P(X=5) + P(X=6).
* P(X=4) = (14C4) * (0.4775)^4 * (0.5225)^10 ≈ 0.1920
* P(X=5) = (14C5) * (0.4775)^5 * (0.5225)^9 ≈ 0.2253
* P(X=6) = (14C6) * (0.4775)^6 * (0.5225)^8 ≈ 0.1966
P(4 ≤ X ≤ 6) ≈ 0.1920 + 0.2253 + 0.1966 ≈ 0.6139
**5. Probability of at least one "heads or tails" in 14 flips:**
Since the only other outcome is "edge," getting "heads or tails" is the complement of getting "edge" on all 14 flips.
P(at least one H or T) = 1 - P(all edges)
P(all edges) = (0.045)^14 ≈ 2.91 x 10⁻¹⁸
P(at least one H or T) = 1 - (0.045)^14 ≈ 1.0000
Question 1195769: 1. As part of a study to determine the effect of bumetanide on urinary calcium excretion, nine randomly selected men each received an oral dose of .5 mg of the drug. Urine was collected hourly for the next six hours. The mean excretion rate for this sample of nine men was found to be 7.5 mg/hr, with a standard deviation of 6.0 mg/hr.
a. What is the 98% confidence interval estimate of the population mean excretion rate for all men receiving bumetanide? Interpret this interval.
b. Urine was also collected from a random sample of 16 men who did not receive bumetanide. The mean excretion rate for this sample was 6.5 mg/hr, with a standard deviation of 2.0 mg/hr. What is the 98% confidence interval estimate of the difference in excretion rates between the population of men receiving the drug and the population of men who did not receive it?
Answer by proyaop(69)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, let's calculate the confidence intervals.
**a. 98% Confidence Interval for the Population Mean Excretion Rate (Bumetanide Group)**
* **Given:**
* Sample size (n1) = 9
* Sample mean (x̄1) = 7.5 mg/hr
* Sample standard deviation (s1) = 6.0 mg/hr
* Confidence level = 98%
* **Find:**
* Critical value (tα/2)
* Margin of error (E)
* Confidence interval
1. **Find the critical value (tα/2)**:
* Degrees of freedom (df) = n1 - 1 = 9 - 1 = 8
* α = 1 - 0.98 = 0.02
* α/2 = 0.01
Using a t-distribution table or a calculator, find the t-value for df = 8 and α/2 = 0.01.
* tα/2 ≈ 2.896
2. **Calculate the standard error:**
* Standard error (SE) = s1 / √n1 = 6.0 / √9 = 2.0 mg/hr
3. **Calculate the margin of error (E):**
* E = tα/2 * SE = 2.896 * 2.0 = 5.792 mg/hr
4. **Calculate the confidence interval:**
* Lower limit = x̄1 - E = 7.5 - 5.792 = 1.708 mg/hr
* Upper limit = x̄1 + E = 7.5 + 5.792 = 13.292 mg/hr
* **Interpretation:**
We are 98% confident that the true population mean urinary calcium excretion rate for all men receiving bumetanide lies between 1.708 mg/hr and 13.292 mg/hr.
**b. 98% Confidence Interval for the Difference in Excretion Rates**
* **Given:**
* Sample size for bumetanide group (n1) = 9
* Sample mean for bumetanide group (x̄1) = 7.5 mg/hr
* Sample standard deviation for bumetanide group (s1) = 6.0 mg/hr
* Sample size for no bumetanide group (n2) = 16
* Sample mean for no bumetanide group (x̄2) = 6.5 mg/hr
* Sample standard deviation for no bumetanide group (s2) = 2.0 mg/hr
* Confidence level = 98%
* **Find:**
* Degrees of freedom (df)
* Pooled standard deviation (sp)
* Standard error of the difference (SEdiff)
* Critical value (tα/2)
* Margin of error (E)
* Confidence interval
1. **Calculate degrees of freedom (df):**
* Using the Welch-Satterthwaite equation for unequal variances:
df ≈ [(s1^2/n1 + s2^2/n2)^2] / [(s1^2/n1)^2/(n1-1) + (s2^2/n2)^2/(n2-1)]
df ≈ [(6.0^2/9 + 2.0^2/16)^2] / [(6.0^2/9)^2/(9-1) + (2.0^2/16)^2/(16-1)]
df ≈ 14.17
(Round down to 14 for t-distribution table lookup)
2. **Calculate the pooled standard deviation (sp):**
* Since we are assuming unequal variances, we do not calculate a pooled standard deviation.
3. **Calculate the standard error of the difference (SEdiff):**
* SEdiff = √[(s1^2/n1) + (s2^2/n2)]
* SEdiff = √[(6.0^2/9) + (2.0^2/16)]
* SEdiff = √(4 + 0.25) = √4.25 ≈ 2.06 mg/hr
4. **Find the critical value (tα/2):**
* α = 1 - 0.98 = 0.02
* α/2 = 0.01
* Using a t-distribution table with df = 14, find tα/2 for α/2 = 0.01.
* tα/2 ≈ 2.624
5. **Calculate the margin of error (E):**
* E = tα/2 * SEdiff = 2.624 * 2.06 = 5.40 mg/hr
6. **Calculate the confidence interval:**
* Lower limit = (x̄1 - x̄2) - E = (7.5 - 6.5) - 5.40 = -4.40 mg/hr
* Upper limit = (x̄1 - x̄2) + E = (7.5 - 6.5) + 5.40 = 6.40 mg/hr
* **Interpretation:**
We are 98% confident that the true difference in mean urinary calcium excretion rates between the population of men receiving bumetanide and the population of men who did not receive it lies between -4.40 mg/hr and 6.40 mg/hr.
**Note:**
* The confidence intervals are based on the assumption of normality within each group.
* The Welch-Satterthwaite equation is used to approximate the degrees of freedom when the population variances are assumed to be unequal.
I hope this helps! Let me know if you have any further questions.
Question 1208472: The chance that a U.S. police chief believes the death penalty “significantly reduces the number of homicides” is 1 in 4. If a random sample of 8 police chiefs is selected, find the probability that at most 3 believe that the death penalty significantly reduces the number of homicides.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 0.88618 (approximate)
--------------------------------------------------------------------------
Quick way to find the answer using technology
On a TI83 or similar, you would use the BinomCDF command.
The order of inputs is: n, p, kn = number of trials = 8
p = probability of success = 0.25
k = number of successes = 3 Type in BinomCDF(8,0.25,3) to get the approximate result 0.88618
The answer will vary depending how you round it.
Here are some alternative technology options.- Search out "binomial CDF calculator". This page and this page are two of many results. Feel free to explore your favorite.
- Use the Probability Calculator in GeoGebra. Select "binomial" from the dropdown menu. Type n = 8 and p = 0.25; the goal is to calculate
) - Use the spreadsheet command called BinomDist. The input would be =BinomDist(3,8,0.25,true)
- Use the BinomialDist command in GeoGebra. Note "binomial" instead of "binom". The input would be BinomialDist(8,0.25,3,true)
Refer to the help manual for more information.
--------------------------------------------------------------------------
The slightly longer method
The binomial probability formula is
B(x) = (nCx)*(p^x)*(1-p)^(n-x)
where,n = number of trials
p = probability of success
x = number of successes The nCx refers to the nCr combination formula. These values are found in Pascal's Triangle. A quick way to calculate the nCr values is to use the Combin function in a spreadsheet. Or you can use a TI Calculator.
Like with many things in math, there are many options to calculate nCr.
Let's calculate the probability of exactly 0 police chiefs believe that the death penalty significantly reduces the number of homicides.
B(x) = (nCx)*(p^x)*(1-p)^(n-x)
B(x) = (8Cx)*(0.25^x)*(1-0.25)^(8-x)
B(0) = (8C0)*(0.25^0)*(1-0.25)^(8-0)
B(0) = (1)*(0.25^0)*(1-0.25)^(8-0)
B(0) = 0.10011292
This value is approximate.
It is possible to calculate by hand, given a very long time, but I recommend a calculator.
Repeat the process to find these other values
B(1) = 0.26696777
B(2) = 0.3114624
B(3) = 0.2076416
I'll skip showing the steps for these.
Therefore,
B(0)+B(1)+B(2)+B(3)
= 0.10011292+0.26696777+0.3114624+0.2076416
= 0.88618469
= 0.88618
The answer will vary depending how you round it.
More practice with the Binomial Distribution is found on this page
Question 1208174: Mr. Taylor filled out a bracket for the NCAA national tournament based on his knowledge of college basketball. He has a 0.46. Probability of guessing anyone game correctly what is the probability Mr. Taylor will pick all 32 of the first round games correctly what is the probability Mr. Taylor will pick exactly 18 games correctly in the first round what is the probability Mr. Taylor will pick at least 18 games correctly in the first round what is the probability Mr. Taylor will pick exactly 22 games incorrectly in the first round.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Jeepers! Didn't you learn that you must put a punctuation mark at the end of
a sentence, and to begin the next sentence with a capital letter? You are
to put a period, (you know, a dot like this " . "), at the end of a declarative
sentence, and a question mark, (a hook like this " ? ") at the end of an
interrogative sentence.
This is the correct way to write your problem:
Mr. Taylor filled out a bracket for the NCAA national tournament based on his
knowledge of college basketball.
He has a 0.46 probability of guessing any one game correctly.
What is the probability that Mr. Taylor will pick:
(a) all 32 of the first round games correctly?
(b) exactly 18 games correctly in the first round?
(c) at least 18 games correctly in the first round?
(d) exactly 22 games incorrectly in the first round.
Now if you'll post the problem like that, maybe one of us will answer. Try it
and see.
Edwin
Question 1208046: A fair die is thrown once. Find the probability of obtaining :a six, an even number, a number greater than 3,a three or a five
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor interpreted this as four different cases. It can also be interpreted as a single case.
"...a six, (or) an even number, (or) a number greater than 3, (or) a three or a five"
a six: only one number, 6
an even number: 2, 4 or 6
a number greater than 3: 4, 5, or 6
a three or a five: 3 or 5
All together: 2, 3, 4, 5, or 6
ANSWER: 5/6
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A fair die is thrown once. Find the probability of obtaining:
(a) a six,
(b) an even number,
(c) a number greater than 3,
(d) a three or a five
~~~~~~~~~~~~~~~~~~
(a) P(a six) = P(a six of 6) = 1/6.
(b) P(an even number) = P(2 or 4 or 6 of 6) = 3/6 = 1/2.
(c) P(a number greater than 3) = P(4 or 5 or 6 of six) = 3/6 = 1/2.
(d) P(a three or a five) = P(3 or 5 of 6) = 2/6 = 1/3.
Solved.
Question 1207193: A special deck of 16 cards has 4 that are blue, 4 yellow, 4 green, and 4 red. The four
cards of each color are numbered 1 through 4. A single card is drawn at random. Define
events
B: the card is blue
R: the card is red
N: the number on the card is at most two
(a) List the outcomes that comprise B, R, and N. (Use notation like B3 to represent a
blue card with a 3 on it.)
(b) List the outcomes that comprise B ∩ R, B ∪ R, B ∩ N, R ∪ N, B, and B ∪ R.
(c) Assuming all outcomes are equally likely, find the probabilities of the events in the
previous part.
(d) Determine whether or not B and N are mutually exclusive. Explain why or why not.
3. (O7) In early 2001, the United States Census Bureau started releasing the results of th
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The deck = {B1,B2,B3,B4,Y1,Y2,Y3,Y4,G1,G2,G3,G4,R1,R2,R3,R4}
------------------------------------------------------------------
(a)
I'll do B and R in the (a) part for you:
B = {B1,B2,B3,B4}
R = {R1,R2,R3,R4}
You do the N part. Here's how:
N = ?. If the number on the card is at most two, then that number is either 2,3,
or 4. So look through the deck and list all the cards that have a 2,3, or 4 on
them regardless of what letter it has before the number. List them all between
braces {} with commas separating them.
------------------------------------------------------------------
(b)
B ∩ R = ?. Are there any blue cards that are also red cards? If so list
them between braces {} with commas separating them. If not, write the empty set
∅ or { },
B ∪ R = ?. List all the cards that are either in B and/or in R between braces
{}, with commas separating them.
B ∩ N = ?. Are there any cards that are both in B and N? If so, list them
between braces {} with commas separating them. If not, write the empty set
∅ or { },
R ∪ N = ?. List all the cards that are either in R and/or in N between braces
{}, with commas separating them.
B = ?. Just copy what I gave you above for B.
B ∪ R = ?. List all the cards that are either in B and/or in R between braces
{}, with commas separating them.
------------------------------------------------------------------
(c) In each of these, count the number of cards in the set which the probability
is asked for. Write this as the numerator of a fraction. Then count the number
of cards in the deck, and write this as the denominator of the fraction. Reduce
the fraction if possible. This will be the answer in each case.
------------------------------------------------------------------
(d) Sets are said to be "mutually exclusive" when they have NO elements in
common. [The word "exclusive" is not to be taken as what "exclusive" usually
means. When you see the words "mutually exclusive", think of the word
"exclusive" and though it were the word "excluding" instead. It means that each
of the two sets 'excludes' all (does not contain any) of the members or elements
of the other set.]
So use that to answer (d).
------------------------------------------------------------------
(3) Looks like you copied and pasted too much. LOL
Edwin
Question 1204476: . Airlines sell more tickets for a flight than the number of available seats (overbooking). They do this because they know from past experience that only 90% of ticketed passengers actually show up for the flight.
(a) A plane has 9 seats. If the airline sells 11 tickets for a flight, what is the probability that the flight will be overbooked (the number of passengers who show up is greater than the number of available seats)?
(b) A plane has 235 seats. If the airline sells 250 tickets for a flight, what is the probability that the flight will be overbooked (the number of passengers who show up is greater than the number of available seats)? Use the normal approximation for this please
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1204338: An exam consists of 20 multiple choice questions, each with 5 answer choices. If a student guesses on every question, this a binomial experiment with the random variable
X
=
Number of questions answered correctly
What is the probability that the student answers exactly 4 questions correctly?
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1203585: The time required to complete a college achievement test was foundto be normally
distributed, with a mean of 110 minutes and standard deviation of20 minutes.
(a) What proportion of the students will ?nish within 2 hours (120minutes)?
(b) What proportion of the students will ?nish at exactly 2hours?
(c) When should the test be terminated to allow just enough timefor 90% of the
students to complete the test
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! mean is 110 minutes.
standard deviation is 20 minutes.
use the z-score formula.
it is z = (x - m) / s
z is the z-score
m is the population mean
s is the standard deviation
x is the student score
The time required to complete a college achievement test was found to be normally distributed, with a mean of 110 minutes and standard deviation of20 minutes.
(a) What proportion of the students will finish within 2 hours (120 minutes)?
z = (120 - 110) / 20 = .5
area to the left of a z-score of .5 = .6915.
this means that 69.15% of the participants will complete the test in 120 minutes or less.
(b) What proportion of the students will finish at exactly 2 hours?
the theory says that, because this is a continuous curve, the probability of getting exactly 120 minutes is 0.
here's refference that addresses that issue.
https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_probability/bs704_probability8.html#:~:text=Note%20that%20with%20the%20normal,is%20%3C%2029%20is%2050%25.
the particular statement in that reference is:
Note that with the normal distribution the probability of having any exact value is 0 because there is no area at an exact BMI value, so in this case, the probability that his BMI = 29 is 0, but the probability that his BMI is <29 or the probability that his BMI is < 29 is 50%.
(c) When should the test be terminated to allow just enough time for 90% of the
students to complete the test.
z-score that has 90% of the area under the normal distribution curve to the left of it is equal to 1.2816.
z-score formula becomes:
1.2816 = (x - 110) / 20
solve for x to get x = 20 * 1.2816 + 110 = 135.632.
that's the number of minutes that the test would be terminated so that 90% of the participants will have been able to complete the test.
any rounding should be rounding up to ensure at least 90%.
Question 1202956: A committee consisting of 3 men and 4 women is to be choose at random from 5 women and 6 men. What is the probability that one particular women and man will be on it.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
"Choose" the one particular man and one particular woman and put them on the committee.
There are 4 women and 5 men left, from which you need to choose 2 men and 3 women: C(4,3)*C(5,2) = 4*10 = 40
The total number of ways of choosing the last 5 members of the committee out of the remaining 9 people without restrictions is C(9,5) = 126
ANSWER: 40/126 = 20/63
----------------------------------------------------------------
Revised answer after seeing the response from tutor @ikleyn....
The above solution only makes sure that one particular man and one particular woman have to be on the committee; it overlooks the fact that the committee must contain 3 men and 4 women.
Total number of ways of choosing 3 of the 6 men and 4 of the 5 women is
C(6,3)*C(5,4) = 20*5 = 100
So the answer to the question is 40/100 = 2/5 = 40% = 0.4
Question 1202716: You are taking a true/false test that has 60 questions If you guess on each question, and have the same chance of guessing the correct answer on each question, what is the probability you get at least 65% of the questions correct?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You are taking a true/false test that has 60 questions.
If you guess on each question, and have the same chance of guessing the correct answer
on each question, what is the probability you get at least 65% of the questions correct?
~~~~~~~~~~~~~~~~~~~
The original problem is a binomial distribution probability problem.
The number of trials is n= 60; the probability of success is p= 1/2 = 0.5
for each individual trial.
Since the number of trials is great, the method of solution is to use a normal
distribution approximation.
About approximation of the binomial distribution by normal distribution and continuity correction factor
see your textbook and/or these Internet sources
https://www.statology.org/normal-approximation
https://www.statisticshowto.com/probability-and-statistics/binomial-theorem/normal-approximation-to-the-binomial/
https://online.stat.psu.edu/stat414/lesson/28/28.1
https://stats.libretexts.org/Courses/Las_Positas_College/Math_40%3A_Statistics_and_Probability/06%3A_Continuous_Random_Variables_and_the_Normal_Distribution/6.04%3A_Normal_Approximation_to_the_Binomial_Distribution
For this normal distribution approximation, the mean value is m = n*p = 0.5*60 = 30;
the standard deviation is 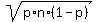 = = 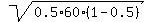 = 3.87298 (rounded).
Next, at least 65% of 60 questions is at least = 3.87298 (rounded).
Next, at least 65% of 60 questions is at least  = 39 questions to answer correctly.
Therefore, to answer the problem's question, you should find the area under the the described
normal curve on the RIGHT of the raw mark 38.5 (we use the continuity correction factor).
So, if you use a regular calculator TI-83 or TI-84, you can get the answer using
the standard normalcdf function
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(38.5, -9999, 30, 3.87298).
You get the value of 0.014 (rounded). ANSWER = 39 questions to answer correctly.
Therefore, to answer the problem's question, you should find the area under the the described
normal curve on the RIGHT of the raw mark 38.5 (we use the continuity correction factor).
So, if you use a regular calculator TI-83 or TI-84, you can get the answer using
the standard normalcdf function
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(38.5, -9999, 30, 3.87298).
You get the value of 0.014 (rounded). ANSWER
Solved.
--------------------
If you are a beginner student in learning normal probability distribution, I advise you
to start learning this kind of computations using the online free of charge calculator
https://onlinestatbook.com/2/calculators/normal_dist.html
It provides a graphical support, so at each step you do understand what you are doing.
In addition, this graphical support prevents you from making mistakes.
When you learn enough this kind of computations, you can switch to your regular calculator,
but even then you may use the online calculator for checking purposes.
/////////////////////
Let's check the answer using direct computations for the binomial distribution.
In this case, we should find the probability P = P(n=60; k >= 39; p= 0.5)
The easiest way to compute it is to use the online free of charge calculator
https://stattrek.com/online-calculator/binomial
It gives the answer 0.014 (rounded).
Question 1202116: A grocery store counts the number of customers who arrive during an hour. The average over a year is 19 customers per hour. Assume the arrival of customers follows a Poisson distribution. (It usually does.)
Find the probability that at least one customer arrives in a particular one minute period. Round your answer to 3 decimals.
Find the probability that at least two customers arrive in a particular 5 minute period. Round your answer to four decimals.
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! 19 per hour is 19/12 per 5 minute period, since it is proportional to time.
it is 19/60 per 1 minute period.
probability that at least 1 customer arrives in a 1 minute period is 1-P(0) arrive in that time.
P(0)=e^-19/60=0.7286, so the answer is 1-0.729=0.271.
--
at least 2 means 1-P(0)-P(1)
P(0)=e^-19/12=0.2053
P(1)=e-19/12*19/12^1/1!=0.3250
so at least two customers would be 1-P(0)-P(1)=1-0.2053-0.3250=0.4697
Question 1199983: A jar contains a very large number of purple jelly beans and green jelly beans. There are three times as many purple ones as green ones. If an individual chooses 5 beans from the jar, estimate the probability that 3 of the beans will be green?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A jar contains a very large number of purple jelly beans and green jelly beans.
There are three times as many purple ones as green ones.
If an individual chooses 5 beans from the jar, estimate the probability
that 3 of the beans will be green?
~~~~~~~~~~~~~~~~~
It is a binomial distribution probability problem.
p = P(success) = P(green) = 1/4 = 0.25; q = 1-p = P(purple) = 3/4 = 0.75.
number of trials n= 5;
number of successful trials k= 3 (3 green beans of 5).
The probability under the question is
P(n=5; k=3; p=0.25) = 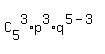 = =  = 0.0879 (rounded). ANSWER = 0.0879 (rounded). ANSWER
Solved.
----------------
To see many other similar (and different) solved problems, look into the lessons
- Simple and simplest probability problems on Binomial distribution
- Typical binomial distribution probability problems
in this site.
Question 1199468: (x:100,0.3)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One hundred years ago, there were old movies without words, and everything was clear there.
Your post is also without words, but in contrast with those movies, nothing is clear in it . . .
May I ask - what do you want from us, the tutors ?
Question 1198390: Among 200 patients at a Tikur Anbessa hospital. 40 of them are
cardiac patients, 100 of them are cancer, patients and 60 of
them are diabetic patients. The hospital wants to give free
medical service for some patients. ♦ A) What is the probability that 5 cardiac and 10 cancer patients
are given free medical treatment? ♦ B) What is the probability that 2 cardiac and 5 cancer patients and 4 diabetic patients are given free medical treatment?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As it is worded, printed and presented in the post, the problem is posed incorrectly.
To be correct, the problem must say in the description,
that the number of free services that they want to provide is 15 in case (A) and 11 in case (B).
Without it, the problem can not be solved properly and is nonsense.
It is not for the first time this problem comes to the forum in this form,
and I just reacted on it in similar way earlier.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In case A, 15 of the 200 patients are chosen; and they are 5 of the 40 cardiac patients and 10 of the 100 cancer patients. The probability is
(40 choose 5)*(100 choose 10)
-------------------------------
200 choose 15
Use a calculator and express the result in the desired/required form.
Case B is similar; the probability is
(40 choose 2)*(100 choose 5)*(60 choose 4)
--------------------------------------------
200 choose 11
Question 1198389: Among 200 patients at a Tikur Anbessa hospital. 40 of them are
cardiac patients, 100 of them are cancer, patients and 60 of
them are diabetic patients. The hospital wants to give free
medical service for some patients. ♦ A) What is the probability that 5 cardiac and 10 cancer patients
are given free medical treatment
Found 2 solutions by ikleyn, ewatrrr:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As it is worded, printed and presented in the post, the problem is posed incorrectly.
To be correct, the problem must say in the description,
that the number of free services that they want to provide is 15.
Without it, the problem can not be solved properly.
It is not for the first time this problem comes to the forum in this form,
and I just reacted on it in similar way earlier.
Answer by ewatrrr(24785)   (Show Source): (Show Source):
Question 1195775: find the indicated probabilities. about 30% of U.S. adults are trying to lose weight. you randomly select eight U.S. adults. find the probability that the number of U.S. adults who say they are trying to lose weight is (a) exactly three, (b) at least three, and (c) more than three
Found 2 solutions by ikleyn, Boreal:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is binomial because n is fixed, assume constant probability and independence of random samples.
a. 8C3*0.3^3*0.7^5=0.2541
b. look at 0,1,2
for 0 it is 0.7^8=0.0576
for 1 it I 8*0.3*0.7^7=0.1977
for 2 it is 28*0.3^2*0.7^6=0.2965
The sum of those is 0.5088
so at least 3 is everything else or 1-0.5088 or 0.4912 .
c. More than 3 is 0.4912-0.2541, which is exactly 3=0.2371
Question 1195517: a die is thrown six times.what is the probability of getting exactly 4 six...
Two dice are rolled together. draw the sample space and find the probability that the sum of the scores of the dice is divided by 3
please any WhatsApp group here is my WhatsApp contact+2349024648165
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! Binomial distribution with 6C4 (1/6)^4*(5/6)^2=0.0080
The outcomes are 3, 6, 9, 12
Probability of a 3 is 2/36, 2/1 or 1/2
Probability of a 6 is 5/36 (4/2, 2/4, 3/3, 5/1,1/5)
Probability of a 9 is 4/36 (4/5, 5/4,6/3,3/6)
Probability of a 12 is 1/36
That sum is 12/36 or 1/3.
Question 1194599: Let X be a random variable having a binomial distribution with parameters n=25 and p=0.2 evaluate P[𝑋<𝜇𝑥−2𝜎𝑥]
Answer by reviewermath(1029)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let X be a random variable having a binomial distribution with parameters n=25 and p=0.2 evaluate P[𝑋<𝜇𝑥−2𝜎𝑥]
Solution:
The mean and variance of Binomial(n, p) are E(X) =np and Var(X) = np(1-p), respectively.
The mean of X is E(X)= np = 25(0.2) = 5 and the variance is Var(X)= np(1-p) = 25(0.2)(0.8) = 4.
The standard deviation of X is the square root of the variance which is 2.
We want to find P[𝑋<𝜇𝑥−2𝜎𝑥] = P[𝑋< 5 - 2(2)] = P(X < 1) = P(X = 0) =  = 0.003777893 = 0.003777893
If you have clarifications, just email me (reviewermath yahoo). I can tutor you on the whiteboard.
Question 1195030: Four women’s college basketball teams are participating in a single-elimination holiday basketball tournament. If one team is favored in its semifinal match by odds of "1.70 to 1.30" and another squad is favored in its contest by odds of "2.60 to 1.40", what is the probability that:
a. Both favored teams win their games? (Round your answer to 2 decimal places.)
b. Neither favored team wins its game? (Round your answer to 4 decimal places.)
c. At least one of the favored teams wins its game? (Round your answer to 4 decimal places.)
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The odds in favor of the first team's winning being 1.70:1.30 means the probability of its winning is 1.70/(1.70+1.30)=1.70/3.00 = 17/30. Then the probability that that team loses is 13/30.
Similarly, for the second team, the odds in favor of winning of 2.60:1.40 means its probability of winning is 26/40=13/20 and its probability of losing is 7/20.
Then....
a. Both win:
(17/30)(13/20)=221/600
b. Neither wins:
(13/30)(7/20) = 91/600
c. At least one wins:
1 minus the probability that neither wins: 1 - 91/600 = 509/600
Question 1194557: 1. According to one survey in India, 75% of Instagram users love REELS. Suppose that 25
Instagram users (randomly selected) have been approached in the university located in vile
parle. They have been asked about their status of like/ dislike the Instagram- REELS.
a) What is the probability that Exactly 15 of them would agree with the claim (or said they
love Insta-REELS)?
b) What is the probability that Exactly 20 of them would agree with the claim (or said they
love Insta-REELS)?
2. ‘Bhartdarshan’ is an Internet-based travel agency wherein customers can see videos of the
cities they plan to visit. The number of hits daily is a normally distributed random variable
with a mean of 10,000 and a standard deviation of 2,400.
a. What is the probability of getting more than 12,000 hits?
b. What is the probability of getting fewer than 9,000 hits?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
D U P L I C A T E
See my response under this link
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1194559.html
Question 1193467: Research finds that of the students entering a degree program, 90% will successfully complete it. In 2018, 15 students commenced the course. Calculate the probability that:
I) all 15 students will successfully complete the course.
II) only one student fails.
III) no more than two students fail.
I) at least two students fail.
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1193100: A survey shows that about 70 % of those over the age of 65 years old are in danger of catching COVID-19. If 7 persons over the age of 65 are randomly selected, answer the following questions:
A) What is the probability exactly 4 of the 7 have COVID-19?
b.) What is the probability at most 1 of the 7 has COVID-19?
c.) What is the probability at least 2 of the 7 have COVID-19?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A survey shows that about 70 % of those over the age of 65 years old
are in danger of catching COVID-19.
If 7 persons over the age of 65 are randomly selected, answer the following questions:
a) What is the probability exactly 4 of the 7 have COVID-19?
b) What is the probability at most 1 of the 7 has COVID-19?
c) What is the probability at least 2 of the 7 have COVID-19?
~~~~~~~~~~~~~
These are standard problems on binomial distribution.
(a) - number of trials n = 7;
- number of success trials k = 4;
- Probability of success on a single trial p = 0.7.
P = 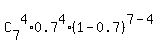 = = 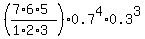 = 0.2269 (rounded). ANSWER
(b) - number of trials n = 7;
- number of success trials k <= 1; (k = 0, 1)
- Probability of success on a single trial p = 0.7.
Use online free of charge calculator https://stattrek.com/online-calculator/binomial.aspx
P = P(n=7; k<=1; p=0.7) = 0.003791 (rounded). ANSWER
(c) - number of trials n = 7;
- number of success trials k >= 2; (k = 2,3,4,5,6,7)
- Probability of success on a single trial p = 0.7.
You may use online free of charge calculator https://stattrek.com/online-calculator/binomial.aspx
P = P(n=7; k>=2; p=0.7) = 0.9962 (rounded),
or simply notice that this probability is the complement to that found in part (b)
P = 1 - 0.003791 = 0.9962 (the same value). ANSWER = 0.2269 (rounded). ANSWER
(b) - number of trials n = 7;
- number of success trials k <= 1; (k = 0, 1)
- Probability of success on a single trial p = 0.7.
Use online free of charge calculator https://stattrek.com/online-calculator/binomial.aspx
P = P(n=7; k<=1; p=0.7) = 0.003791 (rounded). ANSWER
(c) - number of trials n = 7;
- number of success trials k >= 2; (k = 2,3,4,5,6,7)
- Probability of success on a single trial p = 0.7.
You may use online free of charge calculator https://stattrek.com/online-calculator/binomial.aspx
P = P(n=7; k>=2; p=0.7) = 0.9962 (rounded),
or simply notice that this probability is the complement to that found in part (b)
P = 1 - 0.003791 = 0.9962 (the same value). ANSWER
Solved.
------------------------
If you want to see many similar or different solved problems on binomial distribution probability, look into the lessons
- Simple and simplest probability problems on Binomial distribution
- Typical binomial distribution probability problems
- How to calculate Binomial probabilities with Technology (using MS Excel)
- Solving problems on Binomial distribution with Technology (using MS Excel)
- Solving problems on Binomial distribution with Technology (using online solver)
in this site.
After reading these lessons, you will be able to solve such problems on your own,
which is your PRIMARY MAJOR GOAL visiting this forum (I believe).
Question 1192953: a firm which conducts consumer surveys by mail has found that 30 percent of those families receiving a questionnaire will return it. in a survey of 10 families, what is the probability that (1) exactly five families will return the questionnaire.(ii) between 3 to 5 five families (inclusive) will return the questionnaire (iii) exactly 10 will return the questionnairo?
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! exactly 10 will return is 0.3^10=0.0000059 or 5.9 x 10^(-6)
-
5 families is 10C5*0.3^5*0.7^5=252*0.3^5*0.7^5=0.1029
-
4 families is 10C4=210*0.3^4*0.7^6=0.2001
-
3 families is 10C3=120*0.3^3*0.7^7=0.2668
Total of those three is 0.5698.
Question 1191469: There are 5 coins in a bag: 3 weighted coins with Pr[H]=8/9 and 2 fair coins. One is chosen at random and flipped 180 times. What is the expected number of H flipped?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If a fair coin is chosen and flipped 180 times, the expected number of heads will be 180(1/2) = 90.
If a weighted coin is chosen and flipped 180 times, the expected number of heads will be 180(8/9) = 160.
The probability that a fair coin is selected is 2/5; the probability that a weighted coin is selected is 3/5.
The expected number of heads in the described experiment is then
(2/5)(90)+(3/5)(160) = 36+96 = 132
ANSWER: 132
Question 1191269: Mr. Keller filled out a bracket for the NCAA National Tournament. Based on his knowledge of college basketball, he has a 0.58 probability of guessing any one game correctly.
What is the probability Mr. Keller will pick all 32 of the first round games correctly?
What is the probability Mr. Keller will pick exactly 4 games correctly in the first round?
What is the probability Mr. Keller will pick exactly 22 games incorrectly in the first round?
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! a. This is 0.58^32=2.7 x10^(-8)
b. This is 32C4*0.58^4*0.42^28 by the binomial formula=1.15*10^(-7)
c. This issue 32C10*0.58^10*0.42^22=0.0814
The mean is 32*0.58=18.56 games correctly
The variance is 18.56*0.42=7.80
sd is sqrt(V)=2.80
Question 1191230: Paula is building a rectangular patio. It will
have a square flower bed in the middle. The
rest will have paving stones. The patio will
have a length of Ax and a width of 3.1x. The
area of the flower bed will be 3.52. What
area of the patio will need paving stones?
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution and the answer to this problem are in one line
the area of the patio which should be paved is (Ax)*(3.1x) - 3.52 = 3.1Ax^2 - 3.52. ANSWER
The many-word reasoning in the post by @Theo, his solution and his answer are incorrect and irrelevant.
Ignore his post, for the peace in your mind.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! capital A is usually used to represent area.
in this case, i think it might represent the area of the flower bed.
assuming i'm right, i think the solution to this problem might be as follows:
length of the patio is Ax.
width of the patio is 3.1x.
length and width of the flower bed is x.
the area of the flower bed is 3.52 which is equal to x^2.
this makes x = sqrt(3.52).
length of the patio is Ax = 3.52x
width of the patio is 3.1x.
area of the patio is 3.52x * 3.1x = 10.912x^2
since x = sqrt(3.52), then area of the patio is equal to 10.912 * x^2 = 10.912 * 3.52 = 38.41024.
the area of the patio that will need paving stones will be 38.41024 minus 3.52 = 34.89024.
that's what i think if my assumption about the value of A is correct.
if i did not know the value of A, then i would have done the following:
area of the patio = Ax * 3.1x = 3.1Ax^2
area of the flower bed = 3.52 = x^2
area of the patio becomes 3.1 * A * 3.52 = 10.912A
area of the patio that needs to be paved would be equal to 10.912A - 3.52.
i would not know the value of A and could not make any assumptions about its value.
my assumption that A is equal to the area of the flower bed gave it a value.
if i was right, then your answer would be that the area of the patio that will need paving stones will be 38.41024 minus 3.52 = 34.89024.
if i was wrong, then i would have to stick with the area of the patio that will need paving stones will be equal to 10.912A - 3.52.
Question 1191236: Paula is building a rectangular patio. It will
have a square flower bed in the middle. The
rest will have paving stones. The patio will
have a length of 4x and a width of 3.1x. The
area of the flower bed will be 3.52. What
area of the patio will need paving stones?
Found 3 solutions by ikleyn, MathLover1, ankor@dixie-net.com:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The " solution " by @MathLover11 is absolutely wrong.
Do not use it, since it is totally incorrect.
Use the correct solution by tutor @ankor@dixie-net.com.
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Paula is building a rectangular patio.
It will have a square flower bed in the middle.
The rest will have paving stones.
The patio will have a length of 4x and a width of 3.1x.
Find the area of the patio
4x * 3.1x = 12.4x^2
:
The area of the flower bed will be 3.52.
What area of the patio will need paving stones?
12.4x^2 - 3.52 = paving stone area
Question 1189096: The mean birth weight for Ethiopian babies is μ =3.1 kg with sd (σ=0.5 kg)
A) What weight values encompass the 95% newborns?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the mean is 3.1 kg and the standard deviation is .5 kg.
with a two tailed confidence interval of 95%, the critical z-score will be plus or minus 1.96
that leave a 2.5% tail on both ends of the confidence interval that are outside the confidence interval.
the z-score formula is:
z = (x - m) / s
in this case:
z is the z-score
x is the sample mean
m is the population mean
s is the population standard deviation
you get 1.96 = (x - 3.1) / .5 and -1.96 = (x - 3.1) / .5
when z = 1.96, solve for x to get x = 1.96 * .5 + 3.1 = 4.08.
when z = -1.96, solve for x to get x = -1.96 * .5 + 3.1 = 2.12
at 95% confidence interval, the weight of babies will be between 2.12 and 4.08 kg.
what they says is that, approximately 95% of the samples taken will have a sample mean between 2.12 and 4.08 kg.
here's what it looks like on a graph.
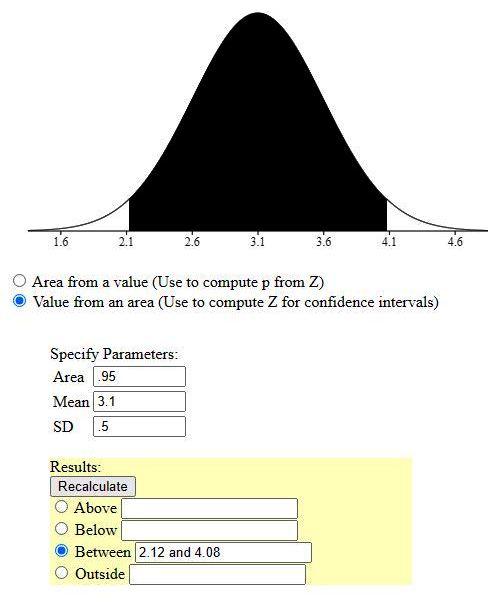
Question 1189004: Biostatistics Exercise
1.
2.
3.
5.
6.
8.
9.
10.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One and ONLY ONE problem/question per post.
It is the RULE, the POLICY and the REQUIREMENT of this forum.
It is written in this page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you post your problems.
It is assumed that you read these rules before posting.
It is also assumed that you do understand what is written in that page and follow the rules.
Those who violate them, work against their own interests.
*******************************************************************
So P L E A S E post your problems S E P A R A T E L Y (!)
*******************************************************************
Question 1186589: Determine the probabilities of having
(a) at least 1 girl
(a) at least 1 girl and 1 boy in a family of 4 children, assuming equal probability of male and female birth
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Determine the probabilities of having
(a) at least 1 girl
(b) at least 1 girl and 1 boy in a family of 4 children, assuming equal probability of male and female birth
~~~~~~~~~~~~~~~
(a) With 4 children in a family, there are, in total, 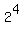 = 16 possible different configurations of boys/girls.
Of them, there is only one "unfavorable" configuration, when all the children are boys.
All other 15 configurations have at least one girl.
So, there are 16 total configurations and of them, there are 15 favorable, having at least one girl.
THEREFORE, the probability to have at least one girl in a family with 4 children
is = 16 possible different configurations of boys/girls.
Of them, there is only one "unfavorable" configuration, when all the children are boys.
All other 15 configurations have at least one girl.
So, there are 16 total configurations and of them, there are 15 favorable, having at least one girl.
THEREFORE, the probability to have at least one girl in a family with 4 children
is  . ANSWER
(b) Again, there are 16 possible different configurations, in all.
Of them, "unfavorable" are only 2 (two), having all 4 boys OR having all 4 girls.
The rest 16-2 = 14 configurations are "favorable" : they have at least one boy and at least one girl.
THEREFORE, the probability to have at least one girl AND at least one boy in a family with 4 children
is . ANSWER
(b) Again, there are 16 possible different configurations, in all.
Of them, "unfavorable" are only 2 (two), having all 4 boys OR having all 4 girls.
The rest 16-2 = 14 configurations are "favorable" : they have at least one boy and at least one girl.
THEREFORE, the probability to have at least one girl AND at least one boy in a family with 4 children
is 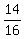 = =  . ANSWER . ANSWER
Solved and thoroughly explained.
Question 1185040: A grocery store counts the number of customers who arrive during an hour. The average over a year is 27 customers per hour. Assume the arrival of customers follows a Poisson distribution. (It usually does.)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A grocery store counts the number of customers who arrive during an hour. The average over a year is 27 customers per hour.
Assume the arrival of customers follows a Poisson distribution. (It usually does.)
~~~~~~~~~~~~~~~~~~
Thanks for sharing this info with us, the tutors . . .
What is your question ( in case if you have it . . . ) ?
Or you think it is unnecessary to disclose it to us ?
Next time, it may happen that your message, posted with no question, you will find in the TRASH SECTION.
The BOTTOM LINE is : when you communicate with tutors, be accurate and polite.
If you don't know what to ask, do not post to this forum and do not disturb the tutors without necessity.
Have a nice day / night . . .
Question 1183498: A hunter bring down 75% of a rabbit he shoot at .what is the probability that at least 3 of the next five rabbit shot will escape
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1182888: A retailer’s survey learned that 35% of all people aged 35 to 54 do more than half
of their shopping online. Find the probability that 20 or fewer out of 46 randomly
selected people aged 35 to 54 do more than half of their shopping online.
1. Determine the binomial parameters, n and p, giving values and descriptions.
2. Determine the question being asked, P(x “=, <, <, >, or >” a number), that is, write the
question symbolically as illustrated in lecture videos (and page 2 of this lab 3 packet).
3. Determine the calculator command needed to solve the problem.
(See separate sheet on using calculator to solve binomial problems.)
4. Use the calculator to find the solution to the binomial probability;
round answers to 4 decimal places.
5. Write your answer in a sentence in terms of the application
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Cutting and pasting your entire assignment, with nothing else in your post, does a couple of things....
(1) It strongly suggests you simply want us to do your work for you -- which is not the purpose of this forum.
(2) It tells us you aren't even putting in any effort to make the post usable to us; we don't have access to your lecture videos, lab packets, or the sheet on using a calculator to solve binomial probability problems.
|
|