SOLUTION: FIND THE SUM OF TWO DIGIT NUMBERS WHICH BEING DIVIDED BY 4 LEAVE A REMAINDER OF 1. (ANS-1210)

Algebra ->  Average -> SOLUTION: FIND THE SUM OF TWO DIGIT NUMBERS WHICH BEING DIVIDED BY 4 LEAVE A REMAINDER OF 1. (ANS-1210)      Log On


   

Question 866321: FIND THE SUM OF TWO DIGIT NUMBERS WHICH BEING DIVIDED BY 4 LEAVE A REMAINDER OF 1.
(ANS-1210)
Found 2 solutions by htmentor, MathLover1:
Answer by htmentor(1343) About Me  (Show Source):
You can put this solution on YOUR website!
The sequence of numbers divisible by 4, with a remainder of 1 are 5,9,13,17,21,...
The general formula for the nth term of this sequence is a_n = 4n + 1
The sum of the first n terms of an arithmetic sequence, S_n = (n/2)*(a_1 + a_n)
n=24 gives the largest two digit number, 97.
S_24 = (24/2)(5+97) = 1224. But the two digit numbers start with 13, so we need to subtract 5+9=14 from this sum
Ans: 1210

Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
the number is of the form 4x%2B1 by definition where x is a natural number
first such 2 digit number is 4%2A3%2B1=13+
last such 2 digit number is 4%2A24%2B1=97+

this is an arithmetic progression with common difference 4
so, we have 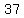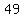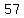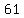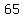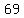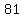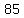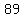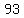13,17,21,25,29,33,37%7D%7D%5D%2C%7B%7B%7B41,45,49,53,57,61,65,69,73,77,81,85,89,93,97
the sum is given by sum=%28n%2F2%29%282a%2B%28n-1%29%2Ad%29+
n is the number of terms, a is the first number, d is the common difference
n=%2897-13%29%2F4%2B1=22+
a=13
d=4
sum=%2822%2F2%29%2A%282%2A13%2B21%2A4%29=+11%28110%29=1210+